初三数学教学测量与评价（三）

 

初三数学教学测量与评价（三）

（总分130分，答卷时间120分）

一、选择题（本大题共12小题，1—8题每题2分，9—12题每题3分，共28分。

下列各题的四个结论中，只有一个是正确的。请将正确的答案的字母代号填在

下面的表格内。）

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案

1. 的相反数是(　　　 )

 A．-5　　　　 B.5　　　　　　 C.　　　　　　  D.

2. 下列图形中∠1和∠2为对顶角的是(　　　 )

D.

C.

B.

A.

 

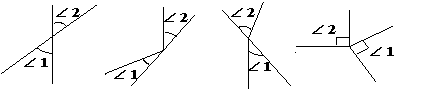
3. 下列计算正确的是(　　　　)

A．　 B.　 C.　 D.

4. 南京市政府宣布从2006年7月1日起至2008年底前,全市130万用户都看上

有线数字电视.130万户用科学记数法记为(　　　 )

A．130×10⁴ 户　　B.1.30×10⁴　户　 C.1.30×10⁶ 户　D.1.30×10⁵ 户

5.式子中,的取值范围是(　　　 )

A．　　  B.　　　C.　　　　　D.

6.如图,将两块完全相同的30°角的直角三角板恰好

拼在△ABC的内部,那么下列结论①BD=AD ②∠ABE=15°

③△BDE与△ACD的相似比为1

 正确的有(　　　 )

A．0个　　　　B. 1个　　　　 C.　2个　　  D. 3个

7. 分式方程的增根是(　　　　)

A. 　　　B.　　　　C.　　　D.

8.已知抛物线,则其顶点坐标为(　　　　)

A．(-2,-3)　　　B.(4,1)　　　C.(2,-3)　　 D.(-2,3)

9.下列命题中,真命题是(　　　　)

A．直角一定不是对顶角

  B．相等的圆周角所对的弧相等

  C．平分弦的直径垂直于弦

D. 90°的圆周角所对的弧的度数是180°

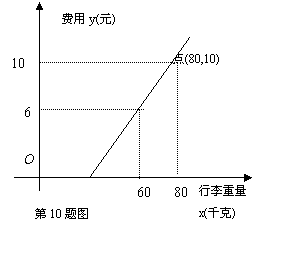
10.某地长途汽车客运公司规定旅客可随身

携带一定重量的行李，如果超过规定，

则需要购行李票，行李票价（元）

是行李重量（千克）的一次函数，

其图象如图所示;那么旅客最多可免

费携带行李(　　　　)

A.30千克　　 B.45千克　　　C.60千克　　 D.15千克

11.已知 ,则（　　　　）

A．　　  B.　　  C.　　　D.

12.式子是一个整数的完全平方，则整数的值有（　　　　）

A．4个　　　 B.6个　　　　 C.8个　　　　 D.无数个

二、填空题：（本大题共6小题，每小题3分，共18分）

13.分解因式　　　　　　　　　　　  .

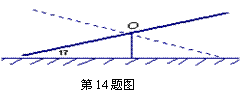14.如图, 跷跷板两端等长,一端触地面时

与地面所成角度是17°, 那么跷跷板绕着

支点O旋转的最大角度是　　　　　　  .

15.一个圆柱形有盖铁皮饼干包装盒

高7cm,底面圆半径12cm,则制成

盒子的表面的铁皮至少需要　　　　　　　  cm².

(结果保留π)

16. 某花木园计划在园中栽96棵桂花树,开工后每天比原计划多栽2棵,结果提前

4天完成.设原计划每天栽棵,得到的分式方程是　　　　　　　　　　　　　　　 .

17.函数的图象与轴只有一个交点,则的值是　　　　　　　　　　 .

18.关于的方程的两根是一个Rt△的两锐角的正弦值,且,则的平方根是　　　　　　　　 .

二、解答题（本大题共10题，共84分）

19.（本题有两小题，共10分）

　（1）计算：

（2）先化简再求值：，其中

20.（本小题6分）

解不等式组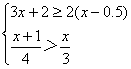：,并把解集在数轴上表示出来.

　

21.（本小题6分）

　已知:△ABC及BC边上的中线AM

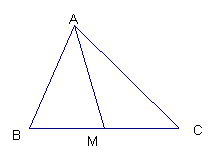　 (1)求作: △ABC关于点M的中心对称图形;

　 (2)当△ABC是什么三角形时, △ABC关于点

M的中心对称图形也是它的轴对称图形.

22.（本小题7分）

某校初三（1）班、（2）班各有49名学生，两班在一次数学测验中的成绩统计如下表：

班级	平均分	众数	中位数	标准差
初三（1）	79	70	87	19.8
初三（2）	79	70	79	5.2

(1)　请你对下面的一段话给予简要分析:

　　初三（1）班的小刚回家对妈妈说:“昨天的数学测验,全班平均79分,得70分的人最多,我得了85分,在班里可算上游了!”

(2)　请你根据表中数据,对这两个班的测验情况进行简要分析,并提出教学建议.

23.(本小题6分)

等腰梯形ABCD中，AD∥BC，AB=AD=CD=4，∠D=120°，

（1）　　　 求梯形的高AH；

（2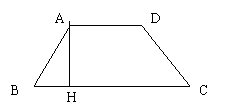）　　　 求梯形ABCD的面积S.

24. (本小题8分)

一个学生上学乘公交车有三种方式①每次上车直接投币1元;②先用20元购买学生卡,卡上再存足钱,每次上车刷卡0.5元,每月最多刷卡60次,以后每次刷卡0.8元;③先用20元购买成人卡,卡上再存足钱,每次上车刷卡0.8元;

(1)　若这名学生一月中乘车次数为30次,分别求出三种方式

一个月的总费用(包括购卡费用),并判断哪种方式便宜;

(2)　若这名学生每月乘车次数为次,求出方式②的一个月的总费用(元)关于的

函数关系式.(总费用包括够卡费用)

 

25．（本题9分）

已知:如图,在矩形ABCD中,E为 AD中点,EF⊥EC交AB于F,连结FC.(AB＞AE)

(1)　请你找出一对相似三角形,并证明它们相似;

(2)　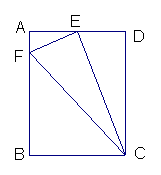请你找出哪一条线段是线段CF与CD的比例中项,

并证明你的结论.

26．（本小题10分）

已知:如图, Rt△中, ∠,点在边上,以为圆心、为半径的圆与相切于点，交于点.

(1)求证: 是⊙的切线;

　　(2)求证: ∥

　　(3)若⊙的半径为2,求的长.

27．(本小题10分)

　　　已知抛物线开口向下,与轴交于A(,0)和B(,0)两点,其中＜.

(1)　求的取值范围;

(2)　若求抛物线的解析式,并在给出的直角坐标系中画出这条抛物线;

(3)　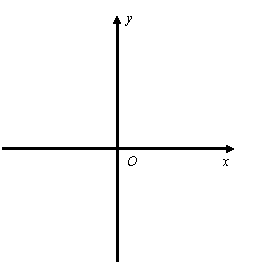设(2)中的抛物线的顶点为C,延长CA交轴于点D.在轴上是否存在点P,使以P、O、B为顶点的三角形与△BCD相似？若存在，求出P点的坐标；若不存在，请说明理由.

28.(本小题12分)

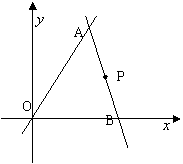
如图,直线经过点P(5,3),且分别与已知直线交于点A、与轴交于点B,设点A的横坐标为m(m＞1且m≠5)

(1)用含m的代数式表示;

(2)写出△AOB的面积S关于m的函数解析式;

(3)在直线上是否存在点A,使得△AOB

的面积最小?若存在,请求出点A的坐标和

S的最小值;若不存在,请说明理由.