初三数学开放题、探索题选编（二）
1. 同学们知道:只有两边和一角对应相等的两个三角形不一定相等.你如何处理和安排这三个条件,使这两个三角形全等,请你依照方案(1),写出方案(2)、(3)、(4).
解：设有两边和一角对应相等的两个三角形. 方案（1）：若这角的对边恰好是这两边中的大边，则这两个三角形全等；
2.
一副三角板由一个等腰直角三角形和一个含30
的直角三角形组成,利用这副三角板构成一个含有15角的方法较多,请你画出其中两种不同构成的示意图,并在图上标出必要的标柱,不写作法.
3. 在四边形ABCD中,M,N,P,Q分别是四边形各边AB、BC、CD、DA的中点，当四边形ABCD满足条件 时，四边形MNPQ为矩形；
4.
|
 |
(取BC或AD中点P,或过对角线的交点,作AB的平行线交BC或AD于点P).
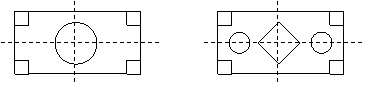
5. 某居民小区搞绿化,要在一块矩形空地上建花坛,现征集设计方案,要求设计的图案由圆和正方形组成(圆和正方形的个数不限)并且使整个矩形场地成轴对称图形,请在矩形中画出你设计的方案.(北京考题)
 |
6.
关于
的方程
，是否存在负数
，使方程的两个实数根的倒数和为
？若存在，求出满足条件的负数值，若不存在，请说明理由？
7. 研究下列各式，你会发现什么规律？
，
，
，
………
请将你找出的规律用公式表示出来 ；
8. 1.判断下列各式是否成立,你认为成立的,请在括号内打“√”，不成立的请在括号内打“×”
（1）
（ ） （2）
（ ）
（3）
（ ） （4）
（ ）
2.你判断完以上各题之后，发现什么规律？请用含有n的式子将规律表示出来，并注明n的取值范围；(
)
9. 下列每个图是由若干盆花组成的形如三角形的图案,每条边(包括两个顶点)有n(n>1)盆花,每个图案的花盆的总数是S
 | |||||
 |  | ||||
n=2 ,S=3 n=3, S=6 n=4, S=9
按此规律推断,S与n的关系式为 ; (3n-3)
10.
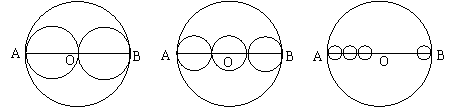
如图,AB是⊙O的直径,把线段AB分成几条相等的线段,以每条线段为直径分别画小圆,设AB=
,那么⊙O的周长为
,试计算
(1)
把AB分成两条相等的线段,每个小圆的周长
(2)
把AB分成三条相等的线段,每个小圆的周长
;
(3)
把AB分成四条相等的线段,每个小圆的周长
=
;
……
(4)
把AB分成n条相等的线段,每个小圆的周长
=
;
 |
结论:把大圆的直径分成n条线段,以每条线段为直径画小,那么每个小圆周长是 大圆周长的 ;
请仿照上面的探索方法和步骤,计算推导出每个小圆面积和大圆面积的关系.
(答案:
(
分别为n等分直径的小圆面积和大圆面积)
11.
（归纳猜想）已知一个半径为20cm的圆，作该圆内接钝角三角形，求这个钝角三角形面积的取值范围。（0<S<400）
12. （分类讨论）有一个三角形ABC，现要用一个圆形纸片来覆盖它，尽可能使纸片最小，请说明圆形纸片如何确定。