初三数学模拟试卷(二)
一、选择题: 本大题共12小题；每小题3分，共36分，在每小题给出的四个选项中，只有一项是符合题目要求的．
1．下列二次根式中与
是同类二次根式的是 （ ）
A．
B．
C．
D．
2.不等式组的解在数轴上表示为（ ）
3．面积为2的△ABC，一边长为x，这边上的高为y，则y与x的变化规律用图象表示大致是 （ ）
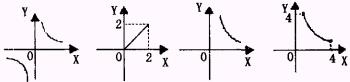
ABCD
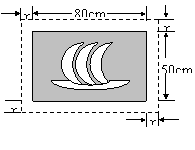4. 在一幅长80cm，宽50cm的矩形风景画的四周镶一条金色纸边，制成一幅矩形挂图，如图所示，如果要使整个挂图的面积是5400cm2，设金色纸边的宽为xcm，那么x满足的方程是【 】
A．x2+130x-1400=0 B．x2+65x-350=0
C．x2-130x-1400=0 D．x2-65x-350=0
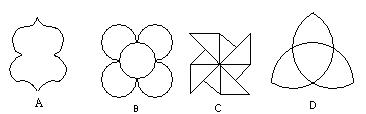
5、下列图案中，有且只有三条对称轴的是（ ）
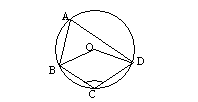
6. 如图，四边形ABCD内接于⊙O，若
，则
（ ）
A. 
B. 
C.
D. 
7. 设M表示直角三角形，N表示等腰三角形，P表示等边三角形，Q表示等腰直角三角形，则下列四个图中，能表示它们之间关系的是（ ）．
（A）
（B）
（C）
（D）
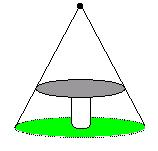8、如图：这是圆桌正上方的灯泡（看作一个点）发出的光线照射桌面后，在地面上形成阴影（圆形）的示意图，已知桌面的直径为1.2米，桌面距离地面1米，若灯泡距离地面3米，则地面上阴影部分的面积为（ ）
A、
平方米
B、
平方米
C、
平方米
D、
平方米
9.火车票上的车次号有两个意义，一是数字越小表示车速越快，1~98次为特快列车，101~198次为直快列车，301~389次为普快列车，401~598次为普客列车；二是单数与双数表示不同的行驶方向，其中单数表示从北京开出，双数表示开往北京.根据以上规定，杭州开往北京的某一直快列车的车次号可能是（ ）
（A）20 （B）119 （C）120 （D）319
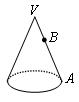10.如图，点B在圆锥母线VA上，且VB=
.过点B作平行于底面的平面截得一个小圆锥，若小圆锥的侧面积为S1，原圆锥的侧面积为S，则下列判断中正确的是（ ）
（A）
（B）
（C）
（D）
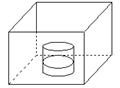
11、如图：向放在水槽底部的烧杯注水（流量一定），注满烧杯后，继续注水，直至注满水槽，水槽中水面上升高度
与注水时间
之间的函数关系大致是下列图象中的（ ）
12.甲、乙、丙三位同学进行立定跳远比赛，每人轮流跳一次称为一轮，每轮按名次从高到低分别得3分、2分、1分（没有并列名次）.他们一共进行了五轮比赛，结果甲共得14分；乙第一轮得3分，第二轮得1分，且总分最低.那么丙得到的分数是（ ）
（A）8分 （B）9分 （C）10分 （D）11分
二、填空:本大题共8小题；每小题4分，共32分．把答案填写在题中横线上．
13. 分解因式:x3y2-4x= .
14. 计算：
=
.
15.
若反比例函数y=
经过点（-1，2），则一次函数y=-kx+2的图象一定不经过第
象限.
16、乘火车从A站出发，沿途经过3个车站方可到达B站，那么在A、B两站之间需要安排不同的车票 种。
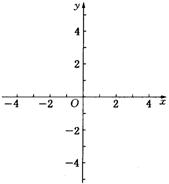
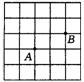17. 已知右边方格纸中的每个小方格是边长为1的正方形，A、B两点在小方格的顶点上，位置如图所示．请在小方格的顶点上确定一点C，连结AB、AC、BC，使△ABC的面积为2个平方单位．
18.
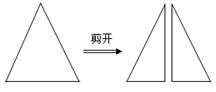如图，有一腰长为5cm，底边长为4cm的等腰三角形纸片，沿着底边上的中线将纸片剪开，得到两个全等的直角三角形纸片，用这两个直角三角形纸片拼成的平面图形中有
_____________个不同的四边形.
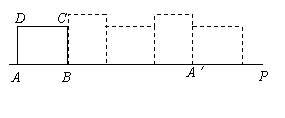
19.已知矩形ABCD的长AB=4，宽AD=3，按如图放置在直线AP上，然后不滑动地转动，当它转动一周时（A→A′），顶点A所经过的路线长等于 .
20. 用黑白两种颜色的正六边形地面砖按如下所示的规律，拼成若干个图案：
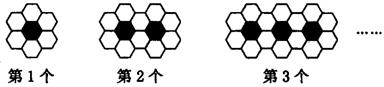
⑴ 第4个图案中有白色地面砖
块；
⑵ 第n个图案中有白色地面砖
块．
三、解答题：（本题共8个小题，共82分）
21. （本题满分8分）
解方程：
22. （本题8分）
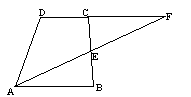
已知：如图，梯形ABCD中，
，E是BC的中点，直线AE交DC的延长线于点F。
（1）求证：
；
（2）若
，且BC=10，AB=12，求AF的长。
23.（本题满分8分）
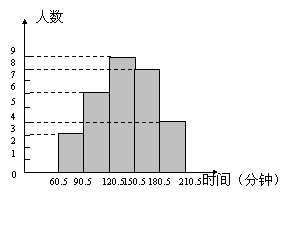
某研究性学习小组，为了了解本校初一学生一天中做家庭作业所用的大致时间（时间以整数记.单位：分钟），对本校的初一学生做了抽样调查，并把调查得到的所有数据（时间）进行整理，分成五个时间段，绘制成统计图（如图所示），请结合统计图中提供的信息，回答下列问题：
（1）这个研究性学习小组所抽取样本的容量是多少？
（2）在被调查的学生中，一天做家庭作业所用的大致时间超过120分钟（不包括120分钟）的人数占被调查学生总人数的百分之几？
（3）这次调查得到的所有数据的中位数落在了五个时间段中的哪一段内？
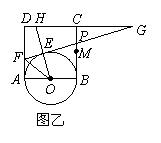
24.（本小题10分）已知动点P以每秒2cm的速度沿图甲的边框按从B→C→D→E→F→A的路径移动，相应的△ABP的面积S关于时间t的函数图象如图乙.若AB=6，试回答下列问题：
（1）图甲中BC的长是多少？
（2）图乙中的a是多少？
（3）图甲中的图形面积是多少？
（4）图乙中的b是多少？
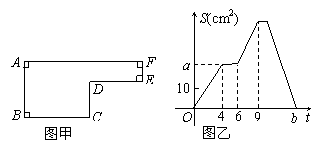
25. （本题满分10分） 有一长方形餐厅，长10米，宽7米，现只摆放两套同样大小的圆桌和椅子，一套圆桌和椅子占据的地面部分可看成半径为1．5米的圆形（如左下图所示）．在保证通道最狭窄处的宽度不小于0．5米的前提下，此餐厅内能否摆下三套或四套同样大小的圆桌和椅子呢？请在摆放三套或四套的两种方案中选取一种，在右下方 14×20方格纸内画出设计示意图．
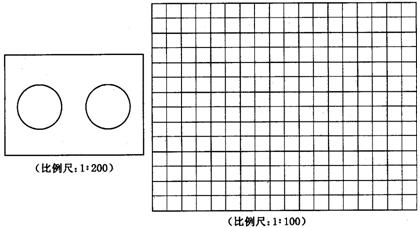
（提示：①画出的圆应符合比例要求；
②为了保证示意图的清晰，请你在有把握后才将设计方案正式画在方格纸上．
说明：正确地画出了符合要求的三个圆得5分，正确地画出了符合要求的四个圆得10分．）
26. （本题满分12分）抛物线的解析式 
满足四个条件：abc＝0；a＋b＋c＝3；ab＋bc＋ca＝－4； a＜b＜c．
⑴ 求这条抛物线的解析式；
⑵ 设该抛物线与x轴的两交点分别为A、B（A在B的左边），与y轴的交点为C，P是抛物线上第一象限内的点，AP交y轴于点D，OD＝1．5，试比较S△AOD与S△DPC的大小。
27.（本题12分）如图甲，正方形ABCD的边长为2，点M是BC的中点，P是线段MC上的一个动点（不运动至M，C），以AB为直径作⊙O，过点P作⊙O的切线交AD于点F，切点为E.
（1）求四边形CDFP的周长；
（2）请连结OF，OP，证明OF⊥OP；
（3）延长DC，FP相交于点G，连结OE并延长交直线DC于H（如图乙）.是否存在点P，
使△EFO∽△EHG（其对应关系是E←→E，F←→H，O←→G）？如果存在，试求此时
的BP的长；如果不存在，请说明理由.
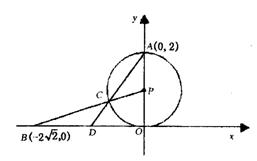28．（本题14分）已知：如图，⊙P与x轴相切于坐标原点O，点A（0，2）是⊙P与x轴的交点，点B（－2
，0）在x轴上，连结BP交⊙P于点C，连结AC并延长交际x轴于点D．
（1）求线段BC的长；
（2）求直线AC的函数解析式；
（3）当点B在x轴上移动时，是否存在点B，使△BOP相似于△AOD？若存在，求出符合条件的点的坐标；若不存在，说明理由．