初三数学模拟试卷(三)
一、选择题: 本大题共12小题；每小题3分，共36分，在每小题给出的四个选项中，只有一项是符合题目要求的．
1、下列实数
，sin30°，0.1414，
中，无理数的个数是
A、1个 B、2个 C、3个 D、4个
2．化简
的结果是 （ ）
A．
B．
C．
D．
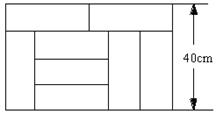
3、如图：用8块相同的长方形地砖拼成一个矩形，则每个长方形地砖的面积是（ ）
A、200cm2 B、300cm2
C、600cm2 D、2400cm2
4．（针孔成像问题）根据图中尺寸（AB//A′B′），那么物像长y(A′B′的长)与物长x（AB
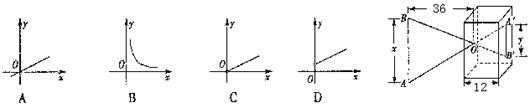的长）之间函数关系的图象大致是 （ ）
5．
等于 （ ）
A．
B．
C．
D．
6、小强拿了张正方形的纸如图（1），沿虚线对折一次如图（2），再对折一次得图（3），然后用剪刀沿图（3）中的虚线（虚线与底边平行）剪去一个角，再打开后的形状应是( )
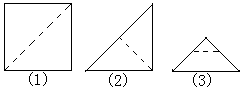
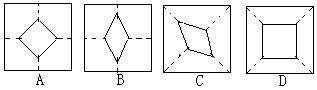
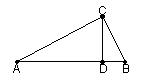
7、如图，在Rt△ABC中，∠C=90°，CD⊥AB，垂足为D，AD=8，DB=2，则CD的长为( )
A、4 B、16 C、2
D、4
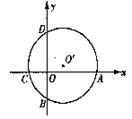8．如图，在平面直角坐标系中，⊙O′与两坐标轴分别交于A、B、C、D四点. 已知：A（6，0），B（0，－3），C（－2，0），则点D的坐标是 （ ）
A．（0，2） B．（0，3）C．（0，4） D．（0，5）
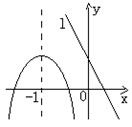9、已知抛物线和直线ι在同一直角坐标系中的图象如图所示，抛物线的对称轴为直线x=-1，P1(x1,y1)，P2(x2,y2)是抛物线上的点，P3(x3,y3)是直线ι上的点，且-1<x1<x2，x3<-1则y1,y2,y3的大小关系为( )
A. y1<y2<y3 B. y3<y1<y2
C. y3<y2<y1 D. y2<y1<y3
10. 某中学新科技馆铺设地面，已有正三角形形状的地砖，现打算购买另一种不同形状的正多边形地砖，与正三角形地砖在同一顶点处作平面镶嵌，则该学校不应该购买的地砖形状是
A、正方形 B、正六边形 C、正八边形 D、正十二边形
11、平面直角坐标系内，点A（
，
）一定不在（ ）
A、第一象限 B、第二象限
C、第三象限 D、第四象限
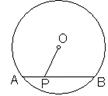
12、如图：⊙O的直径为10cm，弦AB为8cm，P是弦AB上一点，若OP的长为整数，则满足条件的点P有（ ）
A、2个 B、3个
C、4个 D、5个
二、填空:本大题共8小题；每小题4分，共32分．把答案填写在题中横线上．
13、生物学家发现一种病毒的直径约为0.000043米，用科学记数法表示为 米。
14、函数
中，自变量
的取值范围是
。
15．某班50名学生的年龄统计结果如下表所示：
| 年龄 | 13 | 14 | 15 | 16 |
| 人数 | 4 | 22 | 23 | 1 |
这个班学生年龄的众数是____，中位数是______．
16、矩形一个角的平分线分矩形一边为1cm和3cm两部分，则这个矩形的面积为 cm2。
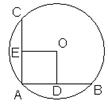
17、如图：在⊙O中，AB、AC为互相垂直且相等的两条弦，OD⊥AB，OE⊥AC，垂足分别为D、E，若AC＝2cm，则⊙O的半径为 cm。
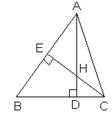
18、如图：△ABC中，AD⊥BC，CE⊥AB，垂足分别为D、E，AD、CE交于点H，请你添加一个适当的条件： ，使△AEH≌△CEB。
19、请根据所给方程
，联系生活实际，编写一道应用题。（要求题目完整，题意清楚，不要求解方程）＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿
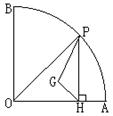20、如图，在半径为9，圆心角为90°的扇形OAB的弧AB上有一动点P，PH⊥OA，垂足为H，设G为△OPH的重心（三角形的三条中线的交点），当△PHG为等腰三角形时，PH的长为_______
三、解答题：（本题共8个小题，共82分）
21、（本小题8分）先化简，再求值：
，其中
22、（本小题8分）
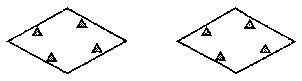
如图，菱形公园内有四个景点，请你用两种不同的方法，按下列要求设计成四个部分：⑴用直线分割；⑵每个部分内各有一个景点；⑶各部分的面积相等。（可用铅笔画，只要求画图正确，不写画法）
23、（本小题8分）某空军加油飞机接到命令，立即给另一架正在飞行的运输飞机进行空中加油，在加油过程中，设运输飞机的油箱余油量为
吨，加油飞机的加油油箱余油量为
吨，加油时间为
分钟，、与之间的函数图像如图所示，结合图像回答下列问题：
（1）加油飞机的加油油箱中装载了多少吨油？将这些油全部加给运输飞机需多少分钟？
（2）求加油过程中，运输飞机的余油量（吨）与时间（分钟）的函数关系式；
（3）运输飞机加完油后，以原速继续飞行，需10小时到达目的地，油料是否够用？说明理由。
24、（本小题10分）关于的方程
有两个不相等的实数根。
（1）求
的取值范围；
（2）是否存在实数，使方程的两个实数根的倒数和等于0 ？若存在，求出的值；若不存在，请说明理由。
25、（本小题10分）
已知：如图，在△ABC中，∠ABC＝90°，O是AB上一点，以O为圆心，OB为半径的圆与AB交于点E，与AC切于点D，连结DB、DE、OC。
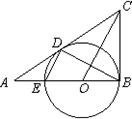⑴从图中找出一对相似三角形（不添加任何字母和辅助线），并证明你的结论；
⑵若AD＝2，AE＝1，求CD的长。
26、（本小题12分）为了保护环境，某企业决定购买10台污水处理设备，现有A、B两种型号的设备，其中每台的价格、月处理污水量及年消耗费如下表：
|
| A型 | B型 |
| 价 格（万元／台） | 12 | 10 |
| 处理污水量（吨／月） | 240 | 200 |
| 年消耗费（万元／台） | 1 | 1 |
经预算，该企业购买设备的资金不高于105万元。
（1）请你设计该企业有几种购买方案；
（2）若企业每月产生的污水量为2040吨，为了节约资金，应选择哪种购买方案；
（3）在第（2）问的条件下，若每台设备的使用年限为10年，污水厂处理污水费为每吨10元，请你计算，该企业自己处理污水与将污水排到污水厂处理相比较，10年节约资金多少万元？（注：企业处理污水的费用包括购买设备的资金和消耗费）
27、（本题满分12分）
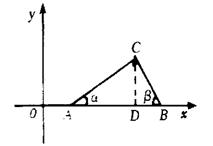如图，已知点A（tana，0），B（tanb，0）在x轴正半轴上，点A在点B的左边，a、b是以线段AB为 斜边、顶点C在x轴上方的Rt△ABC的两个锐角．
（1）若二次函数y＝－x2－
kx＋（2＋2k－k2）的图象经过A、B两点，求它的解析式；
（2）点C在（1）中求出的二次函数的图象上吗？请说明理由．
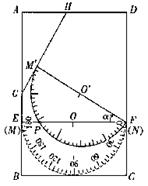
28．（本小题14分）如图，在矩形ABCD中，AB=3，AD=2，点E、F分别在AB、DC上，AE=DF=2.再把一块直径为2的量角器（圆心为O）放置在图形上，使其0°线MN与EF重合；若将量角器0°线上的端点N固定在点F上，再把量角器绕点F顺时针方向旋转∠α（0°<α
<90°）,此时量角器的半圆弧与EF相交于点P，设点P处量角器的读数为n°.
（1）用含n°的代数式表示∠α的大小；
（2）当n°等于多少时，线段PC与M′F平行？
|
