初三数学模拟试卷(四)

初三数学模拟试卷(四)

　　

一、选择题: 本大题共12小题；每小题3分，共36分，在每小题给出的四个选项中，只有一项是符合题目要求的．

1.　　　 若分式的值为零，则x等于

A、0　　　　　　　　　　　B、1　　　　　　　　　　 C、　　　　　　　　　D、－1

2. 将这三个数按从小到大的顺序排列，正确的结果是（　　  ）

  （A）＜＜（B）＜＜

（C）＜＜（D）＜＜

3. 抛物线y=2(x-3)²的顶点在(　　 )

　　　A、第一象限　　　　　B、第二象限　　　　　 C、x轴上　　　　　　　　 D、y轴上

4. 某种商品的进价为800元，出售时的标价为1200元，后来由于该商品积压，商店准备打折出售，但要保持利润率不低于5%，则至少可打（　　　 ）

（A）　　  6折（B）7折（C）8折（D）9折

5、等腰三角形一边长为4，一边长9，它的周长是

　　A、17　　　　　　 B、22　　　　　　 C、17或22　　　　D、13

6．下列图形中是中心对称图形的是

　　

7、△BAC中，AB＝5，AC＝12，BC＝13，以AC所在的直线为轴将△ABC旋转一周得一个几何体，这个几何体的表面积是

　　A、90π　　　　　 B、65π　　　　　 C、156π　　　　　D、300π

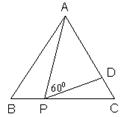
8、如图：在等边△ABC中，P为BC上一点，D为AC上一点，且

∠APD＝60⁰，BP＝1，CD＝，则△ABC的边长为（　　）

　　A、3　　　　　　  B、4　　　　　  C、5　　　　　  D、6

　　　　

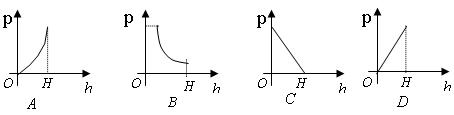
9、向高层建筑屋顶的水箱注水，水对水箱底部的压强p与水深h的函数关系的图象是（水箱能容纳的水的最大高度为H）。

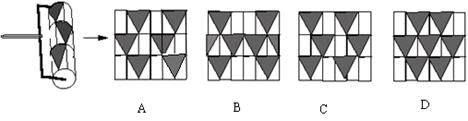
10．小明用如图所示的胶滚沿从左到右的方向将图案滚涂到墙上，下列给出的四个图案中，符合图示胶滚涂出的图案是（　　）

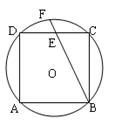11．如图，正方形ABCD内接于⊙O,E为 DC的中点，直线BE交⊙O于点F，若⊙O的半径为，则BF的长为　　　　（　　　）

A、　　B、　　C、　　D、　

12．计算机是将信息转换成二进制数进行处理的，二进制即“逢2进1”，如（1101）₂表示二进制数，将它转换成十进制形式是1×2³+1×2²+0×2¹+1×2⁰=13，　那么将二进制数（1111）₂转换成十进制形式是数　　 (　　 )

A．8　 B．15　C．20　 D．30

二、填空:本大题共8小题；每小题4分，共32分．把答案填写在题中横线上．

13．如图，是一个简单的数值运算程序，当输入x的值为－1时，则输出的数值为　　

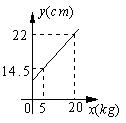14、分解因式：ax²-ay²=_______­­­_____________

15. 如图，如图，弹簧总长y（cm）与所挂物体质量x（kg）之间是一次函数关系，则该弹簧不挂物体时的长度为　　　　　  cm

16、已知梯形的中位线长为6，下底长为9，则该梯形上底的长为_______

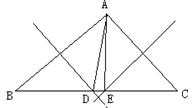
17、已知如图，在△ABC中，BC=8，AB的中垂线交BC于D，AC的中垂线交BC于E，则△ADE的周长等于_______

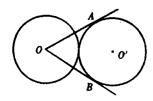18．如图，两个等圆⊙O和⊙O′外切，过⊙O作⊙O′的两条切线OA、OB、A、B、是切点，则∠AOB等于___________度.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

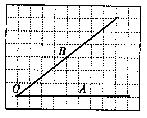19．如图，已知方格纸中的每个小方格都是相同的正方形，∠AOB画在方格纸上，请在小方格的顶点上标出一个点P，使点P落在∠AOB的平分线上.

20．欣赏下面的各等式：

3²+4²=5²

　　　　　　　　　 10²+11²⁺+12²=13²+14²

请写出下一个由7个连续正整数组成、前4个数的平方和等于后3个数的平方和的

等式为___________________________________.　

三、解答题：（本题共8个小题，共82分）

21. （本题满分8分）

　　用换元法解方程x²－3x－1＝．

22.（本小题8分）

已知：△ABC中，AB＝10

⑴如图①，若点D、E分别是AC、BC边的中点，求DE的长；

⑵如图②，若点A₁、A₂把AC边三等分，过A₁、A₂作AB边的平行线，分别交BC边于点B₁、B₂，求A₁B₁＋A₂B₂的值；

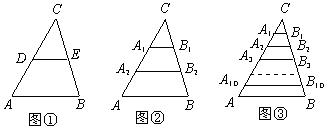⑶如图③，若点A₁、A₂、…、A₁₀把AC边十一等分，过各点作AB边的平行线，分别交BC边于点B₁、B₂、…、B₁₀。根据你所发现的规律，直接写出A₁B₁＋A₂B₂＋…＋A₁₀B₁₀的结果。

23．（本小题8分）某学校对初中毕业班经过初步比较后，决定从初三（1）、（4）、（8）班这三个班中推荐一个班为市级先进班集体的候选班.现对这三个班进行综合素质考评，下表是它们五项素质考评的得分表（以分为单位，每项满分为10分）.

班级	行为规范	学习成绩	校运动会	艺术获奖	劳动卫生
初三（1）班	10	10	6	10	7
初三（4）班	10	8	8	9	8
初三（8）班	9	10	9	6	9

　 （1）请问各班五项考评分的平均数、中位数和众数中哪个统计量不能反映三个班的考评结果的差异？并从中选择一个能反映差异的统计量将他们得分进行排序；

　 （2）根据你对表中五个项目的重要程度的认识，设定一个各项考评内容的占分比例（比例的各项须满足：①均为整数；②总和为10；③不全相同），按这个比例对各班的得分重新计算，比较出大小关系，并从中推荐一个得分最高的班级作为市级先进班集体的候选班.

24、（本题10分）为美化环境，计划在某小区内用30平方米的草皮铺设一个边长为10米的等腰三角形绿地，请你求出这块等腰三角形绿地另两边的长。

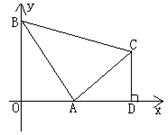
25.（本题10分）已知如图，直线y=-2x+2与x轴分别交于点A、B，以线段AB为直角边在第一象限内作等腰Rt△ABC，∠BAC=90°，过C作CD⊥x轴，垂足为D。（1）求点A、B的坐标和AD的长；

（2）求过B、A、D三点的抛物线的解析式。

26．（本小题12分）仔细观察下图，认真阅读对话：

根据对话的内容，试求出饼干和牛奶的标价各是多少元？

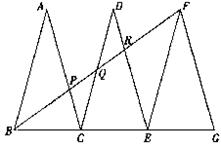
27．（本小题12分）如图，已知△ABC、△DCE、△FEG是三个全等的等腰三角形，底边BC、CE、EG在同一直线上，且AB=，BC=1.连结BF，分别交AC、DC、DE于点P、Q、R.

　 （1）求证：△BFG∽△FEG，并求出BF的长；

　 （2）观察图形，请你提出一个与点P相关的问题，并进行解答（根据提出问题的层次和解答过程评分）.

28、（本小题14分）

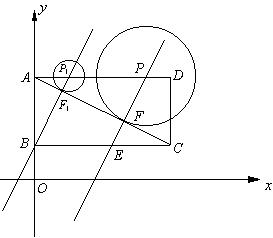
已知，如图，直角坐标系内的矩形ABCD，顶点A的坐标为（0，3），BC＝2AB，P为AD边上一动点（与点A、D不重合），以点P为圆心作⊙P与对角线AC相切于点F，过P、F作直线L，交BC边于点E ，当点P运动到点P₁位置时，直线L恰好经过点B，此时直线的解析式是y＝2x＋1

⑴求BC、AP₁的长；

⑵设AP＝m，梯形PECD的面积为S，求S与m之间的函数关系式，写出自变量m的取值范围；

⑶以点E为圆心作⊙E与x轴相切

①探究并猜想：⊙P和⊙E有哪几种位置关系，并求出AP相应的取值范围；

②当直线L把矩形ABCD分成两部分的面积之比值为3∶5时，则⊙P和⊙E的位置关系如何？并说明理由。