直线与圆 圆与圆
（一）直线与圆的位置关系知识点：（设
为圆心的距离，
为圆的半径）填下表：
| 直线与圆的位置关系 | 图形 |
| 公共点的个数 |
| 相交 | |||
| 相切 | |||
| 相离 |
练习：1、在△ABC中，∠C=90°，AC=3，AB=6，若以C为圆心，以为半径作圆，求
（1）当直线AB与⊙C相离时，的取值范围；（2）当直线AB与⊙C相切时，的取值范围；（3）当直线AB与⊙C相交时，的取值范围；
2、已知∠AOB=45°，在边OA上取点P，使OP=6厘米，以P为圆心，为半径作圆。（1）若⊙P与射线OB有两个交点，求⊙P的半径的取值范围；（2）若⊙P与射线OB有一个交点，求⊙P的半径的取值范围；
（二）切线的辅助线：一见到切线，连 和 ，得 。
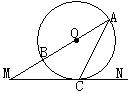
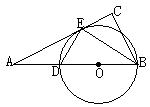
3．如图AB为⊙O的直径，MN切⊙O于C，交AB的延长线于M，∠CAN=68°，求∠M。
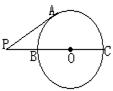
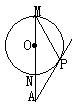
4．如图BC为直径，P为CB的延长线上一点，PA切⊙O于A，∠APC=30°，PA=
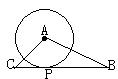
，求PB。5、如图MN为⊙O直径，AP是⊙O的切线，P为切点，A在MN的延长线上，若PA=PM，求∠PAM。6、如图，△ABC中，AB=4，AC=
，若以A为圆心，2为半径的圆与BC相切，求∠BAC的度数。7、如图AB为直径，直线CD切⊙O于P点，点A和点B到CD的距离为AD和BC，（1）求证：AB=AD+BC；（2）若PE⊥AB于E，求证：
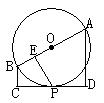
第3题 第4题 第5题 第6题 第7题
8．如图，两同心圆，大圆的弦AB切小圆于M，若环形的面积为
，求AB的长。
9．如图，AB切⊙O于B，BC是直径，DE是切线，CE⊥DE，CE=4，求AB的长。
（三）切线的证明方法的两种辅助线：（1）已知切点， ；（2）不知切点， 。
10．如图，以RT△ABC的直角边AC为直径作圆⊙O，交斜边AB于D，E是另一条直角边BC的中点，（1）求证：DE是⊙O的切线；（2）如果AD=4，BD=
，求DE的长。
11．如图，在△ABC中，∠C=90°，BE是∠ABC的平分线，DE⊥BE，⊙O是△BDE的外接圆，求证：（1）AC是⊙O的切线；（2）若AD=6，AE=
，求DE的长。
12．如图已知AB是半圆O的直径，AD、BC分别与半圆切于A、B两点，若∠COD=90°，求证：DC为⊙O的切线。
13．如图，在直角△ABC中，∠B=90°，∠A的平分线交BC于D，E为AB上一点，DE=DC，
以D为圆心，DB长为半径作⊙D，求证：（1）AC为⊙D的切线；（2）AB+EB=AC
14．如图，⊙O内接△ABC，弦AD平分∠BAC，过点D作直线EF∥BC，求证：EF是⊙O的切线。
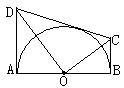
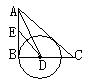
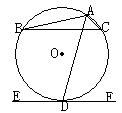
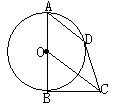
15．如图，AB是⊙O的直径，BC是⊙O的切线，弦AD∥OC，求证：（1）DC是⊙O的切线；（2）若⊙O的半径为10厘米，求AD OC的值。
（四）外心、内心：（1）填表：
| 定义 | 图形 | 性质 | |
| 内心 | |||
| 外心 |
（2）切线的重要结论：① ；② ；③ 。
16．△ABC中，∠A=120°，AB=AC=3，求△ABC的外接圆的半径。
17．若直角△ABC的斜边是AB，它的外接圆面积为144
，求AB。
18．△ABC三边为3，2，
，设其三条高线的交点为H，外心为O，求OH的长。
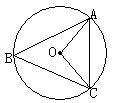
19、如图，⊙O是△ABC的外接圆，连接OA，OC，⊙O的半径为2，
，求弦AC。
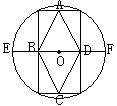
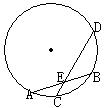
20．如图，顺次连结圆内接矩形各边的中点，得到菱形ABCD，若BD=10，DF=4，求菱形ABCD的边长。21．如图，已知⊙O的两条弦AB、CD相交于AB的中点，且AB=4，DE=CE+3，求CD的长。22、△ABC中，AB=AC=13，△ABC的面积为60，求△ABC内切圆的半径。
（五）圆与圆的位置关系：
| 位置 关系 | 图形 | 圆心距 半径的关系 | 交点个数 | 公切线 的条数 | 连心线的性质 |
| 外切 | |||||
| 内切 | |||||
| 外离 | |||||
| 内含 | |||||
| 相交 |