中等学校招生统一考试数学试题
本试题分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至2页,第Ⅱ卷3至8页.全卷共27题,满分130分.考试时间120分钟.
第I卷(选择题 共36分)
考生注意:
1.答第Ⅰ卷前,考生务必在答题卡上用钢笔或圆珠笔填写自己的姓名、考试号,用2B铅笔填涂考试号、考试科目,同时在第1页右下角填写座位号.
2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用塑胶橡皮擦干净后,再选涂其它答案,答案答在试卷上无效.
3.考试结束,监考人员将本试卷和答题卡一并收回.
一、选择题(下列各题给出的四个选项中,只有一个是正确的.每小题3分)
1.若![]() ,则下列各式中一定成立的是
,则下列各式中一定成立的是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
2.在推荐“美猴王”孙悟空为2008年北京奥运会吉祥物的活动中,我市共印制了2 000 000枚申吉专用邮资封.2 000 000用科学记数法可表示为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
3.与算式![]() 的运算结果相等的是
的运算结果相等的是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
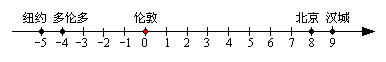 4.北京等5个城市的国际标准时间(单位:小时)可在数轴上表示如下:
4.北京等5个城市的国际标准时间(单位:小时)可在数轴上表示如下:
如果将两地国际标准时间的差简称为时差,那么
(A)汉城与纽约的时差为13小时 (B)汉城与多伦多的时差为13小时
(C)北京与纽约的时差为14小时 (D)北京与多伦多的时差为14小时
5.如果三角形的每条边都扩大为原来的5倍,那么三角形的每个角
(A)都扩大为原来的5倍 (B)都扩大为原来的10倍
(C)都扩大为原来的25倍 (D)都与原来相等
6.满足“两实数根之和等于3”的一个方程是
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
7.已知平面内两圆的半径分别为4和6,圆心距是2,则这两个圆的位置关系是
(A)内切 (B)相交 (C)外切 (D)外离
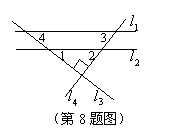 8.如图,直线
8.如图,直线![]() ∥
∥![]() ,
,![]() ⊥
⊥![]() .有三个命题:
.有三个命题:
①![]() ;②
;②![]() ;③
;③![]() .
.
下列说法中,正确的是
(A)只有①正确 (B)只有②正确
(C)①和③正确 (D)①②③都正确
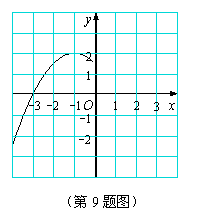 9.抛物线
9.抛物线![]() 的一部分如图所示,该
的一部分如图所示,该
抛物线在![]() 轴右侧部分与
轴右侧部分与![]() 轴交点的坐标是
轴交点的坐标是
(A)(![]() ,0)
(B)(1,0)
,0)
(B)(1,0)
(C)(2,0) (D)(3,0)
10.在ΔABC中,![]() ,D是边BC上的一点,
,D是边BC上的一点,
DE∥CA交AB于点E, DF∥BA交AC于点F.
要使四边形AEDF是菱形,只需添加条件
(A)AD![]() (B)
(B)![]()
(C)![]() (D)AD
(D)AD![]()
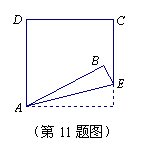 11.如图,将正方形ABCD的一角折叠,折痕为AE,
11.如图,将正方形ABCD的一角折叠,折痕为AE,
![]() 比
比![]() 大
大![]() .设
.设![]() 和
和![]() 的度数
的度数
分别为![]() ,
,![]() ,那么
,那么![]() ,
,![]() 所适合的一个方程组是
所适合的一个方程组是
(A)![]() (B)
(B)![]()
 (C)
(C)![]() (D)
(D)![]()
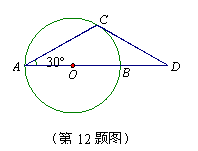
12.如图,⊙![]() 的直径
的直径![]() 与弦
与弦![]() 的夹角为
的夹角为![]() ,切线
,切线
![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,若⊙
,若⊙![]() 的半径为3,则
的半径为3,则
![]() 的长为
的长为
(A)6
(B)![]()
(C)3
(D)![]()
中等学校招生统一考试数学试题
第Ⅱ卷(非选择题 共94分)
| 总分 | 题号 | 二 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | |
| 得分 |
|
|
|
|
|
|
|
|
|
|
考生注意:
1.答第Ⅱ卷前,考生务必将自己的姓名、考试号、座位号填写在指定的位置.
2.考生答题时只能用蓝色或黑色钢笔、圆珠笔将试题答案书写在试卷规定位置上,写在草稿纸上无效.
| 得分 | 评卷人 | 复评人 |
二、填空题(每小题3分,共18分.请将答案直接填在题中横
线上)
13.计算:![]() =
.
=
.
14.如果![]() 的值为5,那么
的值为5,那么![]() 的值是
.
的值是
.
15.已知一个五边形的4个内角都是![]() ,则第5个内角的度数是
.
,则第5个内角的度数是
.
16.某公司2002,2004年的营业额分别为80万元、180万元,若2003,2004,2005这三年的年增长率都相同,则该公司2005年的营业额应为 万元.
 17.用一张半径为9cm、圆心角为
17.用一张半径为9cm、圆心角为![]() 的扇形纸片,做成一个圆锥形冰淇淋的侧面(不计接缝),那么这个圆锥形冰淇淋的底面半径是 cm.
的扇形纸片,做成一个圆锥形冰淇淋的侧面(不计接缝),那么这个圆锥形冰淇淋的底面半径是 cm.
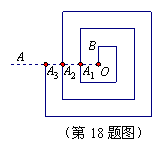
18.右图是一回形图,其回形通道的宽和![]() 的长均为1,
的长均为1,
回形线与射线![]() 交于
交于![]() ….若从
….若从![]() 点到
点到![]() 点
点
的回形线为第1圈(长为7),从![]() 点到
点到![]() 点的回形线
点的回形线
为第2圈,…,依此类推.则第10圈的长为 .
三、解答题 (共76分.解答应写出必要的文字说明、演算步骤
或证明过程)
| 得分 | 评卷人 | 复评人 |
19.(每小题满分6分,共12分)
(1)计算:![]() ; (2)化简:
; (2)化简:![]() .
.
| 得分 | 评卷人 | 复评人 |
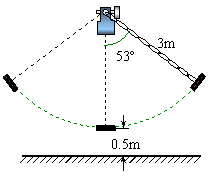
20.(本小题满分6分)
如图所示,秋千链子的长度为3m,静止时的秋千踏板(大小忽略不计)距地面0.5m.秋千向两边摆动时,若最大摆角(摆角指秋千链子与铅垂线的夹角)约为![]() ,则秋千踏板与地面的最大距离约为多少?(参考数据:
,则秋千踏板与地面的最大距离约为多少?(参考数据:![]() ≈0.8,
≈0.8,![]() ≈0.6)
≈0.6)
 | |||
| |||
| 得分 | 评卷人 | 复评人 |
21.(本小题满分6分)
 如图,在
如图,在![]() 中,
中,![]() ,
,![]() 是
是![]() 的中位线,点
的中位线,点![]() 在
在![]() 延长上,且
延长上,且![]() .求证:四边形
.求证:四边形![]() 是等腰梯形.
是等腰梯形.
| 得分 | 评卷人 | 复评人 |
22.(本小题满分6分)
今年“五一黄金周”期间,花果山风景区共接待游客约22.5万人.为了了解该景区的服务水平,有关部门从这些游客中随机抽取450人进行调查,请他们对景区的服务质量进行评分,评分结果的统计数据如下表:
| 档 次 | 第一档 | 第二档 | 第三档 | 第四档 | 第五档 |
| 分值a(分) | a≥90 | 80≤a<90 | 70≤a<80 | 60≤a<70 | a<60 |
| 人 数 | 73 | 147 | 122 | 86 | 22 |
根据表中提供的信息,回答下列问题:
(1)所有评分数据的中位数应在第几档内?
(2)若评分不低于70分为“满意”,试估计今年“五一黄金周”期间对花果山景区服务“满意”的游客人数.
| 得分 | 评卷人 | 复评人 |
23. (本小题满分8分)
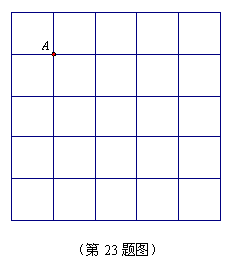 如图,在
如图,在![]() 的正方形网格中,每个小正
的正方形网格中,每个小正
方形的边长都为1.请在所给网格中按下列要求画
出图形.
(1)从点A出发的一条线段AB,使它的另一
个端点落在格点(即小正方形的顶点)上,
且长度为![]() ;
;
(2)以(1)中的AB为边的一个等腰三角形
ABC,使点C在格点上,且另两边的长
都是无理数;
(3)以(1)中的AB为边的两个凸多边形,使
它们都是中心对称图形且不全等,其顶点都
在格点上,各边长都是无理数.
| 得分 | 评卷人 | 复评人 |
24.(本小题满分8分)
光明农场现有某种植物10 000kg,打算全部用于生产高科技药品和保健食品.若生产高科技药品,1kg该植物可提炼出0.01kg的高科技药品,将产生污染物0.1kg;若生产保健食品,1kg该植物可制成0.2kg的保健食品,同时产生污染物0.04kg.已知每生产1kg高科技药品可获利润5 000元,每生产1kg保健食品可获利润100元.要使总利润不低于410 000元,所产生的污染物总量不超过880kg,求用于生产高科技药品的该植物重量的范围.
| 得分 | 评卷人 | 复评人 |
25.(本小题满分10分)
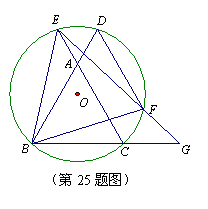 如图,
如图,![]() 是等边三角形,⊙O过点B,C,且与
是等边三角形,⊙O过点B,C,且与![]() 的延长线分别交于点D,E.弦
的延长线分别交于点D,E.弦![]() ∥
∥![]() ,
,![]() 的延长线交
的延长线交![]() 的延长线于点G.
的延长线于点G.
(1)求证:![]() 是等边三角形;
是等边三角形;
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
| 得分 | 评卷人 | 复评人 |
26.(本小题满分10分)
据某气象中心观察和预测:发生于![]() 地的沙尘暴一直向正南方向移动,其移动速度
地的沙尘暴一直向正南方向移动,其移动速度![]() (km/h)与时间
(km/h)与时间![]() (h)的函数图象如图所示.过线段
(h)的函数图象如图所示.过线段![]() 上一点
上一点![]() 作横轴的垂线
作横轴的垂线![]() ,梯形
,梯形![]() 在直线
在直线![]() 左侧部分的面积即为
左侧部分的面积即为![]() h内沙尘暴所经过的路程
h内沙尘暴所经过的路程![]() (km).
(km).
(1)当![]() 时,求
时,求![]() 的值;
的值;
(2)将s随![]() 变化的规律用数学关系式表示出来;
变化的规律用数学关系式表示出来;
(3)若![]() 城位于
城位于![]() 地正南方向,且距
地正南方向,且距![]() 地650km,试判断这场沙尘暴是否会侵袭到
地650km,试判断这场沙尘暴是否会侵袭到![]() 城.如果会,在沙尘暴发生后多长时间它将侵袭到
城.如果会,在沙尘暴发生后多长时间它将侵袭到![]() 城?如果不会,请说明理由.
城?如果不会,请说明理由.
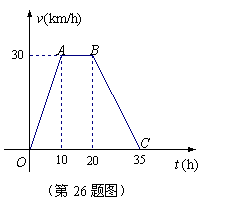 |
| 得分 | 评卷人 | 复评人 |
27.(本小题满分10分)
如图,将一块直角三角形纸板的直角顶点放在![]() 处,两直角边分别与
处,两直角边分别与![]() 轴平行,
轴平行,
纸板的另两个顶点![]() 恰好是直线
恰好是直线![]() 与双曲线
与双曲线![]() 的交点.
的交点.
(1)求![]() 和
和![]() 的值;
的值;
(2)设双曲线![]() 在
在![]() 之间的部分为
之间的部分为![]() ,让一把三角尺的直角顶点
,让一把三角尺的直角顶点![]() 在
在![]() 上
上
滑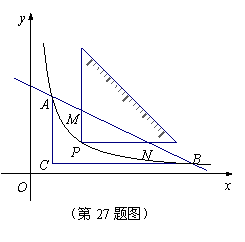 动,两直角边始终与坐标轴平行,且与线段
动,两直角边始终与坐标轴平行,且与线段![]() 交于
交于![]() 两点,请探究是否存在点
两点,请探究是否存在点![]() 使得
使得![]() ,写出你的探究过程和结论.
,写出你的探究过程和结论.