中等学校招生文化统一考试数学试题
欢迎你参加中考。祝你取得好成绩!请先阅读以下几点注意事项：
1．本卷分第Ⅰ卷(机器阅卷)和第Ⅱ卷(人工阅卷)两部分．共130分，考试时间120分钟．
2．做第Ⅰ卷时，请将每小题选出的答案用2B铅笔将答题卡上对应的题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其他答案．答案写在试题卷上无效．
3．做第Ⅱ卷时，请先将密封线内的项目填写清楚，然后，用蓝色、黑色钢笔、签字笔或圆珠笔直接在试卷上作答，写在试题卷外无效．
4．考试结束后，将第Ⅰ卷、第Ⅱ卷和答题卡一并交回．
第Ⅰ卷
一、选择题(下列各题的四个选项中，只有一个选项是符合题意的)
1．-
的相反数是
A．2 B． C．- D．-2
2．若等腰三角形底角为72°，则顶角为
A．108° B．72° C．54° D．36°
3．方程x2+4x=2的正根为
A．2-
B．2+ C．-2- D．-2+
4．下面图示的四个物体中，正视图如右图的有
A．1个 B．2个 C．3个 D．4个
5．下列调查方式，合适的是
A．要了解一批灯泡的使用寿命，采用普查方式
B．要了解淮安电视台“有事报道”栏目的收视率，采用普查方式
C．要保证“神舟六号”载人飞船成功发射，对重要零部件的检查采用抽查方式
D．要了解外地游客对“淮扬菜美食文化节”的满意度，采用抽查方式
6．一圆锥的侧面展开后是扇形，该扇形的圆心角为120°，半径为6cm，则此圆锥的表面积为
A．4
cm2 B．12cm2 C．16cm2 D．28cm2
7．正比例函数与反比例函数图象都经过点(1，4)，在第一象限内正比例函数图象在反比例函数图象上方的自变量x的取值范围是
A．x>1 B．O<x<1 C．x>4 D．0<x<4
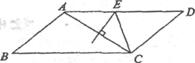
8．如图，平行四边形ABCD中，AB=3，BC=5，AC的垂直平分线交AD于E，则△CDE的周
长是
A．6 B．8 C．9 D．10
9．巳知某种型号的纸100张厚度约为lcm，那么这种型号的纸13亿张厚度约为
A．1.3×107km B．1.3×103km C．1.3×102km D．1.3×10km
lO．如图，正方形ABCD的边长为2，点E在AB边上．四边形EFGB也为正方形，设△AFC
的面积为S，则
A．S=2 B．S=2.4 C．S=4 D．S与BE长度有关
第Ⅱ卷
二、填空题
11．计算：a2·(ab)3=________．
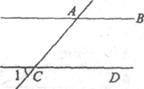
12．如图，已知AB∥CD，若∠1=50°，则∠BAC=________度．
13.已知实数x满足4x2-4x+l=O，则代数式2x+
的值为________．
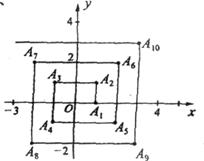
14．如图，已知Al(1，0)、A2(1，1)、A3(-1，1)、A4(-1，-1)、 A5(2，-1)、…。则点A2007，的坐标为________．
15．计算：
16．已知
，求
的值．
17．已知：线段m、n
(1)用尺规作出一个等腰三角形，使它的底等于m,腰等于n(保留作图痕迹，不写作法、不证明)；
(2)用至少4块所作三角形，拼成一个轴对称多边形(画出示意图即可)．
18．在“不闯红灯，珍惜生命”活动中，文明中学的关欣和李好两位同学某天来到城区中心的十字路口，观察、统计上午7：00～12：00中闯红灯的人次．制作了如下的两个数据统计图．
(1)求图(一)提供的五个数据(各时段闯红灯人次)的众数和平均数．
(2)估计一个月(按30天计算)上午7：00～12：00在该十字路口闯红灯的未成年人约
有________人次．
(3)请你根据统计图提供的信息向交通管理部门提出一条合理化建议．
19．小明放学回家后，问爸爸妈妈小牛队与太阳队篮球比赛的结果．爸爸说：“本场比赛太阳队的纳什比小牛队的特里多得了12分．”妈妈说：“特里得分的两倍与纳什得分的差大于10；纳什得分的两倍比特里得分的三倍还多．”爸爸又说：“如果特里得分超过20分，则小牛队赢；否则太阳队赢．”请你帮小明分析一下．究竟是哪个队赢了，本场比赛特里、纳什各得了多少分?
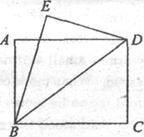
20．如图，AB=CD=ED，AD=EB，BE⊥DE，垂足为E．
(1)求证：△ABD≌△EDB
(2)只需添加一个条件，即________，可使四边形ABCD为矩形.请加以证明.
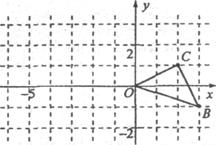
2l.如图,已知O是坐标原点，B、C两点的坐标分别为(3，-1)、(2,1)．
(1)以0点为位似中心在y轴的左侧将△OBC放大到两倍(即新图与原图的相似比为2)，画出图形；
(2)分别写出B、C两点的对应点B′、C′的坐标；
(3)如果△OBC内部一点M的坐标为(X，y),写出M的对应点M′的坐标．
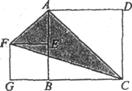
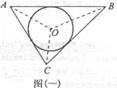
22．阅读材料：如图(一)，△ABC的周长为
，内切圆O的半径为r,连结OA、OB、OC，△ABC
被划分为三个小三角形，用S△ABC表示△ABC的面积
∵ S△ABC=S△OAB+S△OBC+S△OCA
又∵S△OAB=
，S△OBC=
，S△OCA =
∴S△ABC=++=
(可作为三角形内切圆半径公式)
(1)理解与应用：利用公式计算边长分为5、12、13的三角形内切圆半径；
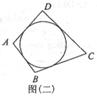
(2)类比与推理：若四边形ABCD存在内切圆(与各边都相切的圆，如图(二))且面积为
S，各边长分别为a、b、c、d，试推导四边形的内切圆半径公式；
(3)拓展与延伸：若一个n边形(n为不小于3的整数)存在内切圆，且面积为S，各边长分别为a1、a2、a3、…、an，合理猜想其内切圆半径公式(不需说明理由)．
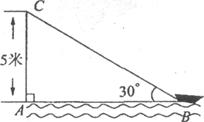
23. 如图，在离水面高度为5米的岸上有人用绳子拉船靠岸，开始时绳子与水面的夹角为30°，此人以每秒0.5米收绳．问：8秒后船向岸边移动了多少米?(结果精确到O.1米)
24.王强与李刚两位同学在学习“概率”时．做抛骰子(均匀正方体形状)实验，他们共抛了54次，出现向上点数的次数如下表：
| 向上点数 | 1 | 2 | 3 | 4 | 5 | 6 |
| 出现次数 | 6 | 9 | 5 | 8 | 16 | 10 |
(1)请计算出现向上点数为3的频率及出现向上点数为5的频率．
(2)王强说：“根据实验，一次试验中出现向上点数为5的概率最大．”
李刚说：“如果抛540次，那么出现向上点数为6的次数正好是100次．”
请判断王强和李刚说法的对错．
(3)如果王强与李刚各抛一枚骰子．求出现向上点数之和为3的倍数的概率．
25． 东方专卖店专销某种品牌的计算器，进价l2元／只，售价20元／只．为了促销,专卖店决定凡是买10只以上的，每多买一只，售价就降低O.10元(例如．某人买20只计算器，于是每只降价O.10×(20-10)=1元,就可以按19元／只的价格购买)，但是最低价为16元／只．
(1)求顾客一次至少买多少只，才能以最低价购买?
(2)写出当一次购买x只时(x>10)，利润y(元)与购买量x(只)之间的函数关系式；
(3)有一天，一位顾客买了46只，另一位顾客买了50只，专实店发现卖了50只反而比卖46只赚的钱少，为了使每次卖的多赚钱也多,在其他促销条件不变的情况下,最低价16元／只至少要提高到多少?为什么?
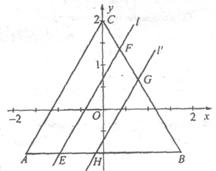
26．已知一次函数y=
+m(O<m≤1)的图象为直线，直线绕原点O旋转180°后得直线
，△ABC三个顶点的坐标分别为A(-，-1)、B(，-1)、C(O，2)．
(1)直线AC的解析式为________，直线的解析式为________ (可以含m)；
(2)如图，、分别与△ABC的两边交于E、F、G、H，当m在其范围内变化时，判断四边形EFGH中有哪些量不随m的变化而变化?并简要说明理由；
(3)将(2)中四边形EFGH的面积记为S，试求m与S的关系式，并求S的变化范围；
(4)若m=1，当△ABC分别沿直线y=x与y=x平移时，判断△ABC介于直线，之间部分的面积是否改变?若不变请指出来．若改变请写出面积变化的范围．(不必说明理由)
