中考数学冲刺模拟测试题(五)
一,填空题(每小题3分,共计30分) 姓名: 总分:
1,2004年我国的GDP(国民生产总值)已达到13.65亿元,用科学记数法表示这个数并保留3个有效数字,那么我国2004年的GDP是 元。
| B |
![]()
![]()
![]()
![]() 2,函数
2,函数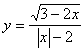 的自变量x的取值范围是
。
的自变量x的取值范围是
。
![]() 3,如图,一束光线AB和CD两个镜面之间反射,图中箭头所示为 A
3,如图,一束光线AB和CD两个镜面之间反射,图中箭头所示为 A
| C |
| D |
| α |
|
|
光线方向,测得∠α=65°,∠β=55°,那么∠γ= 。
![]()
![]() 4,如图,△ABC中,AB>AC,点D在AB边上,要使△ACD∽△ABC,
4,如图,△ABC中,AB>AC,点D在AB边上,要使△ACD∽△ABC,
![]() 那么应当补充的一个条件可以是
。
(第3题图)
那么应当补充的一个条件可以是
。
(第3题图)
| y |
| A |
| D |
| F |
 A
A
 |

|
|
| x |
| B |
| A |
|
|
| (1,0) |
| O |
| O |
| B C |
| 第4题图 |
| B |
| C |
| E |
| 第7题图 |
第6题图
5,设![]() 、
、![]() 是方程
是方程![]() +3x-2=0的两实数根,那么
+3x-2=0的两实数根,那么![]() =
。
=
。
| A |
6,如图,抛物线y=ax2+bx+c(a≠0)交x轴于A、B,那么抛物线的顶点的横坐标是 。
7,如图,平行四边形ABCD中,AC与BD相交于点O,过点O的线段交BC于E,交AD于F,若平行四边形ABCD的周长是18㎝,OE=2㎝,那么四边形ABEF的周长是 。
| 职务 | 经理 | 业务组长 | 业务员 | 辅助人员 |
| 人数 | 1 | 2 | 8 | 2 |
| 月工资 | 6000元 | 3000元 | 1500元 | 1000元 |
8,某业务公司工作人员的月工资统计如表,
这个公司工作人员月工资的平均数是 ;
中位数是 ;众数是 。
9,关于x的二次函数y=(k-1)x2+2kx+k+3的图象与x轴有两个交点,那么k的取值范围是 。
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 10,如下图,一张长方形桌子四周可坐10人,把桌子拼在一起,那么n张桌子(n是正整数)周围可坐的人数是
。
10,如下图,一张长方形桌子四周可坐10人,把桌子拼在一起,那么n张桌子(n是正整数)周围可坐的人数是
。
![]()
![]()
![]()
![]()
![]()
![]() 二,选择题(每题中只有一个正确
二,选择题(每题中只有一个正确
![]()
![]()
![]()
![]()
![]()
![]() 答案,每小题3分共计24分)
答案,每小题3分共计24分)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 11,下列各式的运算,正确的是( )
11,下列各式的运算,正确的是( )
A,![]() 第10题图
第10题图
B,![]() C,
C,![]() D,
D,![]()
12,多项式9a2+1-b2-6a因式分解的结果是( )A,(3a+b+1)(3a+b-1)
B,(3a+b-1)(3a-b-1) C,(3a-b+1)(3a-b-1) D,(3a+b+1)(3a-b-1)
13,在Rt△ABC中,∠C=90°,BC=![]() AC,那么∠A的度数或范围是( )
AC,那么∠A的度数或范围是( )
A,45° B,30° C,大于30° D,小于30°
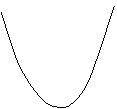
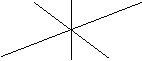
14,同一直角坐标系中,函数y=kx+k与![]() 的图象大致是( )
的图象大致是( )

![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]() y
y
y
y
y
y
y
y
 | |||
![]()
![]()
![]()
![]()
![]()
![]()
![]() O
x
O
x
O
x
O x
O
x
O
x
O
x
O x
A B C D
15,如图,△ABC中,∠A=90°,AB=8,AC=6,以点A为圆心作⊙A,当⊙A与BC边相交时,⊙A的半径R的取值范围是( ) A,R>5 B,R>4.8 C,5<R≤8 D,4.8<R≤8
16,在△ABC中,∠C=90°,下列关系式中,正确的个数是( )①sinA=cosB;②sin2B+cos2B=1;③tanA>sinA;④sinB+cosB>1。 A,4个 B,3个 C,2个 D,1个
17,已知⊙O的直径是2,⊙O的弦AB=1,弦AC=![]() ,那么∠BAC的度数为( )
,那么∠BAC的度数为( )
|
|
 A,30° B,15°或105° C,30°或120° D,60°
A,30° B,15°或105° C,30°或120° D,60°
| D |
| C |
![]()
![]()
![]() 18,如图,圆柱体的高是12㎝,底面半径是
18,如图,圆柱体的高是12㎝,底面半径是![]() ㎝,矩形ABCD是圆柱
㎝,矩形ABCD是圆柱
| E |
的纵截面;一只蚂蚁在A点处,食物在CB的中点E处,那么蚂蚁从
![]() 点A到点E的最短路程是(
)
点A到点E的最短路程是(
)
| B |
| O2 |
![]()
![]()
![]() A,10㎝ B,20㎝ C,
A,10㎝ B,20㎝ C,![]() ㎝
D,
㎝
D,![]() ㎝
㎝
三,解答题(共8个小题,共66分)
![]()
 19,(6分)计算:
19,(6分)计算:![]() A
A
B C
第15题图
20,(8分)解方程:![]()
![]()
![]() 21,(8分)如图,坐标平面内,A、B两点表示我省某地新建成的两个经济作物示范中心,y轴是一条公路干线;现在要在公路干线上确定一点P,从P点分别向A、B两个示范中心修建道路PA、PB,要使两条路的长度之和为最小,如何确定点P?两条道路的长度之和最小是多少?(做出图形,求出P点坐标,计算此时的AP+PB之值;
y
A(4,9)
21,(8分)如图,坐标平面内,A、B两点表示我省某地新建成的两个经济作物示范中心,y轴是一条公路干线;现在要在公路干线上确定一点P,从P点分别向A、B两个示范中心修建道路PA、PB,要使两条路的长度之和为最小,如何确定点P?两条道路的长度之和最小是多少?(做出图形,求出P点坐标,计算此时的AP+PB之值;
y
A(4,9)
坐标系中每一格表示1千米)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() O
B
x
O
B
x
(8,0)
22,(8分)为了解某区的初中数学考试成绩情况,从某校随机抽取一部分同学的数学成绩,进行分组统计,得到下面的频率分布表(满分为100分,成绩是整数)
| 组别 | 分组 | 频数 | 频率 |
| 1 | 49.5~59.5 | 3 | 0.06 |
| 2 | 59.5~69.5 | 5 | 0.10 |
| 3 | 69.5~79.5 | b | c |
| 4 | 79.5~89.5 | 18 | 0.36 |
| 5 | 89.5~100 | 0.26 | |
| 合计 | d | a |
|
|
|
|
49.5 59.5 69.5 79.5 89.5 100 成绩(分) |
(1)在这个问题中,什么是总体?求频率之和a,频数之和d的值;
(2)第3组中的频数b、频率c各是多少?
(3)根据这个样本,请你估计全区数学考试的及格率(60分为及格)和优秀率(90分及以上)各是多少?
(4)绘制频率分布直方图。
 23,(8分)要测量旗杆AB的高度,旗杆AB在阳光下的影子落在地面BC上及斜坡CD上(如图),测量得到斜坡坡角α=60°,BC=14米,CD=4米;在同一时刻,1米高的测杆的影子的长是2米;求旗杆的高度(结果保留根号)。
A
23,(8分)要测量旗杆AB的高度,旗杆AB在阳光下的影子落在地面BC上及斜坡CD上(如图),测量得到斜坡坡角α=60°,BC=14米,CD=4米;在同一时刻,1米高的测杆的影子的长是2米;求旗杆的高度(结果保留根号)。
A
 D
D
| α |
| E |
B C
24,(9分)AB是⊙O的直径,延长AB到点C,使BC=AB,过点C作⊙O的一条切线,切点为D,连接DA、DB,直径AB=6㎝;按题意画出图形(不写作法),求:
(1)切线CD的长;
(2)DA:DB的值;
(3)DA、DB的长;
(4)S△ACD(结果可保留根号)。
25,(9分)某工厂生产一种产品,每件产品的出厂价格是1万元,生产这种产品的成本费用是0.55万元,同时在生产过程中平均每生产1件产品产生1吨废渣,需要对废渣进行处理,避免污染环境;现有两种方案可供选择:方案一,由工厂建一套处理设备,每吨废渣的处理费为0.05万元,同时每月的设备维修及损耗费为18万元,也要计入支出费用;方案二,工厂把废渣送到废渣处理厂统一处理,每吨废渣的处理费是0.1万元,另外每吨废渣运输费为0.01万元;
(1)设工厂每月生产x件产品,每月的利润为y万元,求在方案一、方案二中,y与x的函数关系式;
| x |
(2)如何根据每月的生产量选择合理方案,既达到环保要求,又较合算?
26,(10分)如图,在平面直角坐标系中,点A坐标为(-2,0),⊙A的半径是4,⊙A交x轴于E、F两点,交y轴于C、D两点,过点C作⊙A的切线交x轴于点B;
(1)求直线BC的函数解析式;
![]() y
y
 |
C |

![]()
| B |
|
|
| A |
| O |
| E |
| D |
(2)若一条抛物线经过E、F两点,顶点在直线BC上,求抛物线的解析式;
(3)以点A、E、C为其中的三个顶点,作平行四边形AECP,那么点P是否在⊙A上?是否在上题所求的抛物线上?为什么?