九年级数学下学期月考试卷
制卷:李军霞 时量:120分钟 满分:150分
一、填空题(每题4分,共48分)
1、若将![]() 配方成
配方成![]() 的形式,则
的形式,则![]() ;
;
2、二次函数![]() 的图象上有两点
的图象上有两点![]() 和
和![]() ,则此抛物线的对称轴是 ;
,则此抛物线的对称轴是 ;
3、已知![]() 与
与![]() 成反比例,且
成反比例,且![]() 时
时![]() ,则当
,则当![]() 时,
时,![]() ;
;
4、抛物线![]() 过第二、三、四象限,则
过第二、三、四象限,则![]() 0,
0,![]() 0 ;
0 ;
5、R![]() ABC中,∠C=90°,AB=15
ABC中,∠C=90°,AB=15![]() ,BC=10
,BC=10![]() ,以A为圆心,12
,以A为圆心,12![]() 为半径作圆,则C与⊙A的位置关系是
;
为半径作圆,则C与⊙A的位置关系是
;
6、平面直角坐标系中,⊙P的圆心P的坐标为(8,0),半径为6,那么直线![]() 与⊙P的位置关系为 ;
与⊙P的位置关系为 ;
7、直角三角形三边长分别为6,8,10,那么这个三角形的外接圆半径为 ;内切圆半径为 ;
8、已知⊙![]() 与⊙
与⊙![]() 内切于点P,⊙
内切于点P,⊙![]() 的半径为5,且
的半径为5,且![]() =3,则⊙
=3,则⊙![]() 的半径为
;
的半径为
;
9、时钟上的分针经过25分钟后扫过的钟面面积为![]() ,则分针长为 ;
,则分针长为 ;
 10、已知扇形的弧长是
10、已知扇形的弧长是![]()
![]() ,半径为12
,半径为12![]() ,用它做成一个圆锥的侧面,则此圆锥的高线长为
;
,用它做成一个圆锥的侧面,则此圆锥的高线长为
;
11、如图,AB是半圆O的直径,C为半圆上一点,E是
弧AC的中点,OE交弦AC于点D,若AC=8![]() ,
,
DE=2![]() ,则OD的长为
;
,则OD的长为
;
12、李大伯为了与客户签订购销合同,对自己鱼塘中的鱼的总质量进行估计,第一次捞出100条,称得总质量为184千克,并将每条鱼作好记号放入水中,当它们完全混合于鱼群后,又捞出200条,称得质量为416千克,且带有记号的鱼有20条,李大伯的鱼塘中估计有鱼 条,共 千克。
二、选择题(每题4分,共40分)
13、⊙O的半径为5,直线上一点P到⊙O点的距离为5,则直线与⊙O的位置关系是( )
(A)相交 (B)相离 (C)相切 (D)不相离
14、已知AB、CD是⊙O的两条直径,则四边形ABCD一定是( )
(A)等腰梯形 (B)矩形 (C)正方形 (D)菱形
15、把半圆的直径分为![]() 份,以每一份为直径画
份,以每一份为直径画![]() 个小半圆,则这
个小半圆,则这![]() 个小半圆的弧长之和S与已知半圆的弧长C的关系是( )
个小半圆的弧长之和S与已知半圆的弧长C的关系是( )
(A)C=S (B)![]() (C)
(C)![]() (D)不确定
(D)不确定
16、抛物线![]() 与
与![]() 轴的交点都在原点右侧,则点M
轴的交点都在原点右侧,则点M![]() 在第( )象限。
在第( )象限。
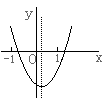 (A)一
(B)二
(C)三
(D)四
(A)一
(B)二
(C)三
(D)四
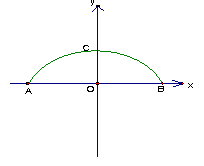
17、二次函数![]() 的图象如图所示,则
的图象如图所示,则
![]()
![]() ,
,![]() ,
,![]() ,
,![]() 这四个式子中,
这四个式子中,
![]() 值为正数的有( )
值为正数的有( )
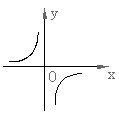 (A)4个
(B)3个 (C)2个 (D)1个
(A)4个
(B)3个 (C)2个 (D)1个
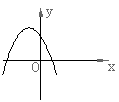
18、已知反比例函数![]() 的图象如右图所示,则二次函数
的图象如右图所示,则二次函数![]()
的图象大致为( )
| ||||||||
|
| |||||||
| ||||||||
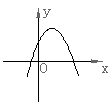
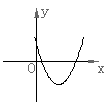
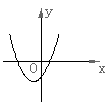
19、已知反比例函数![]() 的图象上有两点
的图象上有两点![]() ,当
,当![]() 时有
时有![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)以上都不对
(D)以上都不对
20、下列函数关系中,可以看作二次函数模型的是( )
(A)在一定的距离内汽车的行驶速度与时间的关系;
(B)我国人口年自然增长率为1%,这样我国人口总数随年份的变化关系;
(C)竖直向上发射的信号弹,从发射到落回地面,信号弹的高度与时间的关系;
(D)圆的周长与圆的半径之间的关系;
21、下列关系三角形的叙述正确的是( )
(A)三角形的外心是三角形三条角平分线的交点;
(B)三角形的内心是三角形三边中垂线的交点;
(C)正三角形的外接圆半径是内切圆半径的两倍
 (D)三角形的外心一定在三角形外
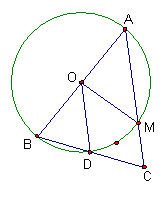
(D)三角形的外心一定在三角形外
22、![]() ABC中,AB=AC,以AB为直径的⊙O交BC于
ABC中,AB=AC,以AB为直径的⊙O交BC于
D交AC于M,则有:①![]() ②弧
②弧![]()
![]() ③
③![]() ④
④![]() ;这四个结论中正
;这四个结论中正
确的个数为( )
(A)1个 (B)2个 (C)3个 (D)4个
初 三 数 学 月 考 试 题 答 题 卷
一、填空题(每题4分,共48分)
1、 ; 2、 ; 3、 ;
4、 , ; 5、 ; 6、 ;
7、 , ; 8、 ; 9、 ;
10、 ; 11、 ; 12、 ; ;
二、选择题(每题4分,共40分)
| 题号 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 答案 |
三、解答题
23、已知抛物线![]() 与
与![]() 轴交于点A,与
轴交于点A,与![]() 轴的正半轴交于B(1,0)、C(3,0)两点,求
轴的正半轴交于B(1,0)、C(3,0)两点,求![]() 的值及三角形ABC的面积。(10分)
的值及三角形ABC的面积。(10分)
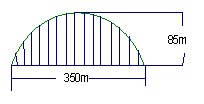
24、如图,一拱形桥的拱形图形为抛物线的一部分,在正常情况下,位于水面上的桥拱跨度为350米,拱高为85米。
(1)在所给的直角坐标系中,假设抛物线的表达式为![]() ,请根据上述数据求出
,请根据上述数据求出![]() 的值。
的值。
(2)七月份汛期将要来临,当江水水位上涨后,位于水面上的桥拱跨度将会减小,当水位上涨4米时,位于水面上的桥拱跨度为多少(结果保留整数)(10分)
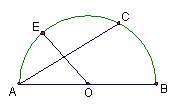
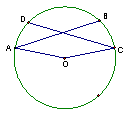
25、如图,AB、CD是⊙O的弦,∠A=∠C,求证:AB=CD(8分)
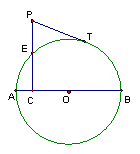
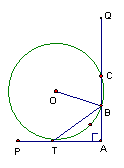
26、如图,PAQ是直角,半径为5的O与AP相切于点T,与AQ相交于点B,C。
(1)BT是否平分OBA?证明你的结论。
(2)若已知AT=4,试求AB的长。
27、如图,1---4,M、N分别是⊙O的内接正三角形ABC,正方形ABCD,正五边形ABCDE,正![]() 边形ABCDEF……的边AB、BC上的点,且BM=CN,连结OM,ON
边形ABCDEF……的边AB、BC上的点,且BM=CN,连结OM,ON
(1)图1中∠MON的度数为 ,图2中∠MON= ,图3中∠MON
=
 (2)试探究∠MON的度数与正
(2)试探究∠MON的度数与正![]() 边形边数
边形边数![]() 的关系(直接写出答案)
的关系(直接写出答案)
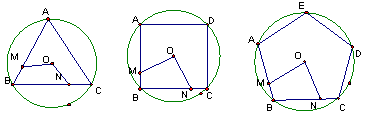
图1 图2 图3 图4
28、如图,已知AB是定圆的直径,O是圆心,点C在⊙O的半径OA上运动,PC⊥AB交⊙O于E,交AB于C,PC=5,PT是⊙O的切线(T为切点)
(1)当CE正好是⊙O的半径时,PT=3,求⊙O的半径;
(2)当C点与A点重合时,求CT的长。
(3)设PT2=![]() ,AC=
,AC=![]() ,写出
,写出![]() 关于
关于![]() 的函数关系式并确定
的函数关系式并确定![]() 的取值范围。
的取值范围。