九年级下学期期中数学试卷
姓名 班级 得分 -
一．
填空（3分
8=24分）
1．
已知抛物线y=
与x轴的交点的横坐标为1，则a+c=
2．
不论x取什么实数，二次函数y=
的函数值总是正数，
则m的取值范围是
3．
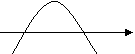
如图，所示的桥拱是抛物线形，上面有一点P（2，-1），
当水位线在AB位置时， A B
水面宽12m，则这时水面离桥顶的高度为
4． 二次函数的顶点为M（1，5），在x轴上截的线段长为8，那么它的解析式为
5．
如图，抛物线y=与x轴交于A，B，与y轴交于C点，y
若OA=OC，则a,b,c之间的关系为
。
C
6．关于一个二次函数的图象，三位学生分别说出了它的一些特点：
甲：对称轴是直线x=4， A O B x
乙：与x轴两个交点的横坐标都是整数；
丙：与y轴的交点的纵坐标也是整数，且以这三个交点为顶点的三角形的面积为3，
请你写出满足上述全部特征的一个二次函数解析式：
7．
用反证法证明命题“三角形至少有两个锐角”时，
A
N D
第一步假设 。
8． 如图，正方形ABCD的边长为1，三角形ABC是正三角形，
则此正三角形的边长为 。
二．选择（3分10=30分） M
1．当ab<0，且
>4ac时，抛物线的顶点一定位于（ ） B C
A．第一象限 B。第四象限 C。第一象限或第四象限 D。无法确定
2．若二次函数
中，当x取
时，函数值相等，当x取
时，函数值为（ ）
A．a+c B。a-c C。-c D。c
3．已知二次函数y=
，当x<-2时，y随x的增大而减小，当x>-2时，y随x的增大而增大。则当x=1时，函数y的值是（ ）
A．-7 B。1 C。17 D。25
4．抛物线y=的图象如图所示，则下列式子能成立的是（ ）
A．abc<0 B。a+b+1<0 C。b<a+c D。2c<3b
5．改革开放以来，某镇通过多种途径发展地方经济，1997年该镇国民生产总值为2亿元，根据测算，该镇年国民生产总值为5亿元时，可达到小康水平。设以2003年为第一年，该镇第x年的国民生产总值为y元，y与x之间的关系是y=
（x≥0）。该镇哪一年的国民生产总值可在1997年的基础上翻两番（即达到1997年的年国民生产总值的4倍）
A．2003 B。2004 C。2005 D。2006
6．在菱形ABCD中，若
，则BD：AC为（ ）
A．
：2 B。：3 C。1：2 D。：1
7．已知等腰梯形ABCD中，BC∥AD，AD<BC，EF为中位线，EF=28cm，周长为104cm，AD比AB少20cm，则AD：AB：BC=（ ）
A．8：12：5 B。2：3：5 C。8：12：20 D。9：12：19
8．已知矩形对角线长为10cm，那么顺次连结矩形四边中点所得的四边形的周长为（ ）
A．40cm B。10cm C。5cm D。20cm
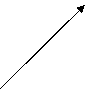9．如图所示，光线L射到平面镜I上，然后在平面镜I，II之间来回反射，已知
则
（ ）
A．50 B55 C。60 D。65 
10．已知三角形ABC的周长为1，连结各边中点
构成第二个三角形，再连结第二个三角形再连结 
各边中点构成第三个三角形，依次类推第2004个
三角形的周长为（ ）
A 。
B。
C。
D。
三，解答题（6+6+6+8+8+12=46分）
1．
已知抛物线
（1） 试说明，无论m为何值，抛物线与x轴总有两个交点。
（2） 求m为何值时，抛物线与x轴的两个交点之间的距离为3。
2． 某商场经销某种商品，进价每件20元，经市场调研发现，按40元/件的售价出售，每天能卖60件，且售价每提高1元，每天少卖10件，问：售价定为多少元时，能保证每天利润最大？
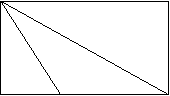3．折叠矩形纸片ABCD，先折出折痕（对角线BD），再折叠使AD边与对角线BD重合，得折痕DG，如图所示，若AB=2，BC=1，求AG。 D
C
A G B
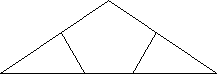
4．如图，
中，AB=AC，
=120
，D，F分别为AB，AC的中点，
，E，G在BC上，BC=15cm，求线段EG的长。
 |
A
D F
B E G C
5． 已知：四边形ABCD中，M，N分别是AB，CD的中点，根据题意画图，试判断MN与
（AD+BC）的大小关系，并证明你的结论。
6． 已知二次函数
的图象与x轴从左到右的两个交点依次为A，B，与y轴的交点为C。
（1） 求过B，C两点的一次函数的解析式。
（2） 如果P（x，y）是线段BC上一动点，O为坐标原点，试求
的面积S与x之间的函数关系，并求出自变量x的取值范围。
（3） 是否存在这样的点P，使得OP=OA？若存在，求出点P的坐标，若不存在，请说明理由。