九年级招生数学试卷

九年级招生数学试卷

　　　　　　　　　（本卷考试时间80分钟，满分120分）

一、填空题（把答案填在题中横线上，每小题7分，共70分）

1、已知a、b满足a²－2a－1＝0，b²－2b－1＝0，且a≠b，则＋＋1＝　　　　　　.

2、△ABC的周长是24，M是AB的中点，MC＝MA＝5，则△ABC的面积是　　　　　.

3、要使关于x的方程－＝的解为负数，则m的取值范围是　　　　.

4、已知：(b－c)²＝(a－b)(c－a)，且a≠0，则＝　　　　.

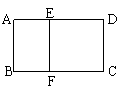
5、如图，E、F分别在AD、BC上，EFCD是正方形，且矩形

ABCD∽矩形AEFB，则AB∶BC的值是　　　　　.

	第5题

6、设x、y、z满足关系式x－1＝＝，则x²＋y²＋z²的最小值为　　　　　　.

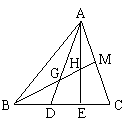
7、如图，在△ABC中，D、E是BC的三等分点，M是AC的中点，

BM交AD、AE于G、H则BG∶GH∶HM＝　　　　　　.

	第7题

8、如图3×3的正方形的每一条方格内的字母都代表某个数，已

a	b	c
d	e	F
g	h	i

知其每行、每列以及两条对角线上三角形个数之和都相等，若

a＝4，d＝19，i＝22，那么b＝　　　，h＝　　　.　　　　　　　　

	第8题

9、在矩形ABCD中，AB＝6cm，BC＝8cm，若将矩形折叠，使B

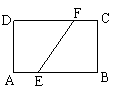点与D点重合，如图所示，则折痕EF的长为　　　　　　.

	第9题

10、如图，已知ABCD是一个半径为R的圆内接四边形，AB＝12，

CD＝6，分别延长AB和DC，它们相交于点P，且BP＝8，

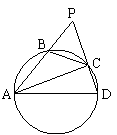∠APD＝60⁰，则R＝　　　　　　.

	第10题

二、解答题（本大题共4小题，共50分，解答应写出文字说明、证明过程或演算步骤）

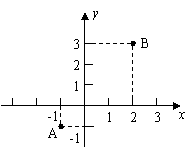11、如图，在直角坐标系内有两个点A（－1，－1），B（2,3），若M为x轴上一点，且使MB－MA最大，求M点的坐标，并说明理由.（10分）

	第11题

12、分别求所有的实数k，使得关于x的方程kx²＋(kx＋1)x＋(k－1)＝0

　　（1）有实根　　　（2）都是整数根　　　（12分）

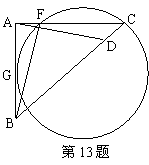
13、如图，设△ABC是直角三角形，点D在斜边BC上，BD＝4DC，已知圆过点C且与AC相交于F，与AB相切于AB的中点G.　求证：AD⊥BF.　（14分）

月　份	用水量	水　费
一	9 m3	9元
二	15 m3	19元
三	22 m3	33元

14、我国是水资源比较贫乏的国家之一，各地采用价格调控等手段来达到节约用水的目的，某市用水收费方法是：水费＝基本费＋超额费＋损耗。若每月用水量不超过最低限量a m³时，只付基本费8元和每户每月的定额损耗费c元；若用水量超过a m³时，除了付同上的基本费用和损耗费外，超过部分每立方米付b元超额费。已知每户的定额损耗费c不超过5元。

　　　　该市一家庭今年一月份、二月份、

三月份的用水量和支出费用如表所示：

　　　　根据右表提供的数据，求a、b、c.

（14分）