数学初中毕业学业考试试卷
| 大题 | 一 | 二 | 三 | 总分 | 合分人 | 复分人 | ||||||||
| 小题 | 1-8 | 9-16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | |||
| 得分 | ||||||||||||||
考生注意:本学科试卷共三道大题25小题,满分120分,考试时量120分钟.
一、选择题(把下列各题中唯一正确答案的序号填在题后的括号内.本题8个小题,每小题3分,满分24分)
1.![]() 的倒数是( )
的倒数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.若一个多边形的每个外角都等于![]() ,则它的边数是( )
,则它的边数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.下列运算不正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
4.有4条线段,分别为![]() ,
,![]() ,
,![]() ,
,![]() ,从中任取
,从中任取![]() 条,能构成直角三角形的概率是( )
条,能构成直角三角形的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.已知正三角形外接圆半径为![]() ,这个正三角形的边长是( )
,这个正三角形的边长是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.分解因式:![]() 的结果是( )
的结果是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
7.如图是用若干个全等的等腰梯形拼成的图形,下列说法错误的是( )
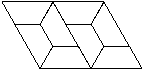 A.梯形的下底是上底的两倍 B.梯形最大角是
A.梯形的下底是上底的两倍 B.梯形最大角是![]()
C.梯形的腰与上底相等 D.梯形的底角是![]()
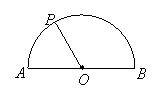 8.如右图,某运动员
8.如右图,某运动员![]() 从半圆跑道的
从半圆跑道的![]() 点出发沿
点出发沿![]() 匀速前进到达终点
匀速前进到达终点![]() ,若以时间
,若以时间![]() 为自变量,扇形
为自变量,扇形![]() 的面积
的面积![]() 为函数的图象大致是( )
为函数的图象大致是( )
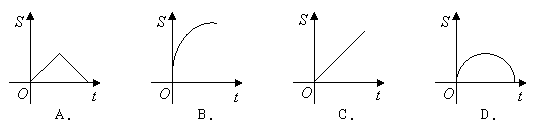 |
二、填空题(本题8个小题,每小题3分,满分24分)
9.计算![]() ___________.
___________.
10.“太阳从西边出来”所描述的是一个___________事件.
11.某校组织学生开展“八荣八耻”宣传教育活动,其中有![]() 的同学走出校门进行宣讲,这部分学生在扇形统计图中应为___________部分.(选择
的同学走出校门进行宣讲,这部分学生在扇形统计图中应为___________部分.(选择![]() ,
,![]() ,
,![]() ,
,![]() 填空)
填空)
 |
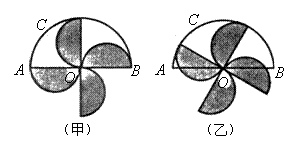
12.中央电视台大风车栏目图标如图甲,其中心为![]() ,半圆
,半圆![]() 固定,其半径为
固定,其半径为![]() ,车轮为中心对称图形,轮片也是半圆形,小红通过观察发现车轮旋转过程中留在半圆
,车轮为中心对称图形,轮片也是半圆形,小红通过观察发现车轮旋转过程中留在半圆![]() 内的轮片面积是不变的(如图乙),这个不变的面积值是___________.
内的轮片面积是不变的(如图乙),这个不变的面积值是___________.
 |
13.已知![]() ,那么:
,那么:![]() ___________.
___________.
14.若双曲线![]() 过两点
过两点![]() ,
,![]() ,则有
,则有![]() ___________
___________![]() (可填“
(可填“![]() ”、“
”、“![]() ”、“
”、“![]() ”).
”).
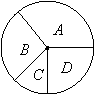
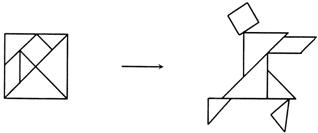
15.用边长为![]() 的正方形材料制作的七巧板拼成一幅土家摆手舞图案,其中舞者头部占整个身体面积的___________.
的正方形材料制作的七巧板拼成一幅土家摆手舞图案,其中舞者头部占整个身体面积的___________.
 |
16.观察一列有规律的数:![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,它的第
,它的第![]() 个数是___________.
个数是___________.
三、解答题(本大题9个小题,满分72分)
17.(本小题6分)
计算:![]() .
.
18.(本小题6分)
已知分式:![]() ,
,![]() .
.![]() .下面三个结论:①
.下面三个结论:①![]() ,
,![]() 相等,②
相等,②![]() ,
,![]() 互为相反数,③
互为相反数,③![]() ,
,![]() 互为倒数,请问哪个正确?为什么?
互为倒数,请问哪个正确?为什么?
19.(本小题6分)
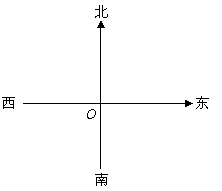 考点办公室设在校园中心
考点办公室设在校园中心![]() 点,带队老师休息室
点,带队老师休息室![]() 位于
位于![]() 点的北偏东
点的北偏东![]() ,某考室
,某考室![]() 位于
位于![]() 点南偏东
点南偏东![]() ,请在右图中画出射线
,请在右图中画出射线![]() ,
,![]() ,并计算
,并计算![]() 的度数.
的度数.
20.(本小题6分)
小明发现把一双筷子摆在一个盘子上,可构成多种不同的轴对称图形,请你按下列要求,各添画一只筷子,完成其中三种图形:
 |
21.(本小题9分)
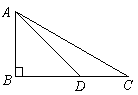 会堂里竖直挂一条幅
会堂里竖直挂一条幅![]() ,小刚从与
,小刚从与![]() 成水平的
成水平的![]() 点观察,视角
点观察,视角![]() ,当他沿
,当他沿![]() 方向前进
方向前进![]() 米到达到
米到达到![]() 时,视角
时,视角![]() ,求条幅
,求条幅![]() 的长度.
的长度.
22.(本小题9分)
我市某生态果园今年收获了![]() 吨李子和
吨李子和![]() 吨桃子,要租用甲、乙两种货车共
吨桃子,要租用甲、乙两种货车共![]() 辆,及时运往外地,甲种货车可装李子
辆,及时运往外地,甲种货车可装李子![]() 吨和桃子
吨和桃子![]() 吨,乙种货车可装李子
吨,乙种货车可装李子![]() 吨和桃子
吨和桃子![]() 吨.
吨.
(1)共有几种租车方案?
(2)若甲种货车每辆需付运费![]() 元,乙种货车每辆需付运费
元,乙种货车每辆需付运费![]() 元,请选出最佳方案,此方案运费是多少.
元,请选出最佳方案,此方案运费是多少.
23.(本小题9分)
初三(1)班男生一次![]() 米短跑测验成绩如下.(单位:秒)
米短跑测验成绩如下.(单位:秒)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
体育老师按![]() 秒的组距分段,统计每个成绩段出现的频数,填入频数分布表,并绘制了频数分布直方图.
秒的组距分段,统计每个成绩段出现的频数,填入频数分布表,并绘制了频数分布直方图.
(1)请把频数分布表及频数分布直方图补充完整.
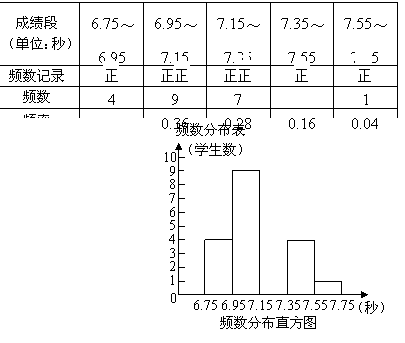 |
(2)请说明哪个成绩段的男生最多?哪个成绩段的男生最少?
(3)请计算这次短跑测验的合格率(![]() 秒及
秒及![]() 秒以下)和优秀率(
秒以下)和优秀率(![]() 秒及
秒及![]() 秒以下).
秒以下).
24.(本小题9分)
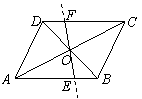 如图,已知
如图,已知![]() 的对角线
的对角线![]() ,
,![]() 相交于点
相交于点![]() ,
,![]() 绕点
绕点![]() 顺时针旋转交
顺时针旋转交![]() ,
,![]() 于
于![]() ,
,![]() .
.
(1)证明:四边形![]() 是平行四边形.
是平行四边形.
(2)![]() 绕点
绕点![]() 顺时针旋转_________度时,平行四边形
顺时针旋转_________度时,平行四边形![]() 为菱形?请说明理由.
为菱形?请说明理由.
25.(本小题12分)
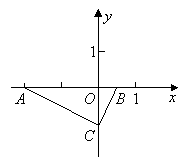
在平面直角坐标系内有两点![]() ,
,![]() ,
,![]() 所在直线为
所在直线为![]() ,
,
(1)求![]() 与
与![]() 的坐标
的坐标
(2)连结![]() ,求证:
,求证:![]()
(3)求过![]() ,
,![]() ,
,![]() 三点且对称轴平行于
三点且对称轴平行于![]() 轴的抛物线解析式
轴的抛物线解析式
 (4)在抛物线上是否存在一点
(4)在抛物线上是否存在一点![]() (不与
(不与![]() 重合),使得
重合),使得![]() ,若存在,请求出
,若存在,请求出![]() 点坐标,若不存在,请说明理由.
点坐标,若不存在,请说明理由.
数学初中毕业学业考试试卷
参考答案及评分标准
说明:
(一)《答案》中各行右端所注分数表示正确作完该步应得的累计分数,全卷满分120分.
(二)《答案》中的解法只是该题解法的一种或几种,如果考生的解法和本《答案》不同,可参照本《答案》中评分标准的精神,进行评分.
(三)评卷时,要坚持每题评阅到底,勿因考生解答有误而中断评阅,如果考生的解答在某一步出现错误,影响后续部分而未改变本题的内容与难度者,视影响程度来决定后面部分的得分,但原则上不超过后面部分满分的一半,如果有严重概念性错误,应不给分.
一、选择题(本题满分24分,每小题3分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答案 | A | B | D | C | B | A | D | C |
二、填空题(本题满分24分,每小题3分)
| 题号 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 答案 |
| 不可能 |
|
|
|
|
|
|
三、解答题(本题满分72分)
17.(6′)解:原式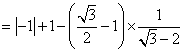 3′
3′
![]() 4′
4′
![]()
![]() 6′
6′
18.(6′)解:![]() 互为相反数正确 2′
互为相反数正确 2′
因为:![]() 3′
3′
![]() 4′
4′
![]() 5′
5′
![]() 6′
6′
19.(6′)解:
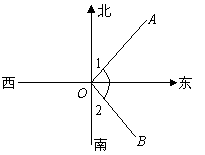
3′
![]()
![]() 6′
6′
20.(6′)
 |
21.(9′)
解:在![]() 中,
中,![]() .
.![]()
![]()
那么:![]() 3′
3′
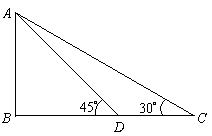 在
在![]() 中,
中,![]()
![]()
![]() 6′
6′
得:![]()
解得:![]() 9′
9′
22.(9′)
解:(1)设安排甲种货车![]() 辆,乙种货车
辆,乙种货车![]() 辆, 1′
辆, 1′
根据题意,得:![]()
![]() 3′
3′
![]() 取整数有:3,4,5,共有三种方案. 4′
取整数有:3,4,5,共有三种方案. 4′
(2)租车方案及其运费计算如下表.(说明:不列表,用其他形式也可)
| 方案 | 甲种车 | 乙种车 | 运费(元) |
| 一 | 3 | 3 |
|
| 二 | 4 | 2 |
|
| 三 | 5 | 1 |
|
8′
答:共有三种租车方案,其中第一种方案最佳,运费是5100元. 9′
23.(9′)解:
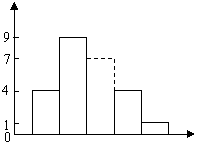 (1)(在图表上完成)
(1)(在图表上完成)
| 成绩段 | |||||
| 频数记录 | |||||
| 频数 | 4 | ||||
| 频率 | 0.16 |
3′
(2)6.95~7.15(秒)段人数最多.7.55~7.75(秒)段人数最少. 6′
(3)合格率![]()
优秀率![]() 9′
9′
24.(9′)
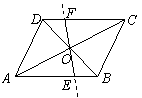 (1)证明:
(1)证明:![]() 四边形
四边形![]() 是平行四边形
是平行四边形
![]()
![]() 2′
2′
![]() 3′
3′
又![]() 4′
4′
![]() 5′
5′
![]() 且
且![]()
![]() 四边形
四边形![]() 是平行四边形 6′
是平行四边形 6′
(2)![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 度时,平行四边形
度时,平行四边形![]() 是菱形 7′
是菱形 7′
证明:![]() 四边形
四边形![]() 是平行四边形
是平行四边形
又![]()
![]() 8′
8′
![]() 平行四边形
平行四边形![]() 是菱形. 9′
是菱形. 9′
25.(12′)
(1)以![]() 代入
代入![]()
![]() 2′
2′
得:![]() 则有
则有![]() 3′
3′
(2)![]()
![]() 5′
5′
![]() 6′
6′
(3)设抛物线的解析式为![]() ,以三点的坐标代入解析式得方程组:
,以三点的坐标代入解析式得方程组:
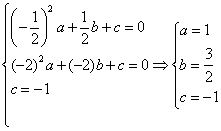 8′
8′
所以![]() 9′
9′
(4)假设存在点![]() 依题意有
依题意有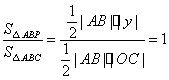 ,
,
得:![]() 10′
10′
①当![]() 时,有
时,有![]() 即
即![]()
解得:![]() 11′
11′
②当![]() 时, 有
时, 有![]() ,即
,即![]()
解得:![]() (舍去),
(舍去),![]()
![]() 存在满足条件的点
存在满足条件的点![]() ,它的坐标为:
,它的坐标为:
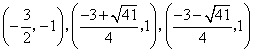 12′
12′