九年级数学第24章测试题
班级 学号 姓名 .
一、选择题:(每题3分,共30分)
1.下列说法中正确的个数为( )
(1)所有的等边三角形都全等; (2)两个三角形全等,它们的最大边是对应边
(3)两个三角形全等,它们的对应角相等; (4)对应角相等的三角形是全等三角形
A.1 B.2 C.3 D.4
2.下列说法中,错误的是( )
A.全等三角形的面积相等; B.全等三角形的周长相等
C.面积相等的三角形全等; D.面积不等的三角形不全等
3.在△ABC和△A′B′C′,如果满足条件( ),可得△ABC≌△A′B′C′.
A.AB=A′B′,AC=A′C′,∠B=∠B′; B.AB=A′B′,BC=B′C′,∠A=∠A′
C.AC=A′C′,BC=B′C′,∠C=∠C′; D.AC=A′C′,BC=B′C′,∠B=∠B′
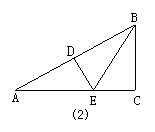4.如图(1)所示,已知AB=CD,AD=CB,AC、BD相交于O,则图中全等三角形有( )
A.2对 B.3对
C.4对 D.5对
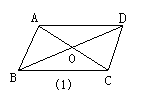
5.如图(2)所示,在△ABC中,∠C=90°,DE⊥AB于D,BC=BD,结果AC=3cm,那么AE+DE=( )
A.2cm B.3cm C.4cm D.5cm
6.下列命题中,是假命题的是( )
A.矩形的对角线相等 B.圆是轴对称图形； C.三点确定一个圆
D.从圆外一点引圆的两条切线,它们的切线长相等
7 .将命题“对顶角相等”写也“如果……,那么……”的形式,正确的是( )
A.如果两个角相等,那么它们是对顶角； B.如果两个角是对顶角,那么它们相等
C.如果对顶角,那么相等； D.如果两个角不是对顶角,那么这两个角不相等
8.对假命题“任何一个角的补角都不小于这个角”举反例,正确的反例是( )
A.∠α=60°,∠α的补角∠β=120°,∠β>∠α；
B.∠α=90°,∠α的补角∠β=90°,∠β=∠α
C.∠α=100°,∠α的补角∠β=80°,∠β<∠α； D.两个角互为邻补角
9. 只用无刻度直尺就能作出的是( )
A.延长线段AB至C,使BC=AB; B.过直线L上一点A作L的垂线
C.作已知角的平分线; D.从点O再经过点P作射线OP
10.下列画图语言表述正确的是( )
A.延长线段AB至点C,使AB=BC; B.以点O为圆心作弧
C.以点O为圆心,以AC长为半径画弧; D.在射线OA上截取OB=a,BC=b,则有OC=a+b
二、填空题:(每题3分,共24分)
1、如图，直线AB、CD被EF所截，已知∠1=∠2,求证：AB∥CD。
证明：∵∠2=∠3，（ ），∠1=∠2（已知） ∴ ∠1=∠3∴ AB∥CD（ ）
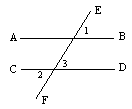
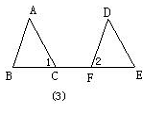
2、如图3所示,点C、F在BE上,∠1=∠2,BC=EF,请补充条件:___________(写出一个即可),使△ABC≌△DEF.
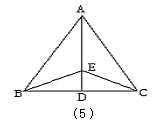
3、如图5所示,已知AB=AC,EB=EC,AE的延长线交BC于D,那么图中的全等三角形共有__________对.
(6) (8)
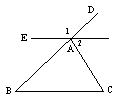
4、如图6，已知点B、A、D在同一直线上，AE∥BC，∠1=150°，∠C=70°，则∠BAC=
度。
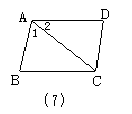
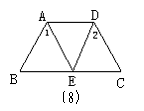
5、如图7,AB=DC,AD=BC,∠1=68°,∠2=41°,则∠B的度数是______.
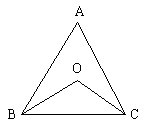
6、如图8，ΔABC中，∠A=50°，BO、CO分别是∠ABC、∠ACB的平分线，则∠BOC的度数是 度。
7、请在横线上填上一个适当的条件或结论,使所得的命题是真命题：如果⊙O1的半径为R=5cm,⊙O2的半径为r=3cm,当O1O2=______cm时, ⊙O1与⊙O2相交.
8、下列语句中：① 同角的补角相等；② 雪是白的；③ 画∠AOB=∠α;④ 他是小张吗？⑤两直线相交只有一个交点。其中是命题的有 (填序号)
三、解答题:(共46分)
1、把下列命题改写成“如果……那么……”的形式。（9分）
（1）平行于同一条直线的两直线平行。
改：
（2）为相反数的两数它们的绝对值相等。
改：
（3）两条互相垂直的直线夹角为直角。
改：
2、尺规作图：（要求不写作法，保留作图痕迹）（8分）
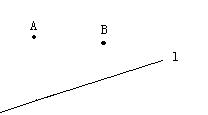
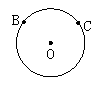
（1）如图所示,已知B、C是⊙O上的两点. 已知Ａ、Ｂ两点和直线ｌ，
求作⊙O上一点P,使得PB=PC. 求作⊙Ｏ， 使⊙Ｏ经过Ａ、Ｂ两点，且圆心在直线Ｌ上
 |
3.完成以下证明,并在括号内填写理由:（6分）
已知:如图8所示,AB∥DE,∠1=∠2.
求证:AE∥DC.
证明:∵ AB∥DE( ),
∴ ∠1=∠AED( ),
∵ ∠1= ∠2( ),
∴ ∠2=∠_______( ),
∴
AE∥DC(
).
4、如图．AB＝CD, ∠D＝∠ECA, EC＝FD，求证：AE＝BF (7分)
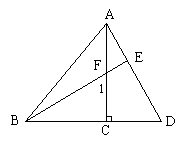5、如图，已知AC⊥BD于C，CF=CD，BF的延长线交AD于点E，且AC=BC。求证：（1）∠1=∠D；（2）BE⊥AD。(8分)
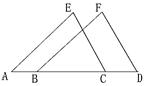
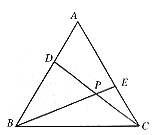6. 已知：如图，在等边三角形ABC中，D、E是AB、AC上的点，且AD＝CE，若CD与BE交于P点。
求证：∠DPB＝60°。(8分)