九年级数学第二学期第一次月考试题

 

九年级数学第二学期第一次月考试题

题 号	一	二	三	四	五	六	七	八	总　分
得 分

一、一一对应，对号入座(每小题4分，共40分)

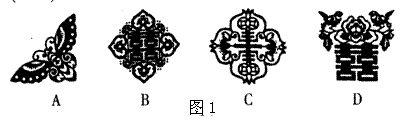
1. 我国文化宝库中有很多优秀遗产，剪纸艺术就是其中之一，且在民间广泛流传，浮山县的民间剪纸乃国内之精华，享誉中外．下面的一组剪纸作品(如图1)，属于中心对称图形的是(　　 )．

2. 2006年春节期间，为了促销商品，甲、乙两个超市都采取优惠措施，甲超市推出八折后再打八折，乙超市则一次性六折优惠，若同样价格的商品，下列结论正确的是(　　 )．

　 A．甲比乙优惠　 B．乙比甲优惠　 C．两超市优惠条件一样　D．无法比较

3. 下列说法正确的是(　　 )．

　 A．5的平方根是　 　　　　　　B．若,则a<O

C．若，则a>O　 　　　　　D．

4. 为了筹备班级的初中毕业联欢会，班长对全班学生爱吃哪种水果做了民意调查，那么决定最终买什么水果时，下面的调查数据中最值得关注的是 (　　 )．

　 A．中位数　　　　B．平均数　　　　C．众数　　　　D．方差

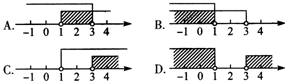5. 不等式组的解集在数轴上可表示为(　　 )

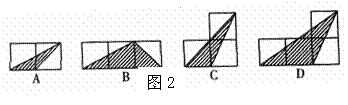
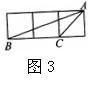
6. 已知小正方形的边长为1，则图2

中的三角形(阴影部分)与图3中△ABC相似的是(　　)．

　　　　　　　　　 

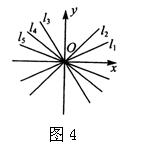
7. 如图4，在一直角坐标系中，一次函数的图象分别为，则下列关系中正确的是(　　 )．

A．<<<<　　　　 B．<<<<

C．<<<<　　　 D．<<<<

　　　　　　　　　　　　　　　　　　　　　　　　　

8. 下列说法正确的是(　　)．

　 A．若A(—1，a²)与B(b，1)关于y轴对称，则a+b=2．

B．若a>0,则二次根式与是同类二次根式．

C．无论a取什么值，方程ax²-2x-a=0总有两实数根．

　 D．若关于x的一次函数y=(k-1)x-3的图象不经过第一象限，则k<1.

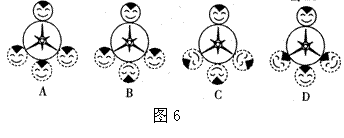
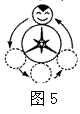
9. 一电动玩具的正面是由半径为r的小圆盘和半径为2r的大圆盘依图5方式连接而成的．小圆盘在大圆盘的圆周上外切滚动一周且不发生滑动(大圆盘不动)，回到原来的位置．在图6中，虚线所示位置的三个圆内，所 画的头发、眼睛、嘴巴位置正确的是(　　)．

10.如图7,在正方形铁皮上剪下一个圆形和扇形,使之恰好围成如图所示的一个圆锥模型.设圆的半径为r，扇形半径为R，则圆的半径与扇形半径的关系为（　　）

A．R=2r　　　　B．R=r　　　 　 C．R=3r　　　　 D．R=4r　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

二、开心填一填(每小题4分，共20分)

11.若小明家元月份收入2300元，记作+2300元，则开支1200元，记作_________　.

12. 据查阅有关资料，我国因环境污染造成的巨大经济损失，每年高达681 000 000元，这个数据用科学记数法表示为________________　.

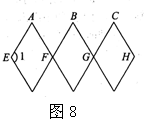
13.如图8，是一个根据四边形的不稳定性制作的边长均为18cm的可活动菱形衣架．若墙上钉子之间的距离AB=BC=18 cm，则∠1=_______ 度

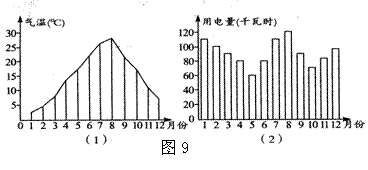
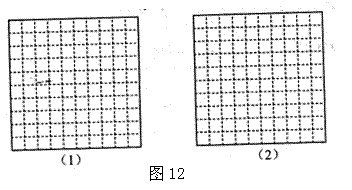
14.图9(1)表示某地区2005年12个月中每月的平均气温，图9(2)表示该地区某家庭这年12个月中每月的用电量．根据统计图，请你说出该家庭用电量与气温之间的关系(只要写出一条信息即可)：________________________________　　　　　 　　　　　　

　 __________________________________________________________________.

　　　　　　　　　　　　　　　　　　　

图10

15.尚俊家2006年元月买了一辆大客车，每到下雨时，他就观察启动后的雨刷器(用来刷去汽车前方挡风玻璃上雨水的装置)．如图10是他家汽车的一个雨刷器的示意图，雨刷杆AB与雨刷CD在B处固定连接(不能转动)，当杆AB绕A点转动90°时，雨刷CD扫过的面积有多大呢?为了回答他自己提出的问题，作了如下测量：CD=79cm，∠DBA=20°，端点C、D与点A的距离分别是105 cm、35cm．他经过认真思考计算出了结果，你知道尚俊怎样计算的吗?也请你算一算雨刷CD扫过的面积为__________ cm².

三、用心想一想(分) （本题满分16分，共2小题，每小题8分）

16.解方程：

17.（用数学眼光看世界：）海门市三星镇的叠石桥国际家纺城是全国最大的家纺专业市场，年销售额突破百亿元．某天，该家纺城的羽绒被和羊毛被这两种产品的销售价分别为415元/条、150元/条．现购买这两种产品共80条，付款不超过2万元，问最多可购买羽绒被多少条?

四、（本题满分16分，共2小题，每小题8分）

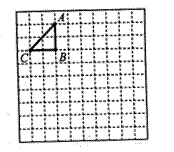
18.图11是一个10×10的正方形网格(小正方形边长为1)，△ABC是格点三角形(顶点为小正方形的顶点)，请你完成下面的两个题目.

(1)在图11中画出与△ABC相似的格点△A₁B₁C₁和△A₂B₂C₂ ,且=8,=1

(2)在图12中用与△ABC、△A₁B₁C₁和△A₂B₂C₂全等的格点三角形(每一个三角形至　　少用一次)，拼一个轴对称图形和一个中心对称图形.

	图11

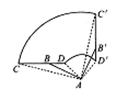
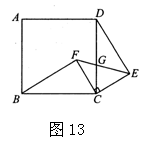19.如图13，四边形ABCD是正方形，△ECF是等腰直角三角形，其中CE=CF，G是CD与EF的交点.

(1)求证：BF=DE；

(2)若BC=5，CF=3,∠BFC=90°,求的值.

　　　　　　　　　　　　　　　　　　　　　　　　　　  　

五、（本题满分20分，共2小题，每小题10分）

20.阅读下列材料，解答后面问题．

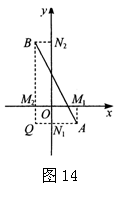
在平面直角坐标系中，已知x轴上两点A(x₁，0)，B(x₂，0)的距离记作AB= x₁-x₂．如A(x₁，y₁)，B(x₂，y₂)是平面上任意两点，我们可以通过构造直角三角形来求A，B间距离.如图14，过A,B分别向x轴 ，y轴作垂线AM₁，AN₂和BM₂,　BN₂,垂足分别是M₁(x₁，0)，N₁(0，y₁，)，M₂(x₂，0)，N₂(0，y₂)，直线AN₁与BM₂交于Q.在Rt△ABQ中，AB²=AQ²+QB².

∵AQ=M₁M₂=x₁-x₂,QB=N₁N₂y₂-y₁　 ∴AB²=x₂-x₁²+y₂-y₁²

由此得任意两点A(x₁，y₁)，B(x₂,y₂) 间距离公式

(1)直接运用平面内两点距离公式，求点A(1，-3)、B(-2，1)之间的距离；

(2)若x轴上有一点C(x₀，0)，则代数式最小值.

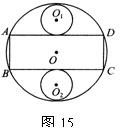21.现有一块直径为2m的圆形铁片，若将它做成一个有盖的油桶，并尽可能的用好这块铁片，工人师傅在圆形铁片上截取两个圆(即两底)和一个矩形(侧面)，如图15所示

(1)若把BC作油桶的高，则油桶的底面半径R₁等于多少?

(2)当把AB作油桶的高时，油桶的底面半径R₂与(1)中的

R₁相等吗?若相等，请说明理由；若不相等，请求出R₂.

		图15

六、（本题满分12分）

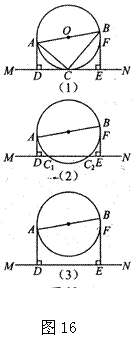22.已知：如图16(1)，直线MN和⊙O切于点C，AB是⊙O的直径，AD⊥MN于O，BE⊥MN于E，交⊙O于F．连结AC、BC．

(1)求证：△ADC∽△CEB；

(2)若AD=m，DE=n，BE=p，试判断n²与4mp的大小关系；

(3)如图(2)，将直线MN向上平移至与⊙O相交时，m、n、p

之间有么关系?如图(3)将直线MN向下平移至与⊙O相离，

m、n、p之间有什么关系?(直接写出结果，不需说明理由．)

七、（本题满分12分）

23.某私营玩具厂招工广告称：“本厂工人工作时间：每天工作8小时，每月工作25天；待遇：熟练工人按计件付工资，多劳多得，计件工资不少于1000元，每月另加福利工资100元，按月结算……”．　 该厂只生产两种玩具：小狗和小汽车，熟练工人晓凤一月份领工资1145元，她记录了如下一些数据：

小狗件数 （单位：个）	小汽车数 （单位：个）	总 时 间 （单位：分钟）	计件工资 （单位：元）
1	1	35	2.8
2	2	70	5.6
3	2	85	6.6

(1)根据表格中的信息，试求出做1个小汽车所需时间和计件工资各是多少?

(2)设晓凤某月生产小狗x个，小汽车y个，月工资(计件工资+福利工资=月工资)为W元．试求W与x的函数关系式.(不需写出自变量x的取值范围)

(3)有一天，厂方从销量方面考虑，对生产作了调整：每个工人每月生产小狗的个数不少于生产小汽车个数的2倍，假设晓凤的工作效率不变，且服从厂家安排，请运用数学知识说明厂家招工广告是否有欺诈行为．

八、（本题满分14分）

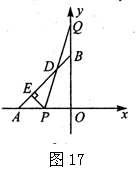
24.如图17，A、B两点的坐标分别为(—3，0)、(0，3)，C点在x轴的正半轴上，且到原点的距离为1.点P、Q分别从A、B两点同时出发，以相同的速度分别向x轴、y轴的正方向作匀速直线运动，直线PQ交直线AB于D.

(1)求经过A、B、C三点的抛物线及直线AB的解析式；

(2)设AP的长为m，△PBQ的面积为S,求出S关于m函数关系式；

(3)作PE⊥AB于E，当P、Q运动时，线段DE的长是否改变?若改变请说明理由，若改变，请求出DE的长；

(4)有一个以AB为边，且由两个与△AOB全等的三角形拼结而成的　 ABST，试求出T点的坐标(画出图形，直接写出结果，不需求解过程)．