九年级数学第三次月考试卷
（考试时间：90分钟 试卷总分：120分）
一、选择题（每小题3分，共15分）
1．据统计，2006年春节期间，云南省石林风景区接待中外游客的人数为
人次，这个数字用科学记数法可表示为（ ）
Ａ．
Ｂ．
Ｃ．
Ｄ．
2．下列运算中正确的是（ ）
Ａ．
Ｂ．
Ｃ．
Ｄ．
3．下面是一天中四个不同时刻两个建筑物的影子：
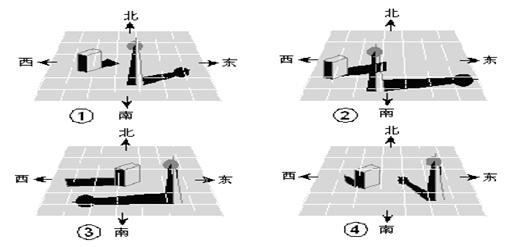
将它们按时间先后顺序进行排列，正确的是 （ ）
Ａ．③④②① Ｂ． ②④③① Ｃ．③④①② Ｄ． ③①②④
4．反比例函数的图象在第一象限内经过点
，过点分别向
轴，
轴引垂线，垂足分别为
，已知四边形
的面积为
，那么这个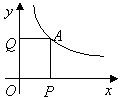
反比例函数的解析式为（ ）
Ａ．
Ｂ．
Ｃ．
Ｄ．
5．一个三角形的两边长为3和6，第三边的边长是方程
的根，则这个三角形的周长是（ ）
Ａ．11 Ｂ．11或13 Ｃ．13 Ｄ．11和13
二、填空题（每小题4分，共20分）
6.
的相反数为_________。
7. 不等式13-3x＞0的正整数解是__________。
8.某同学的身高为1.6米，某一时刻他在阳光下的影长为1.2米，与他相邻的一棵树的影长为3.6米，则这棵树的高度为 米。
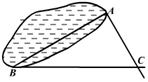
9．如图，为了求出湖两岸A、B两点间的距离，观测者从测点A、B分别测得∠BAC＝
°，∠ABC＝
°，又量得BC＝
，则A、B两点间的距离为 
。
10.
在某数学小组的活动中，组长为大家出了一道函数题：这是一个反比例函数，并且随的增大而减小.请你写出一个符合条件的函数表达式_ ___。
三、解答题（本题共5小题，每小题6分，共30分）
11.
先化简，再求值：（
）÷
，其中x=2005
12.解方程：
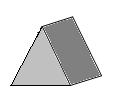
13. 画出如图中实物的三种视图．
14.
已知正比例函数
与反比例函数
的图象都经过点
，
，求这两个函数关系式．
15．列一元二次方程解应用题：
甲公司前年缴税40万元，今年缴税48.4万元。该公司缴税的年平均增长率为多少？
四、解答题（本题共4小题，每小题7分，共28分）
16.如图，晚上，小亮在广场上乘凉．图中线段
表示站立在广场上的小亮，线段
表示直立在广场上的灯杆，点
表示照明灯．
(1)请你在图中画出小亮在照明灯
照射下的影子；
(2)
如果灯杆高
12m，小亮的身高
m，小亮与灯杆的距离
m，请求出小亮影子的长度．
（第16题图）
17.
已知一次函数
与反比例函数的图象在第一象限的交点为
。（1）求
及的值；
（2）求一次函数的图象与两坐标轴的交点坐标．
18.在□ABCD中，
，
为
的中点，
与
延长相交于点
．
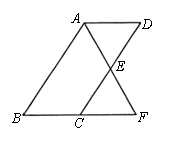求证：
．
19.
甲、乙两个工程队分别同时开挖两段河渠，所挖河渠的长度
与挖掘时间
之间的关系如图所示，请根据图象所提供的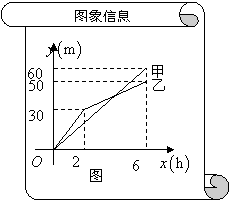
信息解答下列问题：
（1）乙队开挖到30m时，用了 h．
开挖6h时甲队比乙队多挖了 m；
（2）请你求出：
①甲队在
的时段内，与之间的函数关系式；
②乙队在
的时段内，与之间的函数关系式；
五．解答题（本题共3小题，每小题9分，共27分）
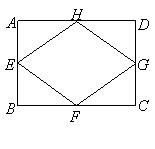20. 如图，已知
是矩形
各边中点．
求证：四边形
为菱形．
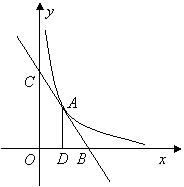21.直线
与双曲线只有一个交点
，且与轴、轴分别交于
两点，
垂直平分
，垂足为
，求直线、双曲线的解析式．
22.制作一种产品，需先将材料加热达到60℃后，再进行操作．设该材料温度为（℃），从加热开始计算的时间为（分钟）．据了解，该材料加热时，温度与时间成一次函数关系；停止加热进行操作时，温度与时间成反比例关系（如图）．已知该材料在操作加工前的温度为15℃，加热5分钟后温度达到60℃．
（1）分别求出将材料加热和停止加热进行操作时，与的函数关系式；
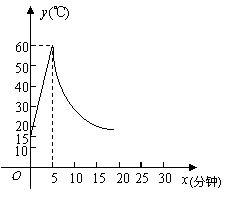（2）根据工艺要求，当材料的温度低于15℃时，须停止操作，那么从开始加热到停止操作，共经历了多少时间？