九年级数学练习题（三）
（考试时间120分钟，满分150分） 姓名：
一、选择题（每小题3分，共30分）
1．现规定一种新运算，a▲b=a-b，则（－3）▲（－2）=（ ）
A．6 B．－6 C．－9 D．9
2．在下列实数中：
、
、
、
、0.101001中，无理数有（ ）个
A．1 B．2 C．3 D．4
3．如果x+y=5，xy=6，则
=（ ）
A．13 B．
C．
D．
4．点A（2，0）、B（－
，0）、C（0，1），以A、B、C三点为顶点画平行四边形，则第四个顶点不可能在（ ）象限
A．一 B．二 C．三 D．四
5．下图①表示的是组合在一起的模块,在②③④⑤四个图中,这个模块的俯视图是（ ）
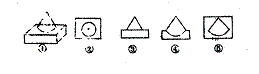
A．⑤ B．② C．③ D．④
6．某城市进行旧城区人行道的路面翻新，准备对地面密铺彩色地砖，有人提出了4种地砖的形状供设计选用：①正三角形，②正四边形，③正五边形，④正六边形。其中不能进行密铺的地砖的形状是（ ）
A．① B．② C．③ D．④
7．两圆的半径R、r分别是方程x2－3x+2=0的两根，且圆心距为d=3，则两圆的位置关系是（ ）
A．相切 B．内切 C．外离 D．相交
8．如图，同心圆中，两半径分别为2、1，∠AOB=120°，则阴影部分的面积为（ ）
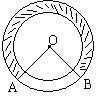A．4π B．2π C．
D．π
9．甲、乙、丙、丁四人的数学测验成绩分别为90、90、x、80
这组数据的众数与平均数恰好相等，这组数据的中位数是（ ）
A．100 B．95 C．90 D．85
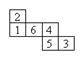10．在一个均匀的正方体六个面上分别标有数1、2、3、4、5、6，右图是这个正方体表面的展开图，抛掷这个正方体，则朝上一面上的数恰好等于朝下一面上的数的的概率是（ ）
A．
B． C． D．
二、填空题（每小题4分，共40分）
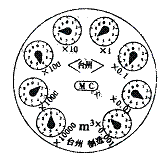
11．小苏家的水表如图所示，该水表的读数是 （精确到0.1）
12．因式分解：2x2－8=
若x2－5x+m=(x－3)(x＋n)，则m= n=
13．要使代数式
有意义，则x的取值范围是
，在此条件下，化简
=
14．课外阅读课上，老师将43本书分给各小组，每组8本，还有剩余；每组9本，却不够分，则有几个小组
15．如图，弹簧总长y(cm)与所挂物体质量x(kg)之间是一次函数关系。则该弹簧不挂物体时的长度为
16．已知抛物线y=ax2+bx+c经过A（－2，7）、B（6，7）、C（－3，－8），则该抛物线上纵坐标为－8的另一个点的横坐标是
17．如图，已知圆心角∠AOB的度数为100°，则圆周角∠ACB=
18．如图，梯形ABCD中，AB∥CD，E为BC中点，使△DEA的面积为S1，梯形ABCD的面积为S2，则S1与S2的关系是
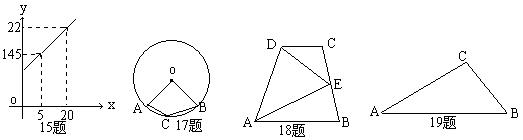19．如图，在一张比例尺为1：100000的地图上，测得∠A=30°，∠B=45°，AC=2cm，则在实际中，△ABC的面积=
（
，
，保留2个有效数字）
20、印制一本书，为了使装订成书后页码恰为连续的自然数，可按如下方法操作，先将一张整版的纸对折一次为4页,再对折一次为8页，连续对折3次为16页……，然后再排页码。如果想设计一本16页的纪念册，请你按图1、图2、图3（图中的1、16表示页码）的方法折叠，在图4中填上按这种折叠方法得到的各页在该面相应位置上的页码。
三、解答题（共80分）
21．先化简,再求值：
22．解方程
(10分)
其中x=sin30° y=tan60°（10分）
23．已知关于x的方程x2－2(m+1)x+m2=0
⑴当m取什么值时，原方程没有实数根
⑵对m选取一个合适的非零整数，使原方程有两个实数根，并求这两个实数根的平方和。（12分）
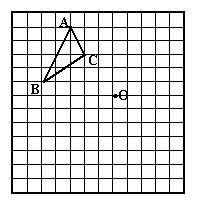
24．在下面的网格图中按要求画出图开，并回答问题：
⑴先画出△ABC向下平移5格后的△A1B1C1，再画出△ABC以点O为旋转中心，沿顺时针方向旋转90°后的△A2B2C2；
⑵如图，以点O为原点建立平面直角坐标系，试写出点A2、B1的坐标。（12分）
25．为配合新课程的实施，某市举行了“应用与创新”知识竞赛，共有1万名学生参加了这次竞赛（满分100分，得分全为整数）。为了了解本次竞赛成绩的情况，从中随机抽取了部分学生的竞赛成绩，进行统计，整理见下表。
| 组别 | 分组 | 频数 | 频率 |
| 1 | 49.5—59．5 | 60 | 0.12 |
| 2 | 59.5—69.5 | 120 | 0.24 |
| 3 | 69.5—79.5 | 180 | 0.36 |
| 4 | 79.5—89.5 | 130 | c |
| 5 | 89.5—99.5 | b | 0.02 |
| 合 计 | a | 1.00 | |
解答下列问题：
⑴在这个问题中，总体是 ，样
本容量a=
⑵第四小组的频率c=
⑶被抽取的学生成绩的中位数落在第几小
组内？
⑷若成绩在90分上(含90分)的学生获一等奖，
请你估计全市获一等奖的人数 (12分)
26．如图,等腰梯形ABCD中，AB∥CD,AD=BC，延长AB到E，使BE=CD，连结CE，
⑴求证：CE=CA
⑵作一个⊙O使其过A、C、E三点，并判断CD是否是⊙O的切线（不予证明）
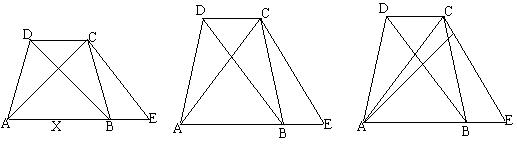⑶上述条件下,若AF⊥CE于F,且AF平分∠DAE,
，求sin∠CAF的值。(12分)
27．已知一个二次函数的图象经过A（－1，1）、B（0，3）、C（4、－5）三点，
⑴求这个函数的解析式及顶点D的坐标。
⑵这个函数的图象与x轴有两个交点，除点A外的另一个交点设为E，在△AOB和△BOE、△ABE、△DBE中，是否有相似的三角形，如果有，指出哪几对三角形相似，并加以证明。如果没有，说明理由。（12分）