九年级数学练习题（一）
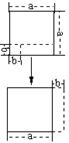
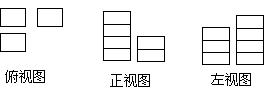
| 一、选择题（每小题3分，计30分） 1．计算 A．8 B．－10 C．－ 2．下列变形是因式分解的是（ ） A． B． C． D． 3、一张桌子重叠摆放了若干枚大小、形状完全相同的麻将，它的三视图如图所示，则这张桌子共摆放有麻将（ ）枚。 A．9 B．11 C．12 D．13 4．从边长为a的正方形内去掉一个边长为b的正方形，然后将剩余部分剪拼成一个矩形，上述操作可验证的等式是（ ）。 A． B． C． D．
A．a＜3 B．a=1 C．a=－1 D．a＞3 6．绵阳市中考结束后，高中录取新生主要依据考生的总分，这与下面哪个量的关系较大？答（ ） A．平均数 B．中位数 C．众数 D．方差 7．下列调查最适合普查方式的是（ ） A．夏季准饮市场上冰淇淋的质量情况 B．对中考学生的数学试卷答题情况进行分析 C．你所在班级的同学的身高情况 D．绵阳市一月的流动人口情况
点P从起点A出发，沿ABCD向点 D匀速运动，设运动时间为t ,以点P、 A、D为顶点的三角形面积为y，y随 x的变化而变化，在下列图象中，能正 确反映y与x的函数关系是（ ）
① ③ A．1 B．2 C．3 D．4
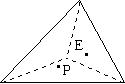
A．1个 B．2个 C．3个 D．4个 二、填空（每小题分，计分） 11．“神舟”六号在太空中的飞行速度是7.9千米/秒，它在空中飞行了115小时32分钟，用科学记数法表示出它在空中飞行了大约 千米。（保留三个有效数字） 12．按照一定顺序排列的一列数叫数列，一般用a1、a2、a3、a4……an-1、an表示一列数，又简记为{an}。现在数列{an}满足一个关系式： 13．在平面直角坐标系中，点A（－3，0）点B（0，3），分别以A、B为圆心，2和3的半径作圆，则两圆位置关系为 。 14．如图，一只蚂蚁从一边长为2的正三棱锥的底面中心P爬到它的一侧面的中心E，则它爬过的最短距离是 。
15．如图，在△ABD和△ACE中，有下列四个论断：①AB=AC ②AD=AE ③∠B=∠C ④BD=CE，请以其中三个论断为条件，余下一个论断作为结论，写出一个真命题： 。 16．随着计算机技术的迅猛发展，电脑价格不断降低，某品牌电脑按原售价降低m元后，又打8折，现售价为n元，那么该电脑的原售价为 。 17．不等式组 18．等腰△ABC中，AB=6，BC、AC的长是关于x的方程x2－10x+m=0的两根，则m的值是 。 三、解答题 19．（本小题2个小题，每小题8分，计16分） ⑴计算： ⑵先化简分式， 20．下面是同学们玩过的“石头、剪刀、布”的游戏规则：游戏在两位同学之间进行，用伸出的拳头表示“石头”，伸出食指和中指表示“剪刀”，伸出手掌表示“布”，两人同时口念“石头、剪刀、布”，一念到“布”时，同时出手，“布”赢“石头”，得3分，“石头”赢“剪刀”，得5分，“剪刀”赢“布”得2分。 ⑴小明和小华玩此游戏过程中，小明赢了12次，得72分，其中“剪刀”赢“布”7次，聪明的你请用学过的数学知识求出小明“布”赢“石头”，“石头”赢“剪刀”各多少次？ ⑵若小明与小华玩了此游戏后，重新规定：若每种赢法得分相相同，同种手势不分胜负继续比赛，假定两人每次都是“等可能”地做三种手势，那么一次比赛时，两人做同种手势（即不分胜负）的概率是多少？请用树状图方法解答。 21．如图，直线y=2x+2与x、y轴分别相交于两点A、B，将△AOB绕点O顺时针旋转90°得到 △A′OB′。 ⑴在图中画出△A′OB′。 ⑵求过A、A′、B′三点的抛物线的解析式。 22．如图，在△ABC中，CE平分∠ACB，且AE⊥CE于E，点F是AB的中点，连结EF。 ⑴求证：EF∥BC。 ⑵若AB=7，BC=8，AC=
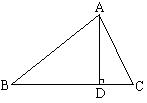
23．如图，在△ABC中，AD是BC边上的高，tanB=cos∠DAC ⑴求证：AC=BD。 ⑵若sinC=
24．先阅读下面材料再完成后面问题。 过抛物线y=ax2(a>0)的对称轴上一点（0，－ 问题：若直线y=kx+b交抛物线 ⑴求抛物线 ⑵求证：直线AB过焦点F时，CF⊥DF ⑶在条件（2）下，当直线AB过点
25．已知：点A在以O为原点的数轴上，点P在数轴的上方，PO=PA=2，∠MPN绕点P旋转，射线PM交数轴于点C，射线PN及其反向延长线PN′交数轴于点B，点C、A、B的对应实数分别为x、a、b，且y=b-a ⑴右∠OPA=40°，∠MPN=110°，当点C位于原点左侧时，如图1求证：△COP∽△PAB，并求y与x之产的函数关系式（不写自变量的取值范围） ⑵若∠OPA=40°，∠MPN=110°，当点C位于原点右侧时，（1）求的函数关系式是否成立，请说明理由，如图（2）
| 此题考察学生的基本运算能力 八年级上89页练习第1页改编,着重考查因式分解的定义 本题改编于七年级上132页，试一试，着重考查学生对三视图的理解能力和空间想象能力 八年级上94(84)页课题学习改编，着重考查擦图形面积间的转换 此题重在考察不等式的基本性质 七年级下108页想一想改编 八年级下61页第九题改编，考察数形结合思想 改编于八年级下81页第1题，着重考查学生对相似三角形性质的理解（相似三解形对应边成比例） 改编于八年级上38页练习1题，查考学生的识图能力，平行四边形的识别方法；会运用“猜想验证”的方法解决问题。 与现实相连考查科学记数法。 与高中知识衔接，考查阅读理解。 考查圆与圆的位置关系。 考查侧面展开图。 考查三角形全等，改编于九年级上90页习题24.2第1题。 考查学生根与系数关系和分类思想。 改编于八年级下14页练习第2题(3)与18页4题(2)，考查学生的计算能力。 改编于九年级上12页2题（4） 改编于九年级上127页问题2。 函数与旋转相结合。 改编于九年级下61页8题。 改编于八年级下121页16题。 与高中函数知识衔接。考查学生阅读理解能力和自学能力。 考查三角形相似与函数的关系。体现出从特殊到一般的数学思想。 |
的值为（ ）
D．
5．若关于x的不等式（a－3）x＜－2的解集为x＞1，则实数a满足的条件是（ ）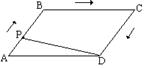
8．如下图，在平行四边形ABCD中，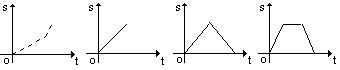
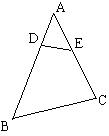9．如图，在△ABC中,∠ADE=∠C,则下列等式成立的有（ ）个
②
④
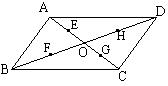10．如图，在平行四边形ABCD中，已知两条对角线相交于O、E、F、G、H分别是AO、BO、CO、DO的中点，以图中的各点为顶点，可以画出的平行四边形的个数是（ ）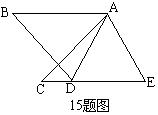
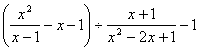(n=1、2、3、……n)且a1=2。根据已知条件计算出a2、a3、a4的值，然后进行归纳猜想an= 。（用n的代数式表示）
的整数解 。
并从x=1，－1，0中选出适合原式的x，求值。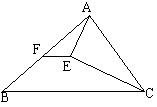
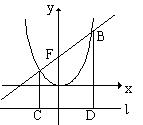，请选取以上条件求EF的值。
，BC=12，求AD的长。
）作对称轴的垂线，则抛物线上任意一点P到点F（0，
于A、B、AC、BD垂直与抛物线的准线l，垂足分别为C、D。
（－1，0）时，求这条直线对应的函数解析式。
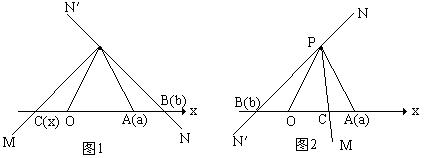⑶若∠OPA=
，∠MPN=
（90°＜