概率初步单元检测
班级 学号 姓名 得分
一、选择题（每题4分，共32分）
1． 下列事件是必然事件的是 （ ）
A． 明天天气是多云转晴
B． 农历十五的晚上一定能看到圆月
C． 打开电视机，正在播放广告
D． 在同一月出生的32名学生，至少有两人的生日是同一天
2． 下列说法中正确的是 （ ）
A． 可能性很小的事件在一次实验中一定不会发生
B． 可能性很小的事件在一次实验中一定会发生
C． 可能性很小的事件在一次实验中有可能发生
D． 不可能事件在一次实验中也可能发生
3． 在10000张奖券中，有200张中奖，如果购买1张奖券中奖的概率是（ ）
A．
B．
C． 
D．
4． 一个袋子中有4个珠子，其中2个是红色，2个蓝色，除颜色外其余特征均相同，若在这个袋中任取2个珠子，都是红色的概率是 （ ）
A．
B．
C． 
D．
5． 有5条线段的长分别为2、4、6、8、10，从中任取三条能构成三角形的概率是（ ）
A．
B．
C．
D．
6．
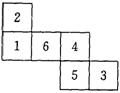
一个均匀的立方体六个面上分别标有1，2，3，4，5，6，下图是这个立方体表面的展开图，抛掷这个立方体，则朝上一面的数恰好等于朝下一面的数的的概率是（ ）
A． B．
C． D．
7．
四张完全相同的卡片上，分别画有圆、矩形、等边三角形、等腰梯形，现从中随机抽取一张，卡片上画的恰好是中心对称图形的概率为
（ ）
A．
B．
C．
D．
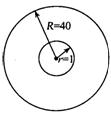
8． 如果小明将飞镖随意投中如图所示的图形木板，那么镖落在小圆内的概率为 （ ）
A． 
B．
C．
D．
二、填空题（每题4分，共24分）
1．“天有不测风云”这句话是说：世界上有很大事件具有偶数性，人们不能_______ _这些事情是否会发生．
2.如果一次试验中有：可能出现的结果有限多个；各种结果发生的可能性相等，则可用__ __求概率；当一次试验要涉及两个因素(例如掷两骰子)并且可能出现的结果数目较多时，为不重不漏地列出所有可能的结果，我们通常采用______ _求概率；当一次试验要涉及3个或3个以上的因素(例如从3个口袋中取球)时，列方形表就不方便了，为了不重不漏地列出所有可能结果，通常采用______ 求概率．
3．10张卡片分别写有0至9十个数字，将它们放入纸箱后，任意摸出一张，则P（摸到数字2）＝ ，P（摸到奇数）＝ 。
4．一只布袋中有三种小球（除颜色外没有任何区别），分别是2个红球，3个黄球和5个蓝球，每一次只摸出一只小球，观察后放回搅匀，在连续9次摸出的都是蓝球的情况下，第10次摸出黄球的概率是 。
5．掷两枚普通硬币，出现两个正面的概率是 。
6．小华与父母一同从南京乘火车到苏州乐园游玩，火车车厢里每排有左、中、右三个座位，小华一家三口随意坐某排的三个座位，则小华恰好坐在中间的概率是 。
7．小明和小颖按如下规则做游戏：桌面上放有5支铅笔，每次取1支或2支，由小明先取，最后取完铅笔的人获胜，如果小明获胜的概率为1，那么小明第一次应取走 支。
8．一副没有大小王的扑克，共52张，抽出一张是红桃的概率为 。
三、解答题（共44分）
15．（8分）一个口袋中有10个红球和若干个白球，请通过以下实验估计口袋中白球的个数，从口袋中随机摸出一球，记下其颜色，再把它放回口袋中，不断重复上述过程，实验中共摸200次，其中50次摸到红球。
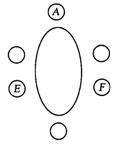16．（8分）一张椭圆形桌旁有六个座位，A、E、F先坐在如图所示的座位上，B、C、D三人随机坐到其他三个座位，求A与B不相邻而座的概率。
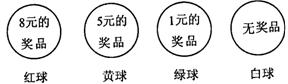
17．（10分）在摸奖活动中，游乐场在一只黑色的口袋里装有只颜色不同的50只小球，其中红球1只、黄球2只、绿球10只，其余为白球，搅拌均匀后，每2元摸1个球，奖品的标准在球上（如下图）。
(1) 如果花2元摸1个球，那么摸不到奖的概率是多少？
(2) 如果花4元同时摸2个球，那么获得10元奖品的概率是多少？
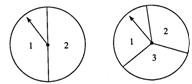18．（8分）小明和小刚用如图的两个转盘做游戏，游戏规则如下：分别旋转两个转盘，当两个转盘所转到的数字之积为奇数时，小明得2分；当所转到的数字之积为偶数时，小刚得1分，这个游戏对双方公平吗？若公平，说明理由；若不公平，如何修改规则才能使游戏双方公平？
19．（10分）两人去某风景区游玩，每天某一时段开往该风景区有三辆汽车，票价相同，但是他们不知道这些车的舒适程度，也不知道汽车开过来的顺序，两人采用了不同的乘车方案：
甲无论如何总是上开来的第一辆车，而乙则是先观察后上车，当第一辆车开来时，他不上车，而是仔细观察车的舒适状况，如果第二辆车的舒适程度比第一辆好，他就上第二辆车；如果第二辆车的舒适程度不比第一辆好，他就上第三辆车。如果把这三辆车的舒适程度分为上、中、下三等。请尝试着解决下面的问题：
(1) 三辆车按出现的先后顺序共有哪几种不同的可能？
(2) 你认为甲、乙采用的方案，哪一种方案使自己乘坐上等车的可能性大？为什么？