高级中等学校招生统一考试数学试卷(课标B卷)
| 考生须知 | 1.本试卷分为第Ⅰ卷、第Ⅱ卷,共10页,共九道大题,25个小题,满分120分.考试时间120分钟. 2.在试卷密封线内认真填写区(县)名称、毕业学校、姓名、报名号、准考证号. 3.考试结束,请将本试卷和答题卡一并交回. |
第Ⅰ卷(机读卷 共32分)
| 考生 须知 | 1.第Ⅰ卷共2页,共一道大题,8个小题. 2.试题答案一律填涂在机读答题卡上,在试卷上作答无效. |
一、选择题(共8个小题,每小题4分,共32分.)
下列各题均有四个选项,其中只有一个是符合题意的.用铅笔把“机读答题卡”上对应题目答案的相应字母处涂黑.
1.![]() 的相反数是( )
的相反数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.青藏高原是世界上海拔最高的高原,它的面积约为![]() 平方千米.将
平方千米.将![]() 用科学记数法表示应为( )
用科学记数法表示应为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.在函数![]() 中,自变量
中,自变量![]() 的取值范围是( )
的取值范围是( )
 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
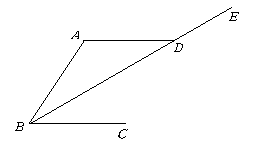
4.如图,![]() ,点
,点![]() 在
在![]() 的延长线上,
的延长线上,
若![]() ,则
,则![]() 的度数为( )
的度数为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5.小芸所在学习小组的同学们,响应“为祖国争光,为奥运添彩”的号召,主动到附近的7个社区帮助爷爷,奶奶们学习英语日常用语.他们记录的各社区参加其中一次活动的人数如下:33,32,32,31,28,26,32,那么这组数据的众数和中位数分别是( )
A.32,31 B.32,32 C.3,31 D.3,32
6.把代数式![]() 分解因式,结果正确的是( )
分解因式,结果正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
7.掷一枚质地均匀的正方体骰子,骰子的六个面上分别刻有1到6的点数,掷得面朝上的点数为奇数的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
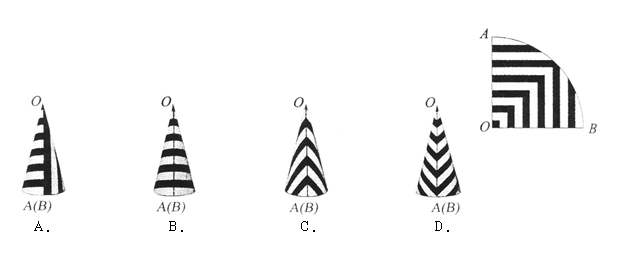 8.将如右图所示的圆心角为
8.将如右图所示的圆心角为![]() 的扇形纸片
的扇形纸片![]() 围成圆锥形纸帽,使扇形的两条半径
围成圆锥形纸帽,使扇形的两条半径![]() 与
与![]() 重合(接缝粘贴部分忽略不计),则围成的圆锥形纸帽是( )
重合(接缝粘贴部分忽略不计),则围成的圆锥形纸帽是( )
高级中等学校招生统一考试数学试卷(课标B卷)
第II卷(非机读卷 共88分)
| 考生 须知 | 1.第Ⅱ卷共8页,共八道大题,17个小题. 2.除画图可以用铅笔外,答题必须用黑色或蓝色钢笔、圆珠笔. |
二、填空题(共4个小题,每小题4分,共16分.)
9.若关于![]() 的一元二次方程
的一元二次方程![]() 有实数根,则
有实数根,则![]() 的取值范围是 .
的取值范围是 .
10.若![]() ,则
,则![]() 的值为 .
的值为 .
 11.用“
11.用“![]() ”定义新运算:对于任意实数
”定义新运算:对于任意实数![]() ,
,![]() ,都有
,都有![]()
![]() .例如,
.例如,![]()
![]() ,那么
,那么![]()
![]() ;
;
当![]() 为实数时,
为实数时,![]()
![]() .
.
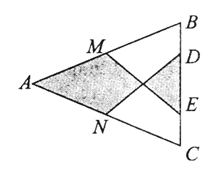
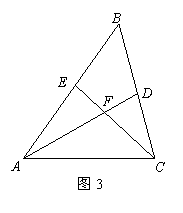
12.如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,![]() ,
,![]() 为
为![]() 上的点,连结
上的点,连结![]() ,
,![]() .若
.若![]() ,
,![]() ,
,![]() ,则图中阴影部分的面积为
,则图中阴影部分的面积为 ![]() .
.
三、解答题(共5个小题,共25分)
13.(本小题满分5分)
计算:![]() .
.
解:
14.(本小题满分5分)
解不等式组![]()
解:
15.(本小题满分5分)
解分式方程![]() .
.
解:
16.(本小题满分5分)
 已知:如图,
已知:如图,![]() ,点
,点![]() ,点
,点![]() 在
在![]() 上,
上,![]() ,
,![]() .
.
求证:![]() .
.
证明:
17.(本小题满分5分)
已知![]() ,求代数式
,求代数式![]() 的值.
的值.
解:
四、解答题(共2个小题,共11分.)
18.(本小题满分5分)
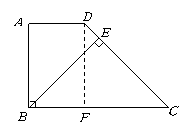
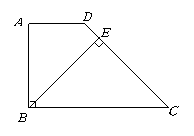 已知:如图,在梯形
已知:如图,在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 于点
于点![]() ,
,![]() ,
,![]() .
.
求:![]() 的长.
的长.
解:
19.(本小题满分6分)
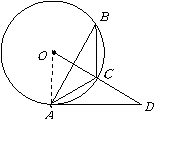
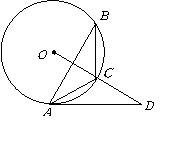 已知:如图,
已知:如图,![]() 内接于
内接于![]() ,点
,点![]() 在
在![]() 的延长线上,
的延长线上,![]() ,
,![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
(1)证明:
(2)解:
五、解答题(本题满分5分)
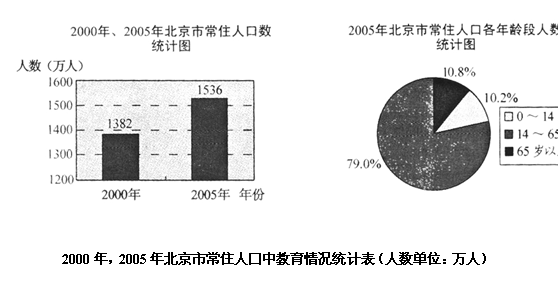 20.根据北京市统计局公布的2000年,2005年北京市常住人口相关数据,绘制统计图表如下:
20.根据北京市统计局公布的2000年,2005年北京市常住人口相关数据,绘制统计图表如下:
| 年份 | 大学程度人数(指大专及以上) | 高中程度人数(含中专) | 初中程度人数 | 小学程度人数 | 其他人数 |
| 2000年 | 233 | 320 | 475 | 234 | 120 |
| 2005年 | 362 | 372 | 476 | 212 | 114 |
请利用上述统计图表提供的信息回答下列问题:
(1)从2000年到2005年北京市常住人口增加了多少万人?
(2)2005年北京市常住人口中,少儿(![]() 岁)人口约为多少万人?
岁)人口约为多少万人?
(3)请结合2000年和2005年北京市常住人口受教育程度的状况,谈谈你的看法.
解:(1)
(2)
(3)
六、解答题(共2个小题,共9分.)
21.(本小题满分5分)
在平面直角坐标系![]() 中,直线
中,直线![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到直线
得到直线![]() .直线
.直线![]() 与反比例函数
与反比例函数![]() 的图象的一个交点为
的图象的一个交点为![]() ,试确定反比例函数的解析式.
,试确定反比例函数的解析式.
解:
22.(本小题满分4分)
请阅读下列材料:
问题:现有5个边长为1的正方形,排列形式如图1,请把它们分割后拼接成一个新的正方形.要求:画出分割线并在正方形网格图(图中每个小正方形的边长均为1)中用实线画出拼接成的新正方形.
小东同学的做法是:设新正方形的边长为![]() .依题意,割补前后图形的面积相等,有
.依题意,割补前后图形的面积相等,有![]() ,解得
,解得![]() .由此可知新正方形的边长等于两个正方形组
.由此可知新正方形的边长等于两个正方形组
成的矩形对角线的长.于是,画出如图2所示的分割线,拼出如图3所示的新正方形.
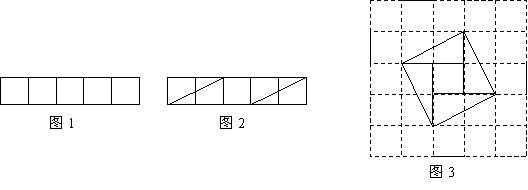 |
请你参考小东同学的做法,解决如下问题:
现有10个边长为1的正方形,排列形式如图4,请把它们分割后拼接成一个新的正方形.要求:在图4中画出分割线,并在图5的正方形网格图(图中每个小正方形的边长均为1)中用实线画出拼接成的新正方形.
 说明:直接画出图形,不要求写分析过程.
说明:直接画出图形,不要求写分析过程.
解:
七、解答题(本题满分6分)
23.如图1,![]() 是
是![]() 的平分线,请你利用该图形画一对以
的平分线,请你利用该图形画一对以![]() 所在直线为对称轴的全等三角形.
所在直线为对称轴的全等三角形.
请你参考这个作全等三角形的方法,解答下列问题:
(1)如图2,在![]() 中,
中,![]() 是直角,
是直角,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的平分线,
的平分线,![]() ,
,![]() 相交于点
相交于点![]() .请你判断并写出
.请你判断并写出![]() 与
与![]() 之间的数量关系;
之间的数量关系;
(2)如图3,在![]() 中,如果
中,如果![]() 不是直角,而(1)中的其他条件不变,
不是直角,而(1)中的其他条件不变,
请问,你在(1)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由.
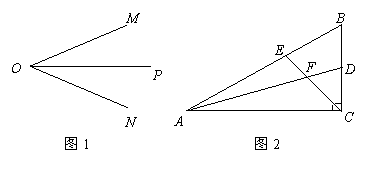 解:画图:
解:画图:
 |
(1)![]() 与
与![]() 之间的数量关系为 .
之间的数量关系为 .
(2)
八、解答题(本题满分8分)
24.已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点.
两点.
(1)求此抛物线的解析式;
 (2)若点
(2)若点![]() 为线段
为线段![]() 的一个三等分点,求直线
的一个三等分点,求直线![]() 的解析式;
的解析式;
(3)若一个动点![]() 自
自![]() 的中点
的中点![]() 出发,先到达
出发,先到达![]() 轴上的某点(设为点
轴上的某点(设为点![]() ),再到达抛物线的对称轴上某点(设为点
),再到达抛物线的对称轴上某点(设为点![]() ),最后运动到点
),最后运动到点![]() .求使点
.求使点![]() 运动的总路径最短的点
运动的总路径最短的点![]() ,点
,点![]() 的坐标,并求出这个最短总路径的长.
的坐标,并求出这个最短总路径的长.
解:(1)
(2)
(3)
九、解答题(本题满分8分)
25.我们给出如下定义:若一个四边形的两条对角线相等,则称这个四边形为等对角线四边形.请解答下列问题:
(1)写出你所学过的特殊四边形中是等对角线四边形的两种图形的名称;
(2)探究:当等对角线四边形中两条对角线所夹锐角为![]() 时,这对
时,这对![]() 角所对的两边之和与其中一条对角线的大小关系,并证明你的结论.
角所对的两边之和与其中一条对角线的大小关系,并证明你的结论.
解:(1)
(2)
高级中等学校招生统一考试数学试卷(课标B卷)
答案及评分参考
阅卷须知:
1.一律用红钢笔或红圆珠笔批阅,按要求签名.
2.第I卷是选择题,机读阅卷.
3.第II卷包括填空题和解答题.为了阅卷方便,解答题中的推导步骤写得较为详细,考生只要写明主要过程即可.若考生的解法与本解法不同,正确者可参照评分参考给分.解答右端所注分数,表示考生正确做到这一步应得的累加分数.
第I卷(机读卷 共32分)
一、选择题(共8个小题,每小题4分,共32分.)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答案 | A | C | A | D | B | C | D | B |
第II卷(非机读卷 共88分)
二、填空题(共4个小题,每小题4分,共16分.)
| 题号 | 9 | 10 | 11 | 12 | |
| 答案 |
| 2 | 10 | 26 | 30 |
三、解答题(本题共30分,每小题5分.)
13.解:![]()
![]() ························································································· 4分
························································································· 4分
![]() .···································································································· 5分
.···································································································· 5分
14.解:由不等式![]() 解得
解得 ![]() .························································ 2分
.························································ 2分
由不等式![]() 解得
解得 ![]() .····················································· 4分
.····················································· 4分
则不等式组的解集为 ![]() .····················································· 5分
.····················································· 5分
15.解:![]() .······················································· 2分
.······················································· 2分
![]() .···································································· 3分
.···································································· 3分
![]() .··········································································· 4分
.··········································································· 4分
经检验![]() 是原方程的解.
是原方程的解.
所以原方程的解是![]() .········································································ 5分
.········································································ 5分
16.证明:因为![]() ,
,
则![]() .····················································································· 1分
.····················································································· 1分
又![]() ,
,
则![]() .····················································································· 2分
.····················································································· 2分
在![]() 与
与![]() 中,
中,
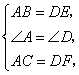 ·················································································· 3分
·················································································· 3分
所以![]() .···································································· 4分
.···································································· 4分
所以![]() .·················································································· 5分
.·················································································· 5分
17.解:![]()
![]() ··········································································· 2分
··········································································· 2分
![]() .····························································································· 3分
.····························································································· 3分
当![]() 时,原式
时,原式![]() .························· 5分
.························· 5分
四、解答题(共2个小题,共11分)
18.解:如图,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .············································· 1分
.············································· 1分
因为![]() ,
,
所以四边形![]() 是平行四边形.································································· 2分
是平行四边形.································································· 2分
 所以
所以![]() .
.
由![]() ,
,
得![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,
由![]() ,
,
求得![]() .································································································ 3分
.································································································ 3分
所以![]() .·············································································· 4分
.·············································································· 4分
在![]() 中,
中,![]() ,
,
![]() .
.
求得![]() .·························································································· 5分
.·························································································· 5分
19.解:(1)证明:如图,连结![]() .
.
 因为
因为![]() ,
,
所以![]() .
.
故![]() .································· 1分
.································· 1分
又![]() ,
,
所以![]() 是等边三角形.
是等边三角形.
故![]() .··························································································· 2分
.··························································································· 2分
因为![]() ,
,
所以![]() .
.
所以![]() 是
是![]() 的切线.················································································ 3分
的切线.················································································ 3分
(2)解:因为![]() ,
,
所以![]() 垂直平分
垂直平分![]() .
.
则![]() .·························································································· 4分
.·························································································· 4分
所以![]() .································································································ 5分
.································································································ 5分
在![]() 中,
中,![]() ,
,
由正切定义,有![]() .
.
所以![]() .··························································································· 6分
.··························································································· 6分
五、解答题(本题满分5分)
20.解:(1)![]() (万人).···························································· 1分
(万人).···························································· 1分
故从2000年到2005年北京市常住人口增加了154万人.
(2)![]() (万人).
(万人).
故2005年北京市常住人口中,少儿(![]() 岁)人口约为157万人.············· 3分
岁)人口约为157万人.············· 3分
(3)例如:依数据可得,2000年受大学教育的人口比例为![]() ,2005年受大学教育的人口比例为
,2005年受大学教育的人口比例为![]() .可知,受大学教育的人口比例明显增加,教育水平有所提高.·········································· 5分
.可知,受大学教育的人口比例明显增加,教育水平有所提高.·········································· 5分
六、解答题(共2个小题,共9分)
21.解:依题意得,直线![]() 的解析式为
的解析式为![]() .······················································· 2分
.······················································· 2分
因为![]() 在直线
在直线![]() 上,
上,
则![]() .································································································ 3分
.································································································ 3分
即![]() .
.
又因为![]() 在
在![]() 的图象上,
的图象上,
可求得![]() .························································································· 4分
.························································································· 4分
所以反比例函数的解析式为![]() .························································ 5分
.························································ 5分
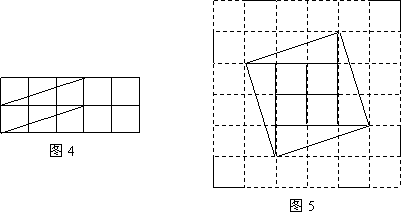 22.解:所画图形如图所示.
22.解:所画图形如图所示.
说明:图4与图5中所画图形正确各得2分.分割方法不唯一,正确者相应给分.
七、解答题(本题满分6分.)
23.解:图略.画图正确得1分.
(1)![]() 与
与![]() 之间的数量关系为
之间的数量关系为![]() .·············································· 2分
.·············································· 2分
(2)答:(1)中的结论![]() 仍然成立.
仍然成立.
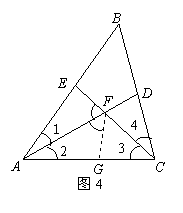 证法一:如图4,在
证法一:如图4,在![]() 上截取
上截取![]() ,连结
,连结![]() .·································· 3分
.·································· 3分
因为![]() ,
,![]() 为公共边,
为公共边,
可证![]() .
.
所以![]() ,
,![]() .···················· 4分
.···················· 4分
由![]() ,
,![]() 分别是
分别是![]() 的平分线,
的平分线,
可得![]() .
.
所以![]() .
.
所以![]() .······················································································· 5分
.······················································································· 5分
由![]() 及
及![]() 为公共边,可得
为公共边,可得![]() .
.
所以![]() .
.
所以![]() .····························································································· 6分
.····························································································· 6分
证法二:如图5,
过点![]() 分别作
分别作![]() 于点
于点![]() ,
,![]() 于点
于点![]() .································· 3分
.································· 3分
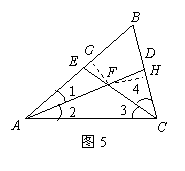 因为
因为![]() ,且
,且![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的平分线,
的平分线,
所以可得![]() ,
,![]() 是
是![]() 的内心.··············· 4分
的内心.··············· 4分
所以![]() ,
,![]() .
.
又因为![]() ,
,
所以![]() .····················································· 5分
.····················································· 5分
因此可证![]() .
.
所以![]() .····························································································· 6分
.····························································································· 6分
八、解答题(本题满分8分)
24.解:(1)根据题意,![]() ,
,
所以![]()
解得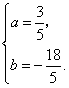
所以抛物线解析式为![]() .······················································ 2分
.······················································ 2分
(2)依题意可得![]() 的三等分点分别为
的三等分点分别为![]() ,
,![]() .
.
设直线![]() 的解析式为
的解析式为![]() .
.
当点![]() 的坐标为
的坐标为![]() 时,直线
时,直线![]() 的解析式为
的解析式为![]() ;························ 3分
;························ 3分
当点![]() 的坐标为
的坐标为![]() 时,直线
时,直线![]() 的解析式为
的解析式为![]() .······················ 4分
.······················ 4分
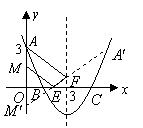 (3)如图,由题意,可得
(3)如图,由题意,可得![]() .
.
点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,
,
点![]() 关于抛物线对称轴
关于抛物线对称轴![]() 的对称点为
的对称点为![]() .
.
连结![]() .
.
根据轴对称性及两点间线段最短可知,![]() 的长就是所求点
的长就是所求点![]() 运动的最短总路径的长. 5分
运动的最短总路径的长. 5分
所以![]() 与
与![]() 轴的交点为所求
轴的交点为所求![]() 点,与直线
点,与直线![]() 的交点为所求
的交点为所求![]() 点.
点.
可求得直线![]() 的解析式为
的解析式为![]() .
.
可得![]() 点坐标为
点坐标为![]() ,
,![]() 点坐标为
点坐标为![]() .················································· 7分
.················································· 7分
由勾股定理可求出![]() .
.
所以点![]() 运动的最短总路径
运动的最短总路径![]() 的长为
的长为![]() .······························ 8分
.······························ 8分
九、解答题(本题满分8分)
25.解:(1)略.写对一种图形的名称给1分,最多给2分.
(2)结论:等对角线四边形中两条对角线所夹锐角为![]() 时,这对
时,这对![]() 角所对的两边之和大于或等于一条对角线的长.······················································································································· 3分
角所对的两边之和大于或等于一条对角线的长.······················································································································· 3分
已知:四边形![]() 中,对角线
中,对角线![]() ,
,![]() 交于点
交于点![]() ,
,![]() ,
,
且![]() .
.
求证:![]() .
.
证明:过点![]() 作
作![]() ,在
,在![]() 上截取
上截取![]() ,使
,使![]() .
.
连结![]() ,
,![]() .····························································································· 4分
.····························································································· 4分
故![]() ,四边形
,四边形![]() 是平行四边形.
是平行四边形.
所以![]() 是等边三角形,
是等边三角形,![]() .······················································· 6分
.······················································· 6分
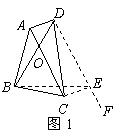 所以
所以![]() .
.
①当![]() 与
与![]() 不在同一条直线上时(如图1),
不在同一条直线上时(如图1),
在![]() 中,有
中,有![]() .
.
所以![]() .······················································· 7分
.······················································· 7分
②当![]() 与
与![]() 在同一条直线上时(如图2),
在同一条直线上时(如图2),
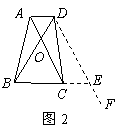 则
则![]() .
.
因此![]() .······················································· 8分
.······················································· 8分
综合①、②,得![]() .
.
即等对角线四边形中两条对角线所夹角为![]() 时,这对
时,这对![]() 角所对的两边之和大于或等于其中一条对角线的长.
角所对的两边之和大于或等于其中一条对角线的长.