高级中等学校招生学业考试数学试卷
（时间100分钟，满分120分）
一、选择题（每小题3分，共18分）
下列各小题均有四个答案，其中只有一个是正确的，将正确答案的代号字母填入题后括号内
1．-
的倒数是
[ ]
A．-3
B.3
C.-
D.
2. 2005年末我国外汇储备达到8189亿美元,8189亿用科学记数法表示(保留3个有效数
字) 是 [ ]
A.8.19×10
B.8.18×10
C.8.19×10
D.8.18×10
3.在一个不透明的布袋中,红色、黑色、白色的玻璃球共有40个,除颜色外其它完全相同.
小李通过多次摸球试验后发现其中摸到红色、黑色 球的频率稳定在15℅和45℅，则口袋中
白球的个数很可能是 [ ]
A.6 B.16 C.18 D.24
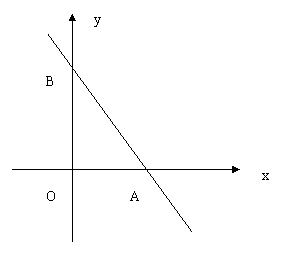
4.如图,一次函数y=kx+b的图象经过A\B两点,则kx+b0的解集是 [ ]
A.x﹥0 B.x﹥2
|
|
C. x﹥-3 D. -3 ﹤x﹤2
5.由一些大小相同的小正方体组成的几何体的三视图如图所示,那么,组成这个几何体的小正方体体有 [ ]
A.10∏cm B.10cm C.15∏cm D.20∏cm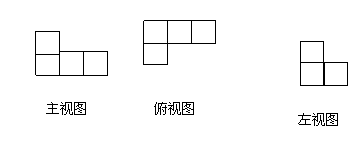 
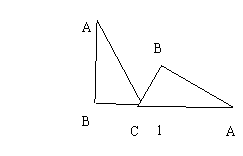
6．如图，一块含有30
角的直角三角形ABC，在水平桌面上绕点C按顺时针方向旋转到A
B
C的位置.若BC的长为15cm,那么顶点A从开始到结束所经过的路径长为
[ ]
A.10∏cm B.10∏cm C.15∏cm D.20∏cm
二、填空题（每小题3分，共27分）
7、函数y=
中，自变量x的取值范围是------------------
8、写出一个图象位于第二、四象限的反比例函数的表达式--------------------
9、在“手拉手活动”中，小明为捐助某贫困山区的一名同学，现已存款300元，他计划今后每月存款10元，n个月后存款总数是元--------------
10、如图，点A、B、C是⊙0上的三点，若∠BOC=56，则∠A的度数为-----------------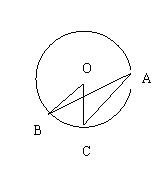
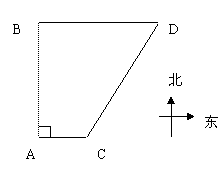
11、如图，C、D是两个村庄，分别位于一个湖的南、北两端A和B的正东方向上，且D位于C的北偏东30方向上，CD=6cm，则AB=cm--------------------------
12、已知二次函数y=-x
+2x+c的对称轴和x轴相交于点（m，0），则m的值为-------------------
13、要拼出和图1的菱形相似的较长对角线为88cm的大菱形（如图2所示），需要图1中的菱形的个数为------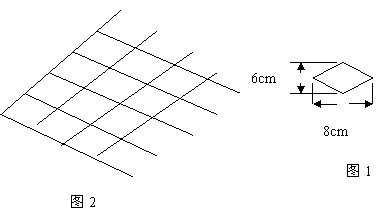 
14、如图，在ABC中，AC=BC=2，∠ACB=90，D是BC边的中点，E是AB边上一动点，则EC+ED的最小值是--------------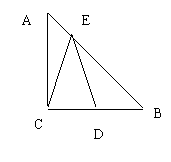
15．如图，把矩形纸片OABC放入平面直角坐标系中，使OA、OA分别落在x轴、y轴上，连结OB，将纸片OABC沿OB折叠，使点A落在点A
的位置，若OB=
，tan∠BOC=
，则点A的坐标为------------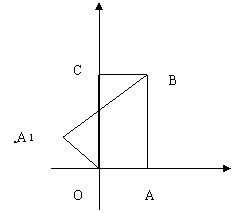
三、解答题（本大题共8个小题，满分75分）
16．（8分）计算：
（2－
）
．（2+）
－2cos30－（－
）
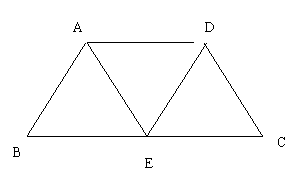
17如图，梯形ABCD中，AD∥BC，AB=AD=DC，E为底边BC的中点，且DE∥AB.试判断△ADE的形状,并给出证明
.
18.(9分)一枚均匀的正方体子,六个面分别标有1,2,3,4,5,6,连续抛掷两次,朝上的数字分别是m,n,若把m,n作为点A的横、纵坐标，那么点A（m，n）在函数y=2x的图象上的概率是多少？
19．（9分）某公司员工的月工资情况统计如下表：
| 员工人数 | 2 | 4 | 8 | 20 | 8 | 4 |
| 月工资（元） | 5000 | 4000 | 2000 | 1500 | 1000 | 700 |
（1） 分别计算该公司员工月工资的平均数、中位数和众数；
（2） 你认为用（1）中计算出的哪个数据来代表该公司员工的月工资水平更为合适？请简要说明理由；
（3） 请画出一种你认为合适的统计图来表示上面表格中的数据.
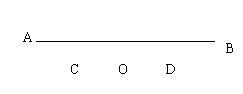
20.(9分)如图,线段AB=4,点O是线段AB上一点,C、D分别是线段OA、OB的中点，小明据此很轻松地求得CD=2。他在反思过程中突发奇想：若点O运动到AB的延长线上或点O在AB所在的直线外，原有的结论“CD=2”是否仍然成立？请帮小明画出图形并说明理由。
21．（10分）甲、乙两家超市以相同的价格出售同样的商品，为了吸引顾客，各自推出不同的优惠方案：在甲超市累计购买商品超出300元之后，超出部分按原价8折优惠；在乙超市累计购买商品超出200元之后，超出部分按原价8.5折优惠.设顾客预计累计购物x元(300).
(1)请用含的代数式分别表示顾客在两家超市购物所付的费用;
(2)试比较顾客到哪家超市购物更优惠?说明理由.
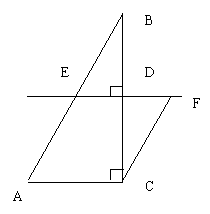
22.(10分)如图,在ABC中,∠ACB=90,AC=2,BC=3.D是BC边上一点,直线DE⊥BC于D,交AB于E,CF∥AB交直线DE于F.设CD=.x
(1)当x取何值时,四边形EACF是菱形?请说明理由;
(2)当x取何值时,四边形EACD的面积等于2?
23.(11分)如图,在平面直角坐标系中,直线y=-
x+4分别交x轴、y轴于A、B两点
（1）求A、B两点的坐标；
（2）设P是直线AB上一动点（点P不与点A重合），⊙P始终和x轴相切，和直线AB相交于C、D两点（点C的横坐标小于点D的横坐标）.设P点的横坐标为m，试用含有m的代数式表示C点的横坐标；
（3）在（2）的条件下，若点C在线段AB上，求m为何值时，△BOC为等腰三角形.
