九年级第三次联考数学测试
一、选择题【3分×10=30分】
1.下列函数中,属于二次函数的是 ( )
A.
B.
C.
D.
2.下列命题：①长度相等的弧是等弧 ②半圆既包括圆弧又包括直径 ③相等的圆心角所对的弦相等 ④外心在三角形的一条边上的三角形是直角三角形,正确的命题共有 （ ）
A．0个 B．1个 C．2个 D．3个
3.抛物线y=（x+3）2-2的对称轴是 ( )
A.直线x=3 B.直线x=－3 C.直线x=－2 D.直线x=2
4.若数据2,x,4,8的平均数是4,则这组数据的极差和方差分别是 ( )
A.6和6 B.6和16 C.4和24 D.4和 16
5.某商品连续两次降价10%后的价格为a元，该商品的原价为 （ ）
A. 元 B．1.12a元 C．元 D．0.92a元
6.下列运算式正确的个数是 ( )
A.1个 B.2个 C.3个 D.4个
7.若PA与PB切⊙O于点A、B,点C是圆上的点（不与点A、B重合），若
∠P=68 °，则∠ ACB的度数 ( )
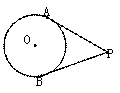A. 56 ° B. 124° C.56 °或124 ° D. 112 °
第7题图 第8题图
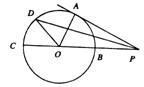
8.如图所示，PA切⊙O于点A，线段PBC经过圆心O交圆于B、C两点，OB=PB=1，OA绕点O逆时针方向旋转60°到OD，则PD的长为 （ ）
A. B. C. D. 2
9.给出下列函数：(1)y=2x;
(2)y=-2x+1; (3)y=
(x>0) (4)y=x2(x<-1)
其中，y随x的增大而减小的函数是 ( )
A.(1)(2) B.(1)(3) C.(2)(4) D.(2)(3)(4)
10.设⊙O的半径为2，圆心O到直线l的距离OP＝m，且m使得关于x的方程
有实数根，则直线l与⊙O的位置关系为 （ ）
A.相离或相切 B.相切或相交 C.相离或相交 D.无法确定
二、填空题【3分×8=24分】
11.抛物线 y=
的开口向
.
12.Rt△ABC的斜边是AB，它的外接圆面积是121π平方厘米，则AB= .
13.抛物线是
由抛物线
先向沿y轴向 平移 个单位,再沿x轴向 平移 个单位得到的.
14.抛物线y=mx2-6x+1与x轴有交点，则m的取值范围为 .
15.二次函数y=ax2+bx+c,当x=1.5时,y<0;当x=1.25时,y>0;当x=1.35时,y<0.则点A的横坐标约是 (精确到0.1).
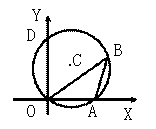
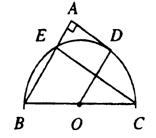16.如图,⊙C过原点,并与两坐标轴分别交于A、D两点,已知∠OBA=30°,点D的坐标为(0,2),则点A的坐标为
,圆心C的坐标为
.
第17题图 第18题图 第16题图
17.如图，两个半圆中，长为6的弦CD与直径AB平行且与小半圆相切，那么图中阴影部分的面积等于_____ .
18.如图所示，BC为半圆O的直径，点D是半圆上一点，过点D作⊙O的切线AD、BA⊥DA于A，BA交半圆于E，已知BC=10，AD=4，那么直线CE与以点O为圆心，为半径的圆的位置关系是 。
三、解答题
19.【6分】
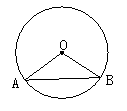
20.【6分】如图,在⊙O中,半径OA=4,弦AB=4
,用扇形OAB做一个圆锥的侧面,求这个圆锥的表面积.
 |
21.【6分】用配方法证明代数式2x2-x+3的值不小于
22.【8分】已知关于x的一元二次方程（1-2k）x2-2x-1=0有两个不相等的实数根，求k的取值范围.
23.【8分】已知:二次函数
求证:不论a取何值时,抛物线
与x轴都有两个不同的交点.
24．【8分】如图，在△ABC中，以AB为直径的⊙O交BC于点D，连结AD，（1）请你填加一个条件，使△ABD≌△ACD，并说明全等的理由．
你填加的条件是： ．
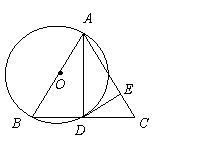（2）在（1）的基础上，过点D作DE⊥AC，垂足为E，此时，判断DE是否为⊙O的切线，并请你说明理由．
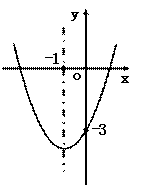
25.【10分】二次函数y=x2+bx+c的图象如图所示.
(1)求此二次函数的解析式;
(2)当x满足什么条件时,函数值y<0.
(3)把此抛物线向上平移多少个单位时,抛物线与x轴有两个交点?并写出平移后的抛物线的解析式.
26.【10分】西瓜经营户以2元/千克的价格购进一批小型西瓜，以3元/千克的价格出售，每天可售出200千克。为了促销,该经营户决定降价销售。经调查发现，这种小型西瓜每降价O.1元/千克，每天可多售出40千克。另外，每天的房租等固定成本共24元。该经营户要想每天盈利2O0元，应将每千克小型西瓜的售价降低多少元?
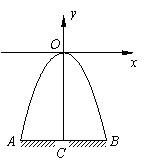
27．【10分】如图，某隧道口的横截面是抛物线形，已知路宽AB为6米，最高点离地面的距离OC为5米．以最高点O为坐标原点，抛物线的对称轴为y轴，1米为数轴的单位长度，建立平面直角坐标系，求:（1）以这一部分抛物线为图象的函数解析式，并写出x的取值范围；（2）有一辆宽2.8米，高1米的农用货车（货物最高处与地面AB的距离）能否通过此隧道？
 |
28.【12分】如图1，直线
与
x 轴相交于点A，与 y 轴相交于点B，点C(m，n)是第二象限内任意一点，以点C为圆心的圆与 x 轴相切于点E，与直线AB相切于点F.
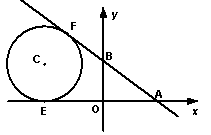⑴当四边形OBCE是矩形时，求点C的坐标；
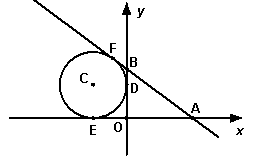
⑵如图2，若⊙C与 y 轴相切于点D，求⊙C的半径r；
⑶求m与n之间的函数关系式；
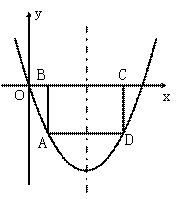
29.【12分】如图,点A是抛物线y=x2-3x上位于x轴下方,且在对称轴左侧的一个动点,过A点作x轴的平行线,交抛物线于另一点D,再作AB⊥x轴于点B,DC⊥x轴于点C.
(1)当BC=1时,矩形ABCD的周长= ;
(2)若设A点的横坐标为m.
①AB的长= .(用含m的代数式表示);
②试问矩形ABCD的周长是否存在最大值?若存在,请求出这个最大值,并指出此时点A的坐标;如果不存在,请说明理由.
