初中毕业暨高中阶段招生数学试题
注意事项：
1． 考试时间120分钟，全卷总分120分．
2． 答题前将密封线内的项目填写清楚．
3． 答卷一律使用黑、蓝钢笔或圆珠笔．
4． 凡使用答题卡的考生，答卷前务必将答题卡上的有关项目涂写清楚．选择题的每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案．不使用答题卡的考生，将选择题的答案答在试卷上．
一、选择题（下列每小题所给的四个答案中只有一个是正确的，每小题3分，共24分）
1．下列计算正确的是（ ）
Ａ．
Ｂ．
Ｃ．
Ｄ．
2．把多项式
分解因式的结果是（ ）
Ａ．
Ｂ．
Ｃ．
Ｄ．
3．右图是甲、乙两组数据的折线统计图，下列结论中正确的是（ ）
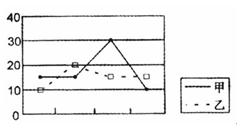Ａ．甲组数据比乙组数据稳定
Ｂ．乙组数据比甲组数据稳定
Ｃ．甲、乙两组数据一样稳定
Ｄ．不能比较两组数据的稳定性
4．若
三点都在函数
的图象上，则
的大小关系是（ ）
Ａ．
Ｂ．
Ｃ．
Ｄ．
5．某城市计划经过两年的时间，将城市绿地面积从今年的144万平方米提高到225万平方米，则每年平均增长（ ）
Ａ．
Ｂ．
Ｃ．
Ｄ．
6．如图，以
的直角边
所在的直线为轴，将
旋转一周，所形成的几何体的俯视图是（ ）
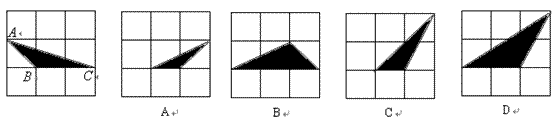
7．如图，每个大正方形均由边长为1的小正方形组成，则下列图中的三角形（阴影部分）与相似的是（ ）
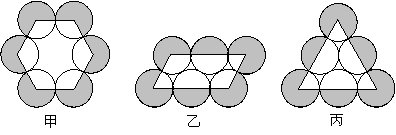
8．如图，有六个等圆按甲、乙、丙三种摆放，使相邻两圆互相外切，圆心连线分别构成正六边形、平行四边形、正三角形．圆心连线外侧的六个扇形（阴影部分）的面积之和依次记为
，则（ ）
Ａ．
Ｂ．
Ｃ．
Ｄ．
二、填空题（每小题3分，共24分）
9．计算：
．
10．如图，
，
分别交
于
，
，垂足为
，若
，则
的度数为
．
11．菱形的周长为20cm，一条对角线长为8cm，则菱形的面积为 
．
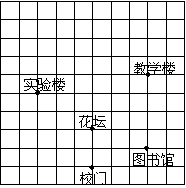
12．右图是某学校的平面示意图，在
的正方形网
格中（每个小方格都是边长为1的正方形），如果分别
用
表示图中图书馆和教学楼的位置，那么实
验楼的位置应表示为 ．
13．等腰梯形
中，
，
，
，则等腰梯形的周长是
cm．
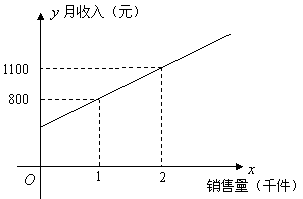
14．某公司销售人员的个人月收入与其每月的销售
量成一次函数关系，图象如图所示，则此销售人员
的销售量为3千件时的月收入是 元．
15．圆锥的侧面展开图的面积是
，母线长
为5cm，则圆锥的底面半径长为 cm．
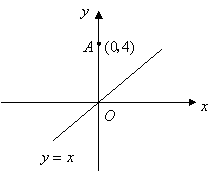16．如图，
的圆心坐标为
，若的半径为3，则直线
与的位置关系是 ．
三、解答题（共24分）
17．（6分）解不等式
，并把解集表示在数轴上．
18．（6分）已知
，求代数式
的值．
19．（6分）已知
满足方程组
，求代数式
的值．
20．（6分）
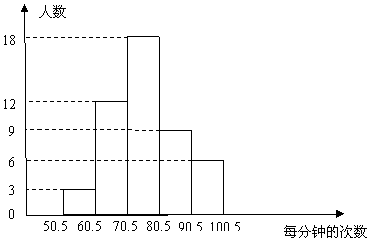
某中学将踢踺子作为趣味运动会的一个比赛项目，九年级（2）班同学进行了选拔测试，将所测成绩进行整理，分成五组，并绘制成频数分布直方图（如图所示）．请结合直方图提供的信息，回答下列问题：
（1）该班共有 名学生参加这次测试；
（2）60.5～70.5这一分数段的频数为 ，频率为 ；
（3）这次测试成绩的中位数落在 分数段内；
四、解答题（共48分）
21．（6分）
如图，点
在圆上，弦
的延长线与弦
的延长线相交于点
．
给出下列三个条件：
①
是圆的直径；
②
是
的中点；
③
．
请在上述条件中选取两个作为已知条件，第三个作为结论，写出一个你认为正确的命题，并加以证明．
条件： ．
结论： ．
证明：
22．（6分）
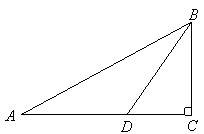如图，在中，
，
，是
平分线，
．求的长．
23．（8分）
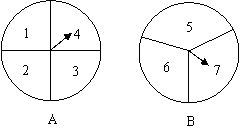
如图，有两个质地均匀的转盘
，转盘
被四等分，分别标有数字
；转盘
被3等分，分别标有数字
．小强与小华用这两个转盘玩游戏，小强说：“随机转动转盘各一次，转盘停止后，将转盘的指针所指的数字相乘，积为偶数我赢；积为奇数你赢．”
（1）小强指定的游戏规则公平吗？通过计算说明理由．
（2）请你只在转盘上修改其中一个数字，使游戏公平．
24．（8分）
在边长为6cm的正方形中，点
分别按
的方向同时出发，以1cm/s的速度匀速运动．
（1）在运动中，点所形成的四边形
为（ ）
Ａ．平行四边形 Ｂ．矩形
Ｃ．菱形 Ｄ．正方形
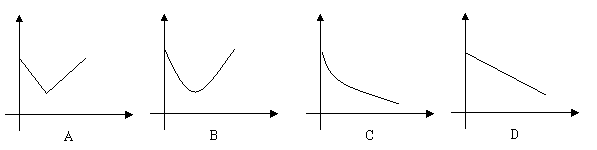（2）四边形的面积
随运动时间
变化的图象大致是（ ）
（3）写出四边形的面积
关于运动时间变化的函数关系式，并求运动几秒钟时，面积最小？最小值是多少？
25．（10分）
为了提高土地的利用率，将小麦、玉米、黄豆三种农作物套种在一起，俗称“三种三收”，这样种植的方法可将土地每亩的总产量提高
．
下表是这三种农作物的亩产量、销售单价及种植成本的对应表：
| 小麦 | 玉米 | 黄豆 | |
| 亩产量（千克） | 400 | 680 | 250 |
| 销售单价（元／千克） | 2 | 1 | 2.6 |
| 种植成本（元／亩） | 200 | 130 | 50 |
现将面积为10亩的一块农田进行“三种三收”套种，为保证主要农作物的种植比例，要求小麦的种植面积占整个种植面积的一半．
（1）设玉米的种植面积为
亩，三种农作物的总销售价为
元，写出与的函数关系式；
（2）在保证小麦种植面积不变的情况下，玉米、黄豆的种植面积均不得低于一亩，且两种农作物均以整亩数种植，三种农作物套种的种植亩数，有哪几种种植方案？
（3）在（2）中的种植方案中，采用哪种套种方案，才能使总销售价最高？最高价是多少？
（4）在（2）中的种植方案中，采用哪种套种方案，才能使总利润最大？最大利润是多少？（总利润＝总销售价－总成本）．
26．（10分）
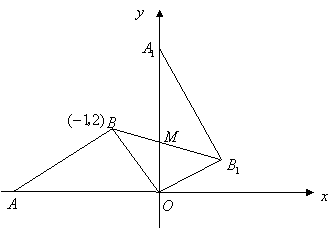
如图，在平面直角坐标系中，点在轴上，
是直角三角形，
，点的坐标为
．将绕原点
顺时针旋转
得到
．
（1）在旋转过程中，点所经过的路径长是多少？
（2）分别求出点
的坐标；
（3）连接
交
于点
，求
的值．