上余初中2006年上学期期中试卷
初三数学 命题人:姜桂英
校名: 班名: 姓名: 得分:
一、选择题(本题共12题,每小题4分,共48分)
1、下列运算正确的是( )
A、a2·a3=a6 B、a3÷a=a3 C、(a2)3=a5 D、2a-2=
2、地球的质量为6×1013亿吨,太阳的质量是地球质量的3.3×105倍,太阳的质量用科学记数法表示为( )吨。
A、1.98×1026 B、1.98×1027 C、1.98×1028 D、1.98×1063
3、二次函数y=x2+bx+c的图像上有两点(3,-8)和(-5,-8),则此抛物线的对称轴是直线( )
A、x=4 B、x=3 C、x=-5 D、x=-1
4、∠A、∠B、∠C为锐角△ABC的三个内角,且满足条件+ tanB- =0,
AB=4,则△ABC的面积等于( )
A、4 B、2 C、2 D、4
5、一块直径为20cm半圆形的铁皮做成一个圆锥漏斗,则漏斗口的直径是( )
A、5cm B、5cm C、10cm D、10cm
6、在一个不透明的口袋中装有若干个只有颜色不同的球,如果口袋中装有4个红球,且摸出红球的概率为,那么袋中共有球的个数为( )
A、12 B、9 C、7 D、6
7、如图(1),PA切⊙O于A点,PO交⊙O于E,PE=4,则PO的值是( )
A、16 B、14 C、12 D、10
8、已知一次函数y=kx+b的图像(如图2),当x<0时,y的取值范围是( )
A、y>0 B、y<0 C、-2<y<0 D、y<-2
9、如图3,在一个规格为4×8的球台上,有两个小球P和Q,若击打小球P经球台的边AB反弹后恰好击中小球Q,则小球P击出时,应瞄准AB边上的( ) 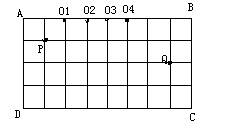
A、O1 B、O2 C、O3 D、O4
10、下图是甲、乙两户居民家庭全年支出费用的扇形统计图,根据统计图,下面对全年食品支出费用判断正确的是( )
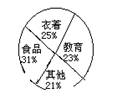
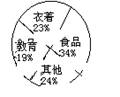
A、甲户比乙户多 B、乙户比甲户多 C、甲乙两户一样多 D、无法确定
11、如图5,立方体面上的AB1和AC间的夹角度数是( )
A、600 B、450 C、900 D、300
12、已知,如图6⊙Ο1与⊙Ο2外切于C点,AB是一条外公切线,A、B分别为切点,连AC、BC,设⊙Ο1的半径为R,⊙Ο2的半径为r,若tan∠ABC=( )
A、 B、 C、2 D、3
二、填空题
13.如图7,已知方格纸中是4个相同的正方形,则∠1+∠2+∠3=_______
14.某商品的进价400元,标价550元,按标价的8折出售,该商品的利润率是_______
15.学校食堂出售两种厚度一样但大小不同的面饼,小饼直径30cm,售价30分,大饼直径40cm,售价40分,你更愿意买_______饼,原因是______
16.如图8,如果ΔAPB绕点B按逆时针方向旋转300后,得到ΔA,P,B,且BP=2,那么PP,的长为_______(不取近似值,以下数据供解题使用:sin150=
17.在如图9的方格纸上,每小格都是边长为1的正方形,点A、B是方格纸中的两个格点(即正方形的顶点),在这个5×5的方格纸中找出格点C,使ΔABC的面积为2个平方单位,则满足条件的格点C的个数是_______
18.如图10,张敏同学的狼狗“赛赛”的狗窝是边长为2的正方形,用长为3m的皮带将狗拴在A点,在狗窝外面狗所能活动的范围为_______m2
三.解答题(共72分)
19.每小题4分,共8分
(1)、计算:-1+50-·sin450+2-1
(2)、化简:
20.(8分)
如图11所示,AB、AC分别是☉O的直径和弦,D为劣弧AC⌒上一点,DE^AB于点H,交⊙O于点E,交AC于点F,P为ED延长线上一点,
(1)、当△PCF满足什么条件时,PC与⊙O相切,为什么?
(2)、当点D在劣弧AC的什么位置时,才能使AD2=DE·DF?
21、某种洗衣机在洗涤衣服时,经历了进水清洗,排水,脱水四个连续的过程,其中进水,清洗,排水时洗衣机中的水量y(升)与时间x(分钟)之间关系如折线图12所示,根据图象,解答下列问题
(1)、洗衣机的进水时间是多少分钟?清洗时洗衣机中的水量是多少升?
(2)、已知洗衣机的排水速度为每分钟19升
① 求排水时y与x之间的关系式
② 如果排水时间为2分钟,求排水结束时,洗衣机中剩下的水量
22、(9分):
在数学活动课上,老师要求同学们先做下面的“循环分割”操作,然后再探索规律.图1是一张等腰梯形纸片,其腰长与上底长相等,且底角分别为600和1200,按要求开始操作(每次分割,纸片均不得留有剩余)
第1次分割:先将原等腰梯形纸片分割成3个全等的正三角形,然后将分割出的一个正三角形分割成3个全等的等腰梯形。
第2次分割:先将上次分割出的3个等腰梯形中的一个分割成3个全等的正三角形,然后将刚分割出的一个正三角形分割成3个全等的等腰三角形。
以后按第2次分割的方法进行下去
(1)、请你在图2中画出第一次分割的方案图。
(2)、若原等腰梯形的面积为a,请你通过操作,观察,将第2次,第3次分割后所得的一个最小等腰梯形面积分别填入下表:
| 分割次数(几) | 1 | 2 | 3 | …… |
| 一个最小等腰梯形面积(s) |
|
(3),请你猜想,分割所得的一个最小等腰梯形面积S与分割次数n有何关系?(请直接用含a的式子表示,不需写推理过程。)
23.如图,在正方形AOBC中,点C的坐标为(4,0),动点P,Q同时从O出发,P沿OACB的方向以每秒1个单位长的速度运动,Q沿OBCA方向以每秒2个单位长的速度运动,运动到相遇时停止,设S△OPQ=y,运动时间为t,
(1)P.Q何时相遇?相遇在哪一条边上?
(2)求y与t的函数关系式
(3)通过作图,判断t为何值时,y有最大值
24、已知:如图所示,P、A、B是x轴上的三点,点A的坐标为(-1,0),点B的坐标为(3,0),且PA:AB=1:2,以AB为直径画⊙M交y轴正半轴于点C
(1)、求证:PC是⊙M的切线
(2)、在x轴上是否存在这样的点Q,使得直线QC与过A、C、B三点的抛物线只有一个交点,若存在求点Q的坐标,若不存在,请说明理由
(3)、画⊙N,使得圆心N在x轴的负关轴上,⊙N与⊙M外切,且与直线PC相切于D,问将过A、C、B三点的抛物线平移后能否同时经过P、D、A三点?为什么?
![]()
![]()
![]()