初中毕业生学业仿真考试数学试卷
数 学
真情提示:亲爱的同学,欢迎你参加本次考试,祝你答题成功!
本试题共有24道题.其中1-10题为选择题,请将所选答案的标号填写题后面给出的括号上;11-16题为填空题,请将做出的答案填写在题后面给出的空格上;17-24题,请在试卷上给出的本题位置上做答.
一.选择题(本大题共10个小题,每小题4分,共40分)
1.下列计算正确的是 ———————————————————( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
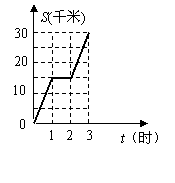 2.如图是某人骑自行车的行驶路程
2.如图是某人骑自行车的行驶路程![]() (千米)与行驶 时间
(千米)与行驶 时间![]() (时)的函数图象,下列说法不正确的是( )
(时)的函数图象,下列说法不正确的是( )
A.从0时到3时,行驶了30千米
B.从1时到2时匀速前进
C.从1时到2时在原地不动
D.从0时到1时与从2时到3时的行驶速度相同
3.圆的半径分别为3cm和4cm,圆心距为5cm,则两圆的位置关系为————————————( )
(A)内切 (B)外切 (C)外离 (D)相交
4.在平面直角坐标系中,![]() 三点的坐标分别为(0,0)、
三点的坐标分别为(0,0)、![]() 、
、![]() ,以这三点为平行四边形三的三个顶点,则第四个顶点不可能在————————————————————————————( )
,以这三点为平行四边形三的三个顶点,则第四个顶点不可能在————————————————————————————( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
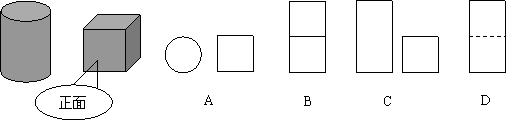
5.小明从正面观察下图所示的两个物体,看到的是( ).
6.抛物线![]() 的对称轴是————————————( )
的对称轴是————————————( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
7.如果不等式![]() 的正整数解是1,2,3,那么实数
的正整数解是1,2,3,那么实数![]() 的取值范围是——————————————————————————( )
的取值范围是——————————————————————————( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.下列四个生活、生产现象:①用两个钉子就可以把木条固定在墙上;②植树时,只要定出两棵树的位置,就能确定同一行树所在的直线;③从![]() 地到
地到![]() 地架设电线,总是尽可能沿着线段
地架设电线,总是尽可能沿着线段![]() 架设;④把弯曲的公路改直,就能缩短路程,其中可用公理“两点之间,线段最短”来解释的现象有( )
架设;④把弯曲的公路改直,就能缩短路程,其中可用公理“两点之间,线段最短”来解释的现象有( )
A.①② B.①③ C.②④ D.③④
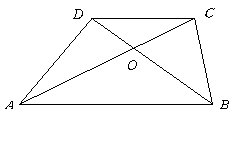
9.如图,梯形![]() 中,
中,![]() ,对角线
,对角线![]() 相交于
相交于![]() ,下面四个结论:
,下面四个结论:
 ①
①![]() ②
②![]()
③![]() ;④
;④![]() .
.
其中结论始终正确的有——————( )
A.1个 B.2个
C.3个 D.4个
10.如右图,在![]() 中,
中,![]() ,
,
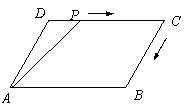 点
点![]() 从起点
从起点![]() 出发,沿
出发,沿![]() 向终点
向终点![]() 匀运动.设点
匀运动.设点![]() 所走过的路程为
所走过的路程为![]() ,点
,点![]() 所经过的线段与线段
所经过的线段与线段![]() 所围成图形的面积为
所围成图形的面积为![]() ,
,![]() 随
随![]() 的变化而变化.在下列图象中,能正确反映
的变化而变化.在下列图象中,能正确反映![]() 与
与![]() 的函数关系的是
的函数关系的是
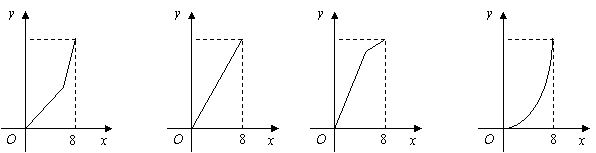 ————————————————————————————( )
————————————————————————————( )

二.填空题(每小题5分,共30分)
12.不等式组![]() 的解集为 .
的解集为 .
13.某学校的平面示意图如图所示,如果实验楼所在位置的坐标为![]() ,教学楼所在位置的坐标为
,教学楼所在位置的坐标为![]() ,那么图书馆所在位置的坐标为
.
,那么图书馆所在位置的坐标为
.
 14.如图,将矩形
14.如图,将矩形![]() 沿直线
沿直线![]() 折叠,顶点
折叠,顶点![]() 恰好落在
恰好落在![]() 边上
边上![]() 点处,已知
点处,已知![]() cm,
cm,![]() cm.则图中阴影部分面积为 cm
cm.则图中阴影部分面积为 cm![]() .
.
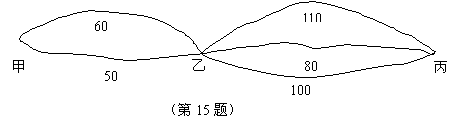
15.五一”黄金周期间,梁先生驾驶汽车从甲地经过乙地到丙地游玩.甲地到乙地有2条公路,乙地到丙地有3条公路.每一条公路的长度如下图所示(单位:km).梁先生任选一条从甲地到丙地的路线,这条路线正好是最短路线的概率是 .
16.已知一次函数![]() (
(![]() 、
、![]() 是常数),
是常数),![]() 与
与![]() 的部分对应值如下表:
的部分对应值如下表:
|
|
|
| 0 | 1 | 2 | 3 |
|
| 6 | 4 | 2 | 0 |
|
|
那么方程![]() 的解是 ;不等式
的解是 ;不等式![]() 的解集是 .
的解集是 .
三.解答题(本大题共8个小题;共80分.解答应写出文字说明、证明过程或演算步骤)
17.(本题满分8分.每小题4分)
(1)计算:![]() .
.
 (2)先化简后求值:
(2)先化简后求值:![]() ,其中
,其中![]()
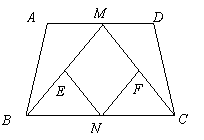
18.(本题满分8分)如图,等腰梯形![]() 中,
中,![]() .
.![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,
的中点,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点.
的中点.
(1)
求证:四边形![]() 是菱形;
是菱形;
(2)
若四边形![]() 是正方形,请探索等腰梯形
是正方形,请探索等腰梯形![]() 的高和底边
的高和底边![]() 的数量关系,并证明你的结论.
的数量关系,并证明你的结论.
19.(本小题满分8分)在“五一黄金周”期间,小明和他的父母坐游船从甲地到乙地观光,在售票大厅看到表(一),爸爸对小明说:“我来考考你,你能知道里程与票价之间有何关系吗?”小明点了点头说:“里程与票价是一次函数关系,具体是![]() ”
”
在游船上,他注意到表(二),思考一下,对爸爸说:“若游船在静水中的速度不变,那么我还能算出它的速度和水流速度.”爸爸说:“你真聪明!”亲爱的同学,你知道小明是如何求出的吗?请你和小明一起求出:
(1)票价![]() (元)与里程
(元)与里程![]() (千米)的函数关系式;
(千米)的函数关系式;
(2)游船在静水中的速度和水流速度.
| 里程(千米) | 票价(元) | |
|
| 16 | 38 |
| 甲 丙 | 20 | 46 |
| 甲 丁 | 10 | 26 |
|
|
|
|
表(一)
| 出发时间 | 到达时间 | |
| 甲 乙 |
|
|
| 乙 甲 |
|
|
| 甲 乙 |
|
|
|
|
|
|
表(二)
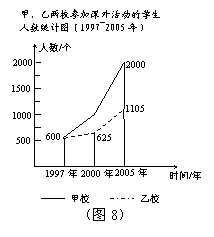
20.(本小题满分8分)下面两幅统计图(如图8、图9),反映了某市甲、乙两所中学学生参加课外活动的情况.请你通过图中信息回答下面的问题.
(1)通过对图8的分析,写出一条你认为正确的结论;(2分)
(2)通过对图9的分析,写出一条你认为正确的结论;(2分)
(3)2005年甲、乙两所中学参加科技活动的学生人数共有多少?(4分
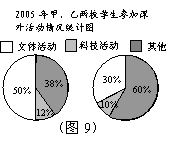
21.(本小题满分10分)在一次数学探究活动中,小强用两条直线把平行四边形![]() 分割成四个部分,使含有一组对顶角的两个图形全等.
分割成四个部分,使含有一组对顶角的两个图形全等.
(1)根据小强的分割方法,你认为把平行四边形分割成满足以上全等关系的直线有 组;(2分)
(2)请在图9的三个平行四边形中画出满足小强分割方法的直线;(6分)
 (3)上述实验操作过程,你发现所画的两条直线有什么规律?(2分)
(3)上述实验操作过程,你发现所画的两条直线有什么规律?(2分)
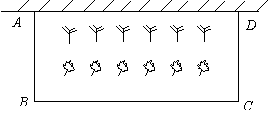 22.(本小题满分12分)在青岛市开展的创城活动中,某居民小区要在一块一边靠墙(墙长15m)的空地上修建一个矩形花园
22.(本小题满分12分)在青岛市开展的创城活动中,某居民小区要在一块一边靠墙(墙长15m)的空地上修建一个矩形花园![]() ,花园的一边靠墙,另三边用总长为40m的栅栏围成(如图所示).若设花园的
,花园的一边靠墙,另三边用总长为40m的栅栏围成(如图所示).若设花园的![]() (m),花园的面积为
(m),花园的面积为![]() (m
(m![]() ).
).
(1)求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)满足条件的花园面积能达到200 m![]() 吗?若能,求出此时
吗?若能,求出此时![]() 的值;若不能,说明理由;
的值;若不能,说明理由;
(3)根据(1)中求得的函数关系式,描述其图象的变化趋势;并结合题意判断当![]() 取何值时,花园的面积最大?最大面积为多少?
取何值时,花园的面积最大?最大面积为多少?
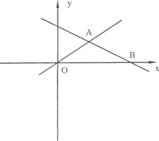
23.(本小题满分12分)在平面直角坐标系xOy中,一次函数y=-![]() x+5的图象交x轴于点B,与正比例函数y=kx(k≠0)的图象交于第一象限内的点A.(如图①)
x+5的图象交x轴于点B,与正比例函数y=kx(k≠0)的图象交于第一象限内的点A.(如图①)
(1)以0、A、B三点为顶点画平行四边形,求这个平行四边形第四个顶点C的坐标;(用含k的代数式表示)
(2)若以0、A、B、C为顶点的平行四边形为矩形,求k的值;(图②备用)
(3)将(2)中的矩形OABC绕点O旋转,使点A落在坐标轴的正半轴上,求所得矩形与原矩形重叠部分的面积.
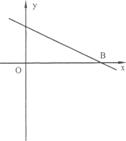
图① 图②
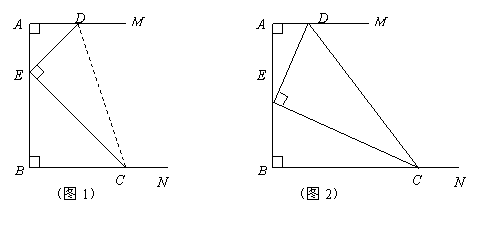
 24.(本小题满分14分)在直角梯形
24.(本小题满分14分)在直角梯形![]() 中,
中,![]() ,顶点
,顶点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上运动(点
上运动(点![]() 不与
不与![]() 重合、点
重合、点![]() 不与
不与 ![]() 重合),
重合),![]() 是
是![]() 边上的动点(点
边上的动点(点![]() 不与
不与![]() 、
、![]() 重合),在运动过程中始终保持
重合),在运动过程中始终保持![]() 且
且![]() .
.
(1)证明:△![]() △
△![]() ;
;
(2)当点![]() 为
为![]() 边的中点时(如图2),求证:①
边的中点时(如图2),求证:①![]() ;
;
②![]() 、
、![]() 分别平分
分别平分![]() 、
、![]() ;
;
(3)设![]() ,请探究:△
,请探究:△![]() 的周长是否与
的周长是否与![]() 值有关,若有关,请用含有m的代数式表示△
值有关,若有关,请用含有m的代数式表示△![]() 的周长;若无关,请说明理由.
的周长;若无关,请说明理由.
 |
 甲 乙
甲 乙