初中毕业生学业考试数学试卷
说明:全卷共8页,考试时间90分钟,满分120分.
| 题号 | 一 | 二 | 三 | 总分 | |||||||||
| 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | ||||
| 得分 | |||||||||||||
一、选择题:每小题3分,共15分;每小题给出四个答案,其中有一个是正确的,把所选答案的编号填写在题目后面的括号内.
1.![]() 等于( )
等于( )
A.2 B.![]() C.
C.![]() D.
D.![]()
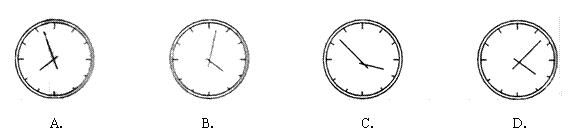
2.小明在镜中看到身后墙上的时钟,实际时间最接近8时的是下图中的( )
3.我市大部分地区今年5月中、下旬的天气情况是:前5天小雨,后5天暴雨.那么能反映我市主要河流水位变化情况的图象大致是( )

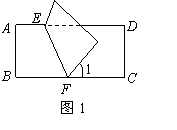 4.如图1,把矩形
4.如图1,把矩形![]() 沿
沿![]() 对折,若
对折,若![]() ,则
,则![]() 等于( )
等于( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5.在同一平面直角坐标系中,直线![]() 与双曲线
与双曲线![]() 的交点个数为( )
的交点个数为( )
A.0个 B.1个 C.2个 D.无法确定
二、填空题:每小题3分,共30分;答案填写在该题的横线上.
6.我市约有495万人口,用科学记数法表示为 人.
7.如果一个几何体的主视图是等腰三角形,那么这个几何体可以是 .(填上满足条件的一个几何体即可)
8.一个袋中装有6个红球、4个黑球、2个白球,每个球除颜色外完全相同,从袋中任意摸出一个球,那么摸出 球的可能性最大.
9.计算:![]() .
.
10.计算:![]() .
.
11.将抛物![]() 向左平移1个单位后,得到的抛物线的解析式是 .
向左平移1个单位后,得到的抛物线的解析式是 .
12.当![]() 时,分式
时,分式![]() 的值为零.
的值为零.
 13.能使平行四边形
13.能使平行四边形![]() 为正方形的条件是
.(填上一个符合题目要求的条件即可)
为正方形的条件是
.(填上一个符合题目要求的条件即可)
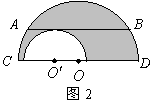
14.如图2,两个半圆中,小圆的圆心![]() 在大
在大![]() 的直径
的直径![]() 上,
上,
长为4的弦![]() 与直径
与直径![]() 平行且与小半圆相切,那么圆中阴影部
平行且与小半圆相切,那么圆中阴影部
分面积等于 .
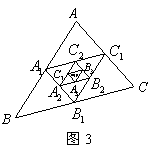 15.如图3,已知
15.如图3,已知![]() 的周长为
的周长为![]() ,分别连接
,分别连接![]()
的中点![]() 得
得![]() ,再连接
,再连接![]() 的中点
的中点
![]() 得
得![]() ,再连接
,再连接![]() 的中点
的中点
![]() 得
得![]() ,这样延续下去,最后得
,这样延续下去,最后得![]() .
.
设![]() 的周长为
的周长为![]() ,
,![]() 的周长为
的周长为![]() ,
,![]() 的周长为
的周长为![]() ,
, ![]() 的周长为
的周长为![]() ,则
,则![]() .
.
三、解答题:本大题有10小题,共75分.
16.本小题满分6分.
因式分解:![]() .
.
17.本小题满分6分.
解不等式组:![]()
18.本小题满分6分.
如图4是某文具店在2005年卖出供学生使用的甲、乙、丙三种品牌科学计算器个数的条形统计图,试解答下面问题:
(1)求卖出甲、乙、丙三种科学计算器的个数的频率;
(2)根据以上统计结果,请你为该文具店进货提出一条合理化建议.
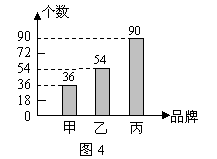 |
19.本小题满分6分.
如图5,已知![]() 的顶点
的顶点![]() 的坐标分别是
的坐标分别是![]() .
.
(1)作出![]() 关于原点
关于原点![]() 中心对称的图形;
中心对称的图形;
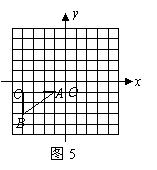 (2)将
(2)将![]() 绕原点
绕原点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 后得到
后得到![]() ,画出
,画出![]() ,并写出点
,并写出点![]() 的坐标.
的坐标.
20.本小题满分7分.
小明与小华在玩一个掷飞镖游戏,如图![]() 甲是一个把两个同心圆平均分成8份的靶,当飞镖掷中阴影部分时,小明胜,否则小华胜(没有掷中靶或掷到边界线时重掷).
甲是一个把两个同心圆平均分成8份的靶,当飞镖掷中阴影部分时,小明胜,否则小华胜(没有掷中靶或掷到边界线时重掷).
(1)不考虑其他因素,你认为这个游戏公平吗?说明理由.
(2)请你在图![]() 乙中,设计一个不同于图
乙中,设计一个不同于图![]() 甲的方案,使游戏双方公平.
甲的方案,使游戏双方公平.
 |
21.本小题满分7分.
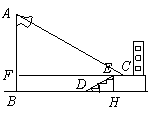
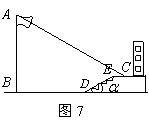 梅华中学九年级数学课外学习小组某下午实践活动课时,测量朝西教学楼前的旗杆
梅华中学九年级数学课外学习小组某下午实践活动课时,测量朝西教学楼前的旗杆![]() 的高度.如图7,当阳光从正西方向照射过来时,旗杆
的高度.如图7,当阳光从正西方向照射过来时,旗杆![]() 的顶端
的顶端![]() 的影子落在教学楼前的坪地
的影子落在教学楼前的坪地![]() 处,测得影长
处,测得影长![]() 与地面的夹角
与地面的夹角![]() .在同一时刻,测得一根长为1m的直立竹竿的影长恰为4m.根据这些数据求旗杆
.在同一时刻,测得一根长为1m的直立竹竿的影长恰为4m.根据这些数据求旗杆![]() 的高度.(可能用到的数据:
的高度.(可能用到的数据:![]() ,结果保留两个有效数字)
,结果保留两个有效数字)
D
22.本小题满分8分.
某公司开发生产的1200件新产品需要精加工后才能投放市场,现有甲、乙两个工厂都想加工这批产品.公司派出相关人员分别到这两间工厂了解生产情况,获得如下信息:
信息一:甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天;
信息二:乙工厂每天比甲工厂多加工20件.
根据以上信息,求甲、乙两个工厂每天分别能加工多少件新产品?
23.本小题满分8分.
用两个全等的正方形![]() 和
和![]() 拼成一个矩形
拼成一个矩形![]() ,把一个足够大的直角三角尺的直角顶点与这个矩形的边
,把一个足够大的直角三角尺的直角顶点与这个矩形的边![]() 的中点
的中点![]() 重合,且将直角三角尺绕点
重合,且将直角三角尺绕点![]() 按逆时针方向旋转.
按逆时针方向旋转.
(1)当直角三角尺的两直角边分别与矩形![]() 的两边
的两边![]() 相交于点
相交于点![]() 时,如图
时,如图![]() 甲,通过观察或测量
甲,通过观察或测量![]() 与
与![]() 的长度,你能得到什么结论?并证明你的结论.
的长度,你能得到什么结论?并证明你的结论.
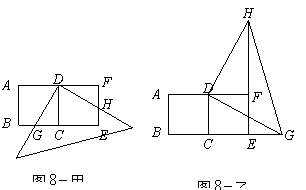 (2)当直角三角尺的两直角边分别与
(2)当直角三角尺的两直角边分别与![]() 的延长线,
的延长线,![]() 的延长线相交于点
的延长线相交于点![]() 时(如
时(如![]() 图乙),你在图
图乙),你在图![]() 甲中得到的结论还成立吗?简要说明理由.
甲中得到的结论还成立吗?简要说明理由.
24.本小题满分10分.
如图9,直线![]() 的解析式为
的解析式为![]() 与
与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() .
.
(1)求原点![]() 到直线
到直线![]() 的距离;
的距离;
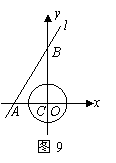 (2)有一个半径为1的
(2)有一个半径为1的![]() 从坐标原点出发,以每秒1个单位长的速度沿
从坐标原点出发,以每秒1个单位长的速度沿![]() 轴正方向运动,设运动时间为
轴正方向运动,设运动时间为![]() (秒).当
(秒).当![]() 与直线
与直线![]() 相切时,求
相切时,求![]() 的值.
的值.
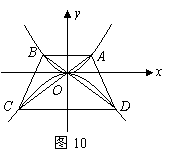
25.本小题满分11分.
如图10,点![]() 在抛物线
在抛物线![]() 上,过点
上,过点![]() 作与
作与![]() 轴平行的直线交抛物线于点
轴平行的直线交抛物线于点![]() ,延长
,延长![]() 分别与抛物线
分别与抛物线![]() 相交于点
相交于点![]() ,连接
,连接![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,且
,且![]() .
.
(1)当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(2)当![]() 为何值时,四边形
为何值时,四边形![]() 的两条对角线互相垂直;
的两条对角线互相垂直;
(3)猜想线段![]() 与
与![]() 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论.
 |
初中毕业生学业考试
数学试卷参考答案及评分意见
一、选择题:每小题3分,共15分
1.D 2.B 3.B 4.A 5.C
二、填空题:每小题3分,共30分
6.![]() ; 7.圆锥或正三棱锥或正四棱锥; 8.红; 9.3 10.
; 7.圆锥或正三棱锥或正四棱锥; 8.红; 9.3 10.![]() ;
;
11.![]() ; 12.
; 12.![]() ; 13.
; 13.![]() 且
且![]() 或
或![]() 且
且![]() 等;
等;
14.![]() ; 15.
; 15.![]() .
.
三、解答下列各题:共75分
16.解:原式![]() ············································································· 2分
············································································· 2分
![]() ····················································································· 4分
····················································································· 4分
![]() ············································································· 6分
············································································· 6分
17.解:由![]() ,得
,得![]() ,······································································· 2分
,······································································· 2分
由![]() ,得
,得![]() ,·············································································· 4分
,·············································································· 4分
![]() 原不等式组的解集是:
原不等式组的解集是:![]() .····························································· 6分
.····························································· 6分
18.解:(1)卖出甲计算器个数的频率:![]() ········································ 2分
········································ 2分
卖出乙计算器个数的频率:![]() ········································· 3分
········································· 3分
卖出丙计算器个数的频率:![]() .····································· 4分
.····································· 4分
(2)![]() ,·············································································· 5分
,·············································································· 5分
![]() 该文具店进甲、乙、丙三种科学计算器时,按
该文具店进甲、乙、丙三种科学计算器时,按![]() 的比例进货.············· 6分
的比例进货.············· 6分
 (或该文具店进货时,丙科学计算器进多一些,而甲、乙科学计算器进少一些.类 似这样的合理答案5分)
(或该文具店进货时,丙科学计算器进多一些,而甲、乙科学计算器进少一些.类 似这样的合理答案5分)
19.(1)正确画出图形·········································································· 3分
(2)正确画出图形·········································································· 5分
![]() ························································································ 6分
························································································ 6分
20.解:(1)这个游戏公平.······························································· 2分
![]() 根据图
根据图![]()
![]() 甲的对称性,阴影部分的面积等于圆面积的一半,
甲的对称性,阴影部分的面积等于圆面积的一半,
![]() 这个游戏公平.·································································································· 4分
这个游戏公平.·································································································· 4分
(2)把图![]() 乙中的同心圆平均分成偶数等分,再把其中的一半作为阴影部分即可.(图略) 7分
乙中的同心圆平均分成偶数等分,再把其中的一半作为阴影部分即可.(图略) 7分
21.解:如图,过点![]() 分别作
分别作![]() 于点
于点![]() 的延长线于
的延长线于![]() .······· 1分
.······· 1分
 在
在![]() 中,
中,
![]()
![]() ,··································································· 2分
,··································································· 2分
![]() m··········································· 3分
m··········································· 3分
又![]() ········································································································· 5分
········································································································· 5分
![]()
![]() .···································································· 6分
.···································································· 6分
![]() .··············································································· 7分
.··············································································· 7分
22.解:设甲工厂每天能加工![]() 件新产品,··································································· 1分
件新产品,··································································· 1分
则乙工厂每天能加工![]() 件新产品.······························································· 2分
件新产品.······························································· 2分
依题意得方程 ![]() .····································································· 4分
.····································································· 4分
解得![]() 或
或![]() (不合题意舍去),····························································· 6分
(不合题意舍去),····························································· 6分
经检验![]() 是所列方程的解,
是所列方程的解,
![]() .····································································································· 7分
.····································································································· 7分
答:甲工厂每天能加工40件新产品,乙工厂每天能加工60件新产品.·················· 8分
23.解:(1)![]() .···························································································· 2分
.···························································································· 2分
![]() 四边形
四边形![]() 和
和![]() 都是正方形,
都是正方形,
![]() ,
,
![]() ,·················· 3分
,·················· 3分
![]() ,
,
![]() ,······································································································· 4分
,······································································································· 4分
![]() .··················································································· 5分
.··················································································· 5分
(2)结论![]() 仍然成立.··················································································· 6分
仍然成立.··················································································· 6分
同理可证![]() ,
,

![]() .······························································ 8分
.······························································ 8分
24.解:(1)在![]() 中,令
中,令![]() ,得
,得![]() ,得
,得![]() .
.
令![]() ,得
,得![]() ,得
,得![]() ,
,
![]() .····················································· 2分
.····················································· 2分
设点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
![]() ,
,
![]() .·························································································· 4分
.·························································································· 4分
(其它解法参照给分)
(2)如图,设![]() 与直线
与直线![]() 相切于点
相切于点![]() ,连
,连![]() ,则
,则![]() ,······························· 5分
,······························· 5分
![]() ,
,
![]()
![]() ······································································· 6分
······································································· 6分
由(1)得![]() ,
,
![]() ,
,
![]() (秒).···························································································· 8分
(秒).···························································································· 8分
根据对称性得![]() ,
,
![]() (秒).························································· 9分
(秒).························································· 9分
![]() 当
当![]() 与直线
与直线![]() 相切时,
相切时,![]() 秒或
秒或![]() 秒.······················································· 10分
秒.······················································· 10分
25.解:(1)![]() 点
点![]() 在抛物线
在抛物线![]() 上,且
上,且![]() ,
,![]() ,······················· 1分
,······················· 1分
![]() 点
点![]() 与点
与点![]() 关于
关于![]() 轴对称,
轴对称,![]() .························································ 2分
.························································ 2分
设直线![]() 的解析式为
的解析式为![]() ,
,
![]() .······················································································· 3分
.······················································································· 3分
解方程组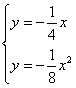 ,得
,得![]() .································································· 4分
.································································· 4分
(2)当四边形![]() 的两对角线互相垂直时,由对称性得直线
的两对角线互相垂直时,由对称性得直线![]() 与
与![]() 轴的夹角等于
轴的夹角等于![]() 所以点
所以点![]() 的纵、横坐标相等,···························································································································· 5分
的纵、横坐标相等,···························································································································· 5分
这时,设![]() ,代入
,代入![]() ,得
,得![]() ,
,![]() .
.
即当![]() 时,四边形
时,四边形![]() 的两条对角线互相垂直.········································· 7分
的两条对角线互相垂直.········································· 7分
(3)线段![]() .································································································ 8分
.································································································ 8分
![]() 点
点![]() 在抛物线
在抛物线![]() ,且
,且![]() ,
,
得直线![]() 的解析式为
的解析式为![]() ,
,
解方程组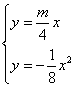 ,得点
,得点![]() ······················································· 9分
······················································· 9分
由对称性得点![]() ,················································· 10分
,················································· 10分
![]() ,
,
![]() .···································································································· 11分
.···································································································· 11分