初中毕业学业考试数学试卷2
| 题号 | 一 | 二 | 三 | 总分 | 合分人 | 复分人 | ||||||
| 19 | 20 | 21 | 22 | 23 | 24 | 25 | ||||||
| 得分 | ||||||||||||
考生注意:1.本卷总分为100分,考试时量为120分钟;2.全卷共有25道题,共8页.
一、填空题(本题共有8个小题,每小题3分,共计24分)
1.![]() .
.
2.某班48名学生的年龄统计结果如下表所示:
| 年龄 | 13 | 14 | 15 | 16 |
| 人数 | 2 | 22 | 23 | 1 |
这个班学生年龄的众数是 .
3.我国南方一些地区的农民戴的斗笠是圆锥形.已知圆锥的母线长为![]() ,底面圆的半
,底面圆的半
 径为
径为![]() ,则圆锥的侧面积为
,则圆锥的侧面积为 ![]() .(结果用
.(结果用![]() 表示)
表示)
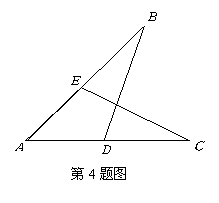
4.如图,![]() ,要使
,要使![]() ,请你增加一个条件是 .(只需要填一个你认为合适的条件)
,请你增加一个条件是 .(只需要填一个你认为合适的条件)
5.若双曲线![]() 过点
过点![]() ,则
,则![]() 的值是 .
的值是 .
6.因季节变换,某商场决定将一服装按标价的![]() 折销售,此时售价为
折销售,此时售价为![]() 元,则该服装的标价为 元.
元,则该服装的标价为 元.
7.按下列规律排列的一列数对:![]() ,
,![]() ,
,![]() ,
,![]() ,则第5个数对中的两个数之和是 .
,则第5个数对中的两个数之和是 .
8.已知![]() 是关于
是关于![]() 的方程
的方程![]() 的两个实数根,则
的两个实数根,则![]() 的最小值是 .
的最小值是 .
二、选择题(每小题有且只有一个正确答案,请将正确答案的选项代号填入下面表格中,每小题3分,共计30分)
| 题次 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 答案 |
9.下列计算正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.![]() 是下列哪一个多项式因式分解的结果( )
是下列哪一个多项式因式分解的结果( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.已知菱形的边长和一条对角线的长均为![]() ,则菱形的面积为( )
,则菱形的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.左图是一几何体,某同学画出它的三视图如下(不考虑尺寸),你认为正确的是( )
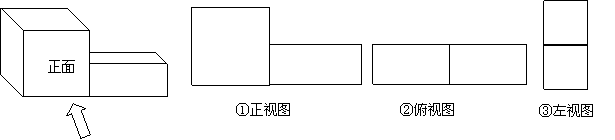
A.①② B.①③ C.②③ D.③
13.不等式组![]() 的解集在数轴上表示正确的是( )
的解集在数轴上表示正确的是( )
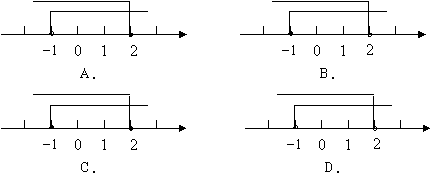 |
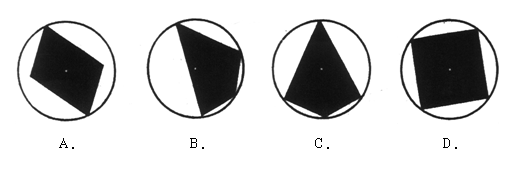 14.下列图形中,既是轴对称图形又是中心对称图形的是( )
14.下列图形中,既是轴对称图形又是中心对称图形的是( )
15.某单位购买甲、乙两种纯净水共用250元,其中甲种水每桶![]() 元,乙种水每桶
元,乙种水每桶![]() 元;乙种水的桶数是甲种水桶数的
元;乙种水的桶数是甲种水桶数的![]() .设买甲种水
.设买甲种水![]() 桶,买乙种水
桶,买乙种水![]() 桶,则所列方程组中正确的是( )
桶,则所列方程组中正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
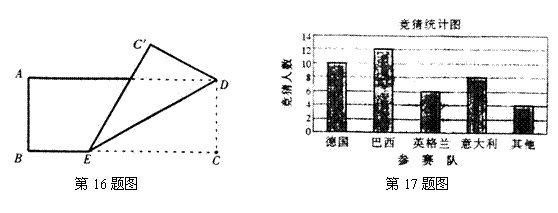
16.将一张矩形纸片![]() 如图所示折叠,使顶点
如图所示折叠,使顶点![]() 落在
落在![]() 点.已知
点.已知![]() ,
,![]() ,则折痕
,则折痕![]() 的长为( )
的长为( )
 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
17.2006年6月,世界杯足球赛决赛在德国拉开战幕,6月5日,某班40名学生就哪支队伍将夺冠进行竞猜,统计结果如图.若把认为巴西队将夺冠的这组学生人数作为一组的频数,则这一组的频率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
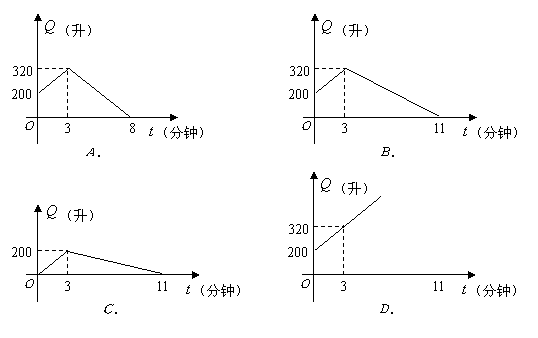 18.一个装有进出水管的水池,单位时间内进、出水量都是一定的.已知水池的容积为
18.一个装有进出水管的水池,单位时间内进、出水量都是一定的.已知水池的容积为![]() 升,又知单开进水管20分钟可把空水池注满;若同时打开进、出水管,20分钟可把满水池的水放完,现已知水池内有水
升,又知单开进水管20分钟可把空水池注满;若同时打开进、出水管,20分钟可把满水池的水放完,现已知水池内有水![]() 升,先打开进水管
升,先打开进水管![]() 分钟,再打开出水管,两管同时开放,直至把水池中的水放完,则能确定反映这一过程中水池的水量
分钟,再打开出水管,两管同时开放,直至把水池中的水放完,则能确定反映这一过程中水池的水量![]() (升)随时间
(升)随时间![]() (分钟)变化的函数图象是( )
(分钟)变化的函数图象是( )
三、解答题(本大题共7个小题,要求写出详细的演算过程或推理过程,否则不予给分,共计46分)
19.(本题满分6分,每小题3分)
(1)计算:![]()
(2)解方程:![]()
20.(本题满分6分)先化简,再求值:
![]() 其中
其中![]()
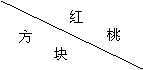
21.(本题满分6分)如图,是从一副扑克牌中取出的两组牌,分别是红桃1,2,3和方块1,2,3,将它们的背面朝上分别重新洗牌后,再从两组牌中各摸出一张.
|
(2)求摸出的两张牌的牌面数字之和不小于5的概率.
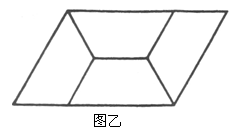
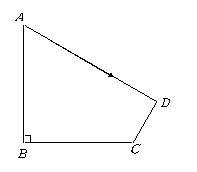
22.(本题满分6分)如图甲,四边形![]() 是等腰梯形,
是等腰梯形,![]() .由4个这样的等腰梯形可以拼出图乙所示的平行四边形.
.由4个这样的等腰梯形可以拼出图乙所示的平行四边形.
(1)求梯形![]() 四个内角的度数;
四个内角的度数;
(2)试探梯形![]() 四条边之间存在的数量关系,并说明理由.
四条边之间存在的数量关系,并说明理由.
 | |||
 | |||
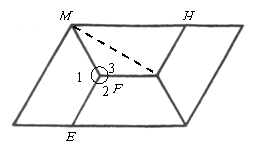
23.(本题满分6分)如图,小鹏准备测量学校旗杆的高度.他发现当斜坡正对着太阳时,旗杆![]() 的影子恰好落在水平地面
的影子恰好落在水平地面![]() 和斜坡坡面
和斜坡坡面![]() 上,测得旗杆在水平地面上的影长
上,测得旗杆在水平地面上的影长![]() 米,在斜坡坡面上的影长
米,在斜坡坡面上的影长![]() 米,太阳光线
米,太阳光线![]() 与水平地面成
与水平地面成![]() 角,且太阳光线
角,且太阳光线![]() 与斜坡坡面
与斜坡坡面![]() 互相垂直.请你帮小鹏求出旗杆
互相垂直.请你帮小鹏求出旗杆![]() 的高度(精确到1米).
的高度(精确到1米).
 (可供选用数据:取
(可供选用数据:取![]() ,
,![]() )
)
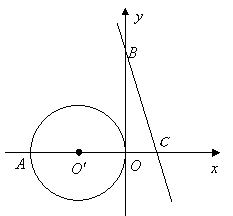
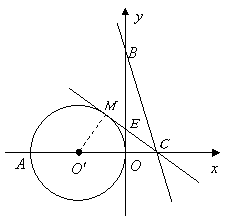
24.(本题满分7分)如图,在直角坐标系中,点![]() 的坐标为
的坐标为![]() ,
,![]() 与
与![]() 轴相交于原点
轴相交于原点![]() 和点
和点![]() ,又
,又![]() 两点的坐标分别为
两点的坐标分别为![]() ,
,![]() .
.
(1)当![]() 时,求经过
时,求经过![]() 两点的直线的解析式;
两点的直线的解析式;
(2)当![]() 点在
点在![]() 轴上运动时,直线
轴上运动时,直线![]() 与
与![]() 有哪几种位置关系?并求每种位置关系时
有哪几种位置关系?并求每种位置关系时![]() 的取值范围.
的取值范围.
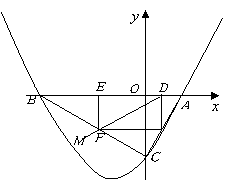
25.(本题满分9分)如图:已知抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴 交于点
轴 交于点![]() ,
,![]() 为坐标原点.
为坐标原点.
(1)求![]() 三点的坐标;
三点的坐标;
(2)已知矩形![]() 的一条边
的一条边![]() 在
在![]() 上,顶点
上,顶点![]() 分别在
分别在![]() ,
,![]() 上,设
上,设![]() ,矩形
,矩形![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式,并指出
的函数关系式,并指出![]() 的取值范围;
的取值范围;
(3)当矩形![]() 的面积
的面积![]() 取最大值时,连结对角线
取最大值时,连结对角线![]() 并延长至点
并延长至点![]() ,使
,使![]() .
.
 试探究此时点
试探究此时点![]() 是否在抛物线上,请说明理由.
是否在抛物线上,请说明理由.
初中毕业学业考试试卷
数学参考答案及评分标准
一、填空题
1.![]() 2.15 3.
2.15 3.![]() 4.
4.![]()
5.6 6.30 7.27 8.![]()
二、选择题
| 题次 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 答案 | A | C | C | A | B | D | A | C | D | B |
三、解答题
19.(1)解:原式![]() ·············································································· 2分
·············································································· 2分
![]() ··································································································· 3分
··································································································· 3分
(2)解:去分母得:![]() ··································································· 1分
··································································· 1分
解之得![]() ································································································· 2分
································································································· 2分
经检验,![]() 是原方程的根········································································· 3分
是原方程的根········································································· 3分
20.(1)所有可能出现的结果可用下表表示:
|
| 1 | 2 | 3 |
| 1 |
|
|
|
| 2 |
|
|
|
| 3 |
|
|
|
···································································································································· 4分
(2)由上表可知牌面的数字之和不小于5的概率为:![]() .······································ 6分
.······································ 6分
 22.解:(1)如图
22.解:(1)如图![]() ,
,![]() ,即
,即![]() ,所以图甲中梯形的上底角均为
,所以图甲中梯形的上底角均为![]() ,下底角均为
,下底角均为![]() .·············································· 3分
.·············································· 3分
(2)由![]() 既是梯形的腰,又是梯形的上底可知,梯形的腰等于上底.连结
既是梯形的腰,又是梯形的上底可知,梯形的腰等于上底.连结![]() ,则
,则![]() ,从而
,从而![]() ,
,![]() ,所以
,所以![]() ,因此梯形的上底等于下底长的一半,且等于腰长. 6分
,因此梯形的上底等于下底长的一半,且等于腰长. 6分
23.解:延长![]() ,
,![]() 相交于点
相交于点![]() ,则
,则![]() ,,
,,![]() .···························· 2分
.···························· 2分
在![]() A中,
A中,![]() ,由
,由![]() ,
,
得![]() ································································ 5分
································································ 5分
答:![]() ·················································································································· 6分
·················································································································· 6分
24.解:(1)经过![]() 两点的直线的解析式为:
两点的直线的解析式为:![]() ····································· 3分
····································· 3分
 (2)点
(2)点![]() 在
在![]() 轴上运动时,直线
轴上运动时,直线![]() 与
与![]() 的位置关系有相离、相切、相交三种. 4分
的位置关系有相离、相切、相交三种. 4分
当点![]() 在
在![]() 轴上运动到点
轴上运动到点![]() 时,恰好使直线
时,恰好使直线![]() 切
切![]() 于点
于点![]() ,连结
,连结![]() ,则
,则![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,
由![]() ,可得
,可得![]() ,
,
![]() ,······························································································ 6分
,······························································································ 6分
由圆的对称性可知,当![]() 时,直线
时,直线![]() 与圆相切;当
与圆相切;当![]() 或
或![]() 时,直线
时,直线![]() 与圆相离;当
与圆相离;当![]() 时,直线
时,直线![]() 与圆相交.···················································· 7分
与圆相交.···················································· 7分
25.解:(1)![]() ,
,![]() ,
,![]() ································································ 3分
································································ 3分
(2)由![]() ,可得
,可得![]() ,
,![]() ·················· 4分
·················· 4分
由![]() 得
得![]() ,又
,又![]() ,
,![]() ,
,![]() 5分
5分
![]()
![]() 与
与![]() 的函数关系式为
的函数关系式为![]() ,且
,且![]() .························ 6分
.························ 6分
(3)由![]() 可知
可知![]() 时,
时,![]() 有最大值10,此时
有最大值10,此时![]() ,
,![]() ,
,![]() . 7分
. 7分
过点![]() 作
作![]() ,垂足为
,垂足为![]() ,则有
,则有![]() ,
,![]() ,又有
,又有![]() ,得
,得![]() ,
,![]()
![]() ,
,![]() ····························································· 8分
····························································· 8分
在二次函数![]() 中,当
中,当![]() 时,
时,![]() ,
,
![]() 点
点![]() 不在抛物线上. 9分
不在抛物线上. 9分