初中毕业学业考试数学试卷
一、填空题(本题满分24分,共8小题,每小题3分)
1.![]() 的倒数是
.
的倒数是
.
2.因式分解:![]() .
.
3.我国2006年第一季度实现了GDP(国民生产总值)43390亿元,用科学记数法表示为 亿元.
4.点![]() 在一次函数
在一次函数![]() 的图象上,则
的图象上,则![]() .
.
5.如图1,将一副七巧板拼成一只小动物,则![]() .
.

6.在![]() 中,
中,![]() .则
.则![]() .
.
7.容量是56升的铁桶,装满油,取出![]() 升后,桶内还剩油
升.
升后,桶内还剩油
升.
8.如图2,是一个圆形转盘,现按![]() 分成四个部分,分别涂上红,黄,蓝,绿四种颜色,自由转动转盘,停止后指针落在绿色区域的概率为
.
分成四个部分,分别涂上红,黄,蓝,绿四种颜色,自由转动转盘,停止后指针落在绿色区域的概率为
.
二、选择题(本题满分30分,共10小题,每小题3分)
9.16的算术平方根是( )
A.4 B.![]() C.8 D.
C.8 D.![]()
10.要使二次根式![]() 有意义,
有意义,![]() 应满足的条件是( )
应满足的条件是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.分式![]() 的值为1时,
的值为1时,![]() 的值是( )
的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.一次数学测试后,随机抽取九年级二班5名学生的成绩如下:78,85,91,98,98.关于这组数据的错误说法是( )
A.极差是20 B.众数是98 C.中位数是91 D.平均数是91
13.圆![]() 的直径为12cm,圆心
的直径为12cm,圆心![]() 到直线
到直线![]() 的距离为7cm,则直线
的距离为7cm,则直线![]() 与圆
与圆![]() 的位置关系是( )
的位置关系是( )
A.相交 B.相切 C.相离 D.不能确定
14.从左边看图3中的物体,得到的图形是( )

15.下列运算正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
16.下列说法不正确的是( )
A.方差反映了一组数据与其平均数的偏离程度
B.为了解一种灯泡的使用寿命,宜采用普查的方法
C.必然事件的概率为1
D.对于简单随机样本,可以用样本的方差去估计总体的方差
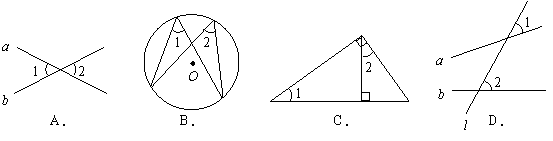 17.下列图形中,
17.下列图形中,![]() 与
与![]() 不一定相等的是( )
不一定相等的是( )
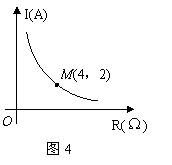 18.某闭合电路中,电源电压不变,电流
18.某闭合电路中,电源电压不变,电流![]() 与电阻R(
与电阻R(![]() )成反比例,图4表示的是该电路中电流I与电阻R之间函数关系的图象,则用电阻R
)成反比例,图4表示的是该电路中电流I与电阻R之间函数关系的图象,则用电阻R
表示电流I的函数解析式为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
三、解答题(本题满分24分,共4小题,其中19题5分,20题7分,21题5分,22题7分)
19.解方程:![]()
20.如今,餐馆常用一次性筷子,有人说这是浪费资源,破坏生态环境.已知用来生产一次性筷子的大树的数量(万棵)与加工后一次性筷子的数量(亿双)成正比例关系,且100万棵大树能加工成18亿双一次性筷子.
(1)求用来生产一次性筷子的大树的数量![]() (万棵)与加工后一次性筷子的数量
(万棵)与加工后一次性筷子的数量![]() (亿双)的函数关系式.
(亿双)的函数关系式.
(2)据统计,我国一年要耗费一次性筷子约450亿双,生产这些一次性筷子约需要多少万棵大树?每1万棵大树占地面积约为0.08平方千米,照这样计算,我国的森林面积每年因此将会减少大约多少平方千米?
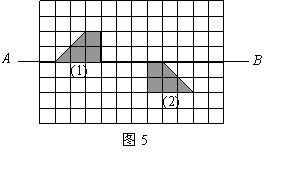 21.如图5方格中,有两个图形.
21.如图5方格中,有两个图形.
(1)画出图形(1)向右平移7个单位的像![]() ;
;
(2)画出像![]() 关于直线
关于直线![]() 轴反射的像
轴反射的像![]() ;
;
(3)将像![]() 与图形(2)看成一个整体图形,请写出这个整体图形的对称轴的条数.
与图形(2)看成一个整体图形,请写出这个整体图形的对称轴的条数.
22.售货员:“快来买啦,特价鸡蛋,原价每箱14元,现价每箱12元,每箱有鸡蛋30个.”
顾客甲:“我店里买了一些这种特价鸡蛋,花的钱比按原价买同样多鸡蛋花的钱的2倍少96元.”
乙顾客:“我家买了两箱相同特价的鸡蛋,结果18天后,剩下的20个鸡蛋全坏了.”
请你根据上面的对话,解答下面的问题:
(1)顾客乙买的两箱鸡蛋合算吗?说明理由.
(2)请你求出顾客甲店里买了多少箱这种特价鸡蛋,假设这批特价鸡蛋的保质期还有18天,那么甲店里平均每天要消费多少个鸡蛋才不会浪费?
四、证明题(本题满分6分)
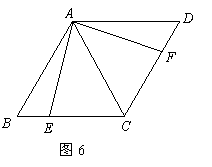 23.如图6,菱形
23.如图6,菱形![]() 中,
中,![]() 分别为
分别为![]() 上的点,且
上的点,且![]() .求证:
.求证:![]() .
.
五、应用题(本题满分6分)
24.甲、乙两超市同时开业,为了吸引顾客,都举行有奖酬宾活动:凡购物满100元,均可得到一次摸奖的机会,在一个纸盒里装有2个红球和2个白球,除颜色外,其它全部相同,摸奖者一次从中摸出两个球,根据球的颜色决定送礼金券的多少(如下表).
甲超市
| 球 | 两红 | 一红一白 | 两白 |
| 礼金券(元) | 5 | 10 | 5 |
乙超市
| 球 | 两红 | 一红一白 | 两白 |
| 礼金券(元) | 10 | 5 | 10 |
如果只考虑中奖因素,你将会选择去哪个超市购物?请说明理由.
六、综合题(本题满分10分)
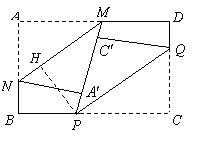
25.如图7,矩形纸片![]() 的边长分别为
的边长分别为![]() .将纸片任意翻折(如图8),折痕为
.将纸片任意翻折(如图8),折痕为![]() .(
.(![]() 在
在![]() 上),使顶点
上),使顶点![]() 落在四边形
落在四边形![]() 内一点
内一点![]() ,
,![]() 的延长线交直线
的延长线交直线![]() 于
于![]() ,再将纸片的另一部分翻折,使
,再将纸片的另一部分翻折,使![]() 落在直线
落在直线![]() 上一点
上一点![]() ,且
,且![]() 所在直线与
所在直线与![]() 所在直线重合(如图9)折痕为
所在直线重合(如图9)折痕为![]() .
.
(1)猜想两折痕![]() 之间的位置关系,并加以证明.
之间的位置关系,并加以证明.
(2)若![]() 的角度在每次翻折的过程中保持不变,则每次翻折后,两折痕
的角度在每次翻折的过程中保持不变,则每次翻折后,两折痕![]() 间的距离有何变化?请说明理由.
间的距离有何变化?请说明理由.
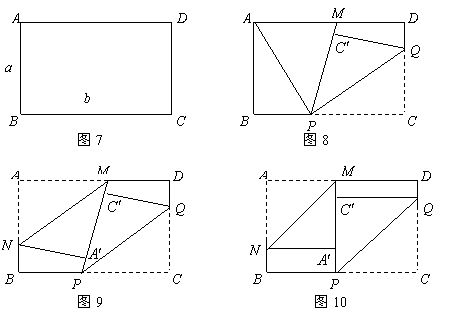 (3)若
(3)若![]() 的角度在每次翻折的过程中都为
的角度在每次翻折的过程中都为![]() (如图10),每次翻折后,非重叠部分的四边形
(如图10),每次翻折后,非重叠部分的四边形![]() ,及四边形
,及四边形![]() 的周长与
的周长与![]() 有何关系,为什么?
有何关系,为什么?
附加题:
七、选择题(本题满分10分,共2小题,每小题5分)
26.在![]() 中,
中,![]() 的长分别是方程
的长分别是方程![]() 的两个根,
的两个根,![]() 内一点
内一点![]() 到三边的距离都相等.则
到三边的距离都相等.则![]() 为( )
为( )
A.1 B.![]() C.
C.![]() D.
D.![]()
 27.如图11,两个半圆,大半圆中长为16cm的弦
27.如图11,两个半圆,大半圆中长为16cm的弦![]() 平行于直径
平行于直径![]() ,且与小半圆相切,则图中阴影部分的面积为( )
,且与小半圆相切,则图中阴影部分的面积为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
八、综合题(本题满分20分,28题9分,29题11分)
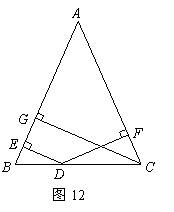
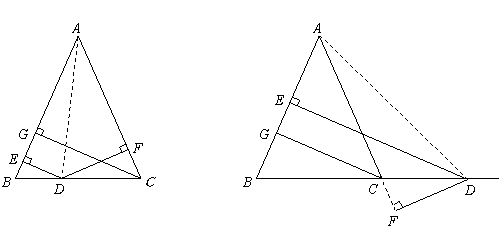
28.如图12,在![]() 中,
中,![]() 是
是![]() 上任意一点,过
上任意一点,过![]() 分别向
分别向![]() 引垂线,垂足分别为
引垂线,垂足分别为![]() 是
是![]() 边上的高.
边上的高.
(1)![]() 的长之间存在着怎样的等量关系?并加以证明.
的长之间存在着怎样的等量关系?并加以证明.
 (3)若
(3)若![]() 在底边的延长线上,(1)中的结论还成立吗?若不成立,又存在怎样的关系?请说明理由.
在底边的延长线上,(1)中的结论还成立吗?若不成立,又存在怎样的关系?请说明理由.
29.已知抛物线![]() 经过
经过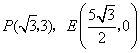 及原点
及原点![]() .
.
(1)求抛物线的解析式.
(2)过![]() 点作平行于
点作平行于![]() 轴的直线
轴的直线![]() 交
交![]() 轴于
轴于![]() 点,在抛物线对称轴右侧且位于直线
点,在抛物线对称轴右侧且位于直线![]() 下方的抛物线上,任取一点
下方的抛物线上,任取一点![]() ,过点
,过点![]() 作直线
作直线![]() 平行于
平行于![]() 轴交
轴交![]() 轴于
轴于![]() 点,交直线
点,交直线![]() 于
于![]() 点,直线
点,直线![]() 与直线
与直线![]() 及两坐标轴围成矩形
及两坐标轴围成矩形![]() (如图13).是否存在点
(如图13).是否存在点![]() ,使得
,使得![]() 与
与![]() 相似?若存在,求出
相似?若存在,求出![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
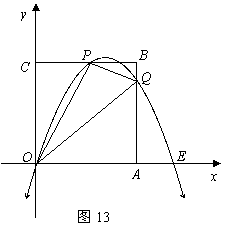 (3)如果符合(2)中的
(3)如果符合(2)中的![]() 点在
点在![]() 轴的上方,连结
轴的上方,连结![]() ,矩形
,矩形![]() 内的四个三角形
内的四个三角形![]() 之间存在怎样的关系?为什么?
之间存在怎样的关系?为什么?
初中毕业学业考试
参考答案及评分标准
一、填空题(每小题3分,共24分)
1.2 2.![]() 3.
3.![]() 4.
4.![]() 5.
5.![]() 6.
6.![]()
7.![]() 或
或![]() 8.
8.![]()
二、选择题(每小题3分,共30分)
9.A 10.A 11.C 12.D 13.C 14.B 15.C 16.B 17.D 18.A
三、解答题(第19题5分,第20题7分,第21题6分,第22题8分)
19.![]()
20.(1)设![]() ,由题意得:
,由题意得:![]() ,求得
,求得![]()
所以用来加工一次性筷子的大树的数量![]() (万棵)与加工后筷子的数量
(万棵)与加工后筷子的数量![]() (亿双)的函数关系式为
(亿双)的函数关系式为![]()
(2)当![]() 时,
时,![]() ,
,![]() 平方千米.
平方千米.
答:略
21.(1)图略; (2)图略; (3)2条.
22.(1)顾客乙买两箱鸡蛋节省的钱![]() (元)
(元)
顾客乙丢掉的20个坏鸡蛋浪费的钱![]() (元)
(元)
因为4元![]() 8元, 所以顾客乙买的两箱鸡蛋不合算.
8元, 所以顾客乙买的两箱鸡蛋不合算.
(2)设顾客甲买了![]() 箱鸡蛋. 由题意得:
箱鸡蛋. 由题意得:![]() .
.
解这个方程得:![]() ,
,![]() (个)
(个)
答:略
四、证明题(6分)
23.因为四边形![]() 是菱形,所以
是菱形,所以![]()
因为![]() ,所以
,所以![]()
在![]() 与
与![]() 中,
中,
因为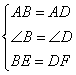 ,所以
,所以![]() 所以
所以![]() .
.
五、应用题(5分)
24.去甲超市购物一次摸奖获10元礼金券的概率是![]() (甲)
(甲)![]()
去乙超市购物一次摸奖获10元礼金券的概率是![]() (乙)
(乙)![]()
所以我选择去甲超市购物.
六、综合题(10分)
25.(1)![]()
因为四边形![]() 是矩形,所以
是矩形,所以![]() ,且
,且![]() 在
在![]() 直线上,则有
直线上,则有![]()
所以![]() ,由翻折可得:
,由翻折可得:![]() ,
,
![]() ,所以
,所以![]() ,故
,故![]() .
.
(2)两折痕![]() 间的距离不变
间的距离不变
过![]() 作
作![]() ,则
,则![]() ,
,
因为![]() 的角度不变,所以
的角度不变,所以![]() 的角度也不变,则所有的
的角度也不变,则所有的![]() 都是平行的
都是平行的
又因为![]() ,所以所有的
,所以所有的![]() 都是相等的
都是相等的
又因为![]() ,故
,故![]() 的长不变.
的长不变.
 (3)当
(3)当![]() 时,四边形
时,四边形![]() 是正方形,
是正方形,
四边形![]() 是矩形.
是矩形.
因为![]() ,
,![]() ,
,
所以矩形![]() 的周长为
的周长为![]() .
.
同理可得矩形![]() 的周长为
的周长为![]() ,所以两个四边形的周长都为
,所以两个四边形的周长都为![]() ,与
,与![]() 无关.
无关.
附加题:
七、选择题(每小题5分,共10分)
26.B 27.C
八、综合题(第28题9分,第29题11分)
28.解:(1)![]()
证明:连结![]() ,则
,则![]() ,即
,即![]()
 因为
因为![]() ,所以
,所以![]()
(2)当点![]() 在
在![]() 延长线上时,
延长线上时,
(1)中的结论不成立,有![]() .
.
理由:连结![]() ,则
,则![]() ,即有,
,即有,![]()
因为![]() ,所以
,所以![]() ,即
,即![]() .
.
当![]() 点在
点在![]() 的延长线上时,则有
的延长线上时,则有![]() ,说明方法同上.
,说明方法同上.
29.解:(1)由已知可得:
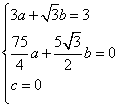 解之得,
解之得,![]() .
.
因而得,抛物线的解析式为:![]() .
.
(2)存在.
设![]() 点的坐标为
点的坐标为![]() ,则
,则![]() ,要使
,要使![]() ,则有
,则有![]() ,即
,即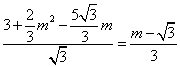 ,解之得,
,解之得,![]() .
.
当![]() 时,
时,![]() ,即为
,即为![]() 点,所以得
点,所以得![]()
要使![]() ,则有
,则有![]() ,即
,即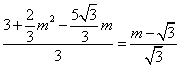
解之得,![]() ,当
,当![]() 时,即为
时,即为![]() 点,
点,
当![]() 时,
时,![]() ,所以得
,所以得![]() .故存在两个
.故存在两个![]() 点使得
点使得![]() 与
与![]() 相似.
相似.
![]() 点的坐标为
点的坐标为![]() .
.
(3)在![]() 中,因为
中,因为![]() .所以
.所以![]() .
.
当![]() 点的坐标为
点的坐标为![]() 时,
时,![]() .
.
所以![]() .
.
因此,![]() 都是直角三角形.
都是直角三角形.
又在![]() 中,因为
中,因为![]() .所以
.所以![]() .
.
即有![]() .
.
所以![]() ,又因为
,又因为![]()
![]() ,所以
,所以![]() .
.