初中学业水平测试卷数学试题(一)
一、选择题(每小题4分，共40分)
1.已知a、b都是有理数，且∣a∣= a，∣b∣≠b，则ab是（ ）
A．负数 B.正数 C.负数或零 D.非负数.
2. 把a3－ab2分解因式的正确结果是（ ）
A.(a+ab)(a－ab) B.a (a2－b2) C.a(a+b)(a－b) D.a(a－b)2
3.不用查表，就可以估计出
的数值在（ ）
A.42~43之间 B.43~44之间 C.44~45之间 D.45~46之间
4、在△ABC中，AB=AC=3，BC=2，则S△ABC等于 （ ）
A、3 B、2
C、2
D、3
5.抛物线y=x2-4x+3的顶点坐标是 （ ）
A．(2，7) B．(2，-1) D．(-2，7) D．(-2，-1)
6. 合肥“商之都”家电部，把甲、乙两种品牌的空调连续三年的销售情况制成不同的两种图（如下图），从图中可以看出两种品牌的空调销售量的增幅（ ）
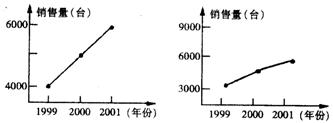
A.甲>乙 B.甲=乙 C.甲<乙 D.不能确定
7.如图，E、F、G、H分别是四边形ABCD四条边的中点，要使四边形EFGH为矩形，四边形ABCD应具备的条件是（ ）.
A.一组对边平行而另一组对边不平行 B.对角线相等
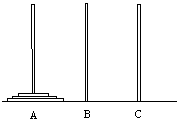C.对角线互相垂直
D.对角线互相平分
 |  | ||
(第7题图) (第9题图) (第10题图)
8.水果店用1000元购进一批草霉，当天售出，获利10％，过几天后又以上次售出价的90％购进同样的草霉，由于大气变化卖不出去，一天后将这批草霉按第二次购进价的九折（即90％）降价售出．这样、这家水果店在这两次交易中（ ）
A.赢亏平衡 B.赢利1元 C.赢利9元 D.亏本1.1元
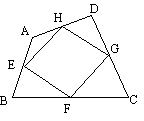
9.如图，四个半径均为R的等圆彼此相切，则图中阴影部分（形似水壶）图形的面积为
A.4R2 B.πR2 C.2πR2 D.4πR2
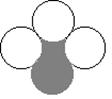
10.如图A、B、C是固定在桌面上的三根立柱，其中A柱上穿有三个大小不同的圆片，下面的直径总比上面的大．现想将这三个圆片移动到B柱上，要求每次只能移动一片（叫移动一次），被移动的圆片只能放入A、B、C三个柱之一且较大的圆片不能叠在小片的上面，那么完成这件事情至少要移动圆片的次数是
A.6 B.7 C.8 D.9
二、填空题(每小题4分，共20分)
11.
的倒数是
.
12.已知点P（－2，3），则点P关于x轴对称的点坐标是 .
13.在高为h的山坡上测得一建筑物顶端与底部的俯角分别是30°和60°，用h表示建筑物的高度为 (用含h的代数式表示).
14.某市民政部门今年元宵节期间举行了“即开式社会福利彩票”销售活动，设置彩票3000万张（每张彩票2元），在这些彩票中，设置了如下的奖次：
| 奖金(万元) | 50 | 15 | 8 | 4 | … |
| 数量(个) | 20 | 20 | 20 | 180 | … |
如果花2元钱购买1张彩票，那么能得到8万元以上(包括8万元)大奖的概率是 .
15.如图，在等腰梯形ABCD中，AB∥CD，DC=3 cm，∠A=60°,BD平分∠ABC，则这个梯形的周长是_____ _.
三、(每小题8分，共16分)
16.计算：-32+(
)-2+
-(1-
)0
17.解不等式
，并把它的解集在数轴上表示出来.
四、(每小题9分，共18分)
18.已知:反比例函数y=
和一次函数y=2x -1，其中一次函数的图像经过点（k，5）.
(1)试求反比例函数的解析式；
(2)若点A在第一象限，且同时在上述两函数的图像上，求A点的坐标。
19. 某校在一次考试中，甲乙两班学生的数学成绩统计如下：
| 分数 | 50 | 60 | 70 | 80 | 90 | 100 | |
| 人数 | 甲 | 1 | 6 | 12 | 11 | 15 | 5 |
| 乙 | 3 | 5 | 15 | 3 | 13 | 11 | |
请根据表格提供的信息回答下列问题：
(1)甲班众数为______分，乙班众数为_______分，从众数看成绩较好的是_____班.
(2)甲班的中位数是_______分，乙班的中位数是______分.
(3)若成绩在85分以上为优秀，则成绩较好的是______班.
五、(每小题10分，共20分)
20.如图，⊙O表示一圆形纸板，根据要求，需通过多次剪裁，把它剪成若干个扇形面，操作过程如下：第一次剪裁，将圆形纸板等分为4个扇形；第二次剪裁，将上次得到的扇形面中的一个再等分成4个扇形；以后按第2次剪裁的作法进行下去．
（1）请你在⊙O中，用尺规作出第2次剪裁后得到的7个扇形（保留痕迹，不写作法）
（2）请你通过操作和猜想，将第3、第4和第n次剪裁后所得扇形的总个数（s）填人下表．
（3）请你推断，能不能按上述操作过程，将原来的圆形纸板剪成33个扇形？为什么？
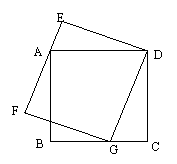21.如图，G是边长为a的正方形ABCD的边BC上一点，矩形DEFG的边EF过点A.
(1)设DG=x，FG=y，求y与x的函数关系式；
(2)若正方形ABCD的边长为4，GD=5，求FG的长.
六、(本题满分12分)
22. 某公司进行股份制改造，设内部职工股M股，计划由公司职工平均投资入股．如果职工中有4人愿意投资10万元，那么其余的职工平均每人可以少投资0.5万元；如果职工中有6人愿意每人投资12万元，那么其余的职工平均每人可以少投资1万元． 如果职工中有10人不参加投资人股，那么其余的职工平均每人需投资多少万元？
七、(本题满分12分)
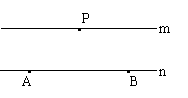
23. 如图，已知直线m∥n，m与n之间的距离为3，A、B为直线n上的两定点，AB=8，P为直线m上的一动点。
(1)当P点在m上移动时，△ABP的面积有何变化？简述理由；
(2)当点P在m上移动时，△ABP的周长有没有变化？m上是否存在一点P，使得△ABP的周长最小？若存在，请你建立用适当的直角坐标系求出点P的坐标，并求△ABP周长的最小值；若不存在，请说明理由.
 |
八、(本题满分12分)
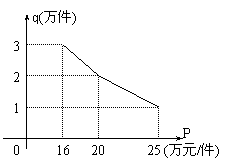24.某企业将经营状态良好某种消费品以58万元的优惠价转让给企业乙，约定乙用经营该店利润偿还转让费（不计息），已知经营该店固定成本为6.8万元/月，该消费品进价为16元/件，月销售q（万件）与售价p元/件关系如图：
(1)写出销量q与售价p的函数关系式；
(2)售价定为多少月利润最多？
(3)企业最早可望经营专卖店几月还清转让费？