初三数学试题
（满分：150分；考试时间：120分钟）
| 题 号 | 一 | 二 | 三 | 总 分 | |||||||||
| 1—12 | 13—18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | ||
| 得分 | |||||||||||||
一、填空题（每小题3分，共36分）
1．当x 时，分式
有意义。
2．将0.000702用科学记数法表示,结果为___________。
3．计算
=
。
4．方程
的解是
________。
5．抛物线
的顶点坐标是______ 。
6．已知圆柱的底面半径为2cm，母线长为3cm，则该圆柱的侧面展开
图的面积为 cm
.
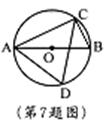
7．如图，△
为⊙O的内接三角形，AB为⊙O的直径，点D在
⊙O 上，∠BAC＝35°，则∠ADC＝ 度．
8．某型号的手机连续两次降价，每个售价由原来的1185元降到580元，设平均每次降价的百分率为
，则可列出的方程是____________________。
9．若抛物线
，开口向下，且顶点经过原点，则ｋ＝_______。
10．抛物线
向上平移2个单位长度后得到新抛物线的解析式为____________。
11．在一个不透明的箱子里放有除颜色外，其余都相同的5 个小球，其中红球3个、
白球2个．搅匀后，从中同时摸出1个小球是白球的概率是 。
12．已知二次函数的图象开口向上,且与y轴的正半轴相交,请写出一个满足条件的表达式
为 。
二、选择题（每小题4分，共24分，单项选择）.
13．下列运算中，结果正确的是（ ）
A.
B.
C.
D.
．
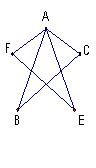
14．.如图△ABC≌△AEF，AB=AE，AC=AF，那么∠EAC= （ ）
A. ∠ACB B. ∠BAF C. ∠CAF D. ∠BAC
15．下列调查，比较适用普查而不适用抽样调查方式的是（ ）
A．调查全省食品市场上某种食品的色素含量是否符合国家标准；
B．调查一批灯泡的使用寿命；
C．调查你所在班级全体学生的身高；
D．调查全国初中生每人每周的零花钱数
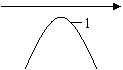
16．
|
|
|
|
函数
的图象大致为 （ ）
 | |||||||
 | |||||||
 | |||||||
 | |||||||
|
|
|
|
|
|
|
|
A B C D
17．已知两圆的半径分别为1和4，圆心距为3，则两圆的位置关系是（ ）
A．外离； B．外切； C．相交； D．内切.
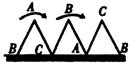18．一块等边三角形的木板，边长为1，现将木板沿水平线翻滚（如图），那么B点从开始至结束所走过的路径长度为（ ）
A．
B．
C．4 D．2＋
三、解答题（共90分）.
19．（8分）计算：
.
20．（8分）.先化简，再求值(
+
)÷
，其中
21．（8分）解方程：
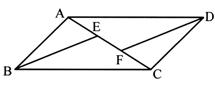
22.（8分）如图，在口ABCD中，E、F是对角线AC上的两点，AE＝CF，求证：BE＝DF.
 |
23．（8分）如图，已知直线AB经过⊙O上的点Ａ，且AB=OA,∠ OBA=450。
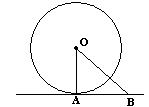试判断：直线AB是⊙O的切线吗？请说明理由。
24．（8分）已知抛物线
的图象经过点(1,4)、(-1，－2），
求抛物线解析式。
25．（8分）小王在超市用24元钱买了某种品牌的牛奶若干盒，过一段时间再去该超市，发现这种牛奶进行让利销售，每盒让利0.4元，他同样花24元钱，比上次多买2盒，求他第一次买了多少盒这种牛奶？
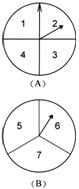26．（8分）甲乙两人在玩转盘游戏时，把转盘A、B分别分成4等份、3等份，并在每一份内标上数字，如图所示. 游戏规定，转动两个转盘停止后，指针所指的两个数字之和为奇数时，甲获胜；为偶数时，乙获胜．
（1）用列表法（或画树状图）求甲获胜的概率；
（2）你认为这个游戏规则对双方公平吗？请简要说明理由.
27．（13分）用一块边长为60cm的正方形薄钢片制作一个长方体盒子：
(1)如果要做成一个没有盖的长方体盒子，可先在薄钢片的四个角上截去四个相同的小正方形(如图1)，然后把四边折合起来(如图2)。若做成的盒子底面积为900
，求小正方形的边长。
(2)如果要做成一个有盖的长方体盒子，其制作方案要求同时符合下列两个条件：
①必须在薄钢片的四个角各截去一个四边形(其余部分不能裁截)；
②折合后薄钢片既无空隙、又不重叠地围成各盒面。
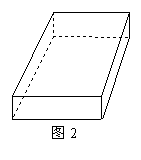
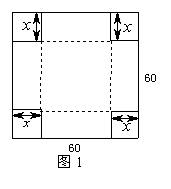请你画出符合上述制作方案的一种草图(不必说明画法与根据)；并求当底面积为800时，该盒子的高。
28．（13分）施工队要修建一个横断面为抛物线的公路隧道，其高度为6米，宽度OM为
12米.现以O点为原点，OM所在直线为X轴建立直角坐标系（如图所示）.
（1）直接写出点M及抛物线顶点P的坐标；
（2）求出这条抛物线的函数解析式；
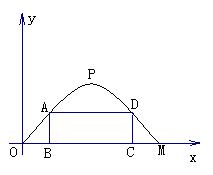（3）施工队计划在隧道门口搭建一个矩形“脚手架”CDAB，使A、D点在抛物线上，B、C点在地面OM上．为了筹备材料，需求出“脚手架”三根木杆AB、AD、DC的长度之和的最大值是多少？请你帮施工队计算一下.