初三数学总复习1
一、选择题（每题4分，共40分）
1.分解因式a-ab2的结果是( )
A.a(1+b)(1-b) B.a(1+b)2 C.a(1-b)2 D.(1-b)(1+b)
2.函数
自变量x的取值范围是( )
A.x≤
B.x≥
C.x≥
D.x≤
3、函数y=
（k≠0）的图象过点（2，-2），则此函数的图象在直角坐标系中的
A、第一、三象限 B、第三、四象限
C、第二、三象限 D、第二、四象限
4、一件衣服标价132元，若以9折降价出售，仍可获利10%，则这件衣服的进价是
A、106元 B、105元 C、118元 D、108元
5、方程x2 = 2x的解是
A、x=2 B、x1=
，x2= 0 C、x1=2，x2=0 D、x = 0
6、不等式组
的解集是（ ）．
(A)
(B)
(C)
(D)
7、今年2月3日我县最低气温为-6℃，最高气温为7℃，那么这一天最高气温比最低气温高 ( )
A．7℃ B．13℃ C．1℃ D．-13℃
8、25的平方根是 ( )
A．5 B．-5 C．±5 D．±
9、某同学为了解扬州火车站今年“春运”期间每天乘车人数，随机抽查了其中5天的乘车人数。所抽查的这5天中每天的乘车人数是这个问题的（ ）．
A．总体 B．个体 C．样本 D．样本容量
10、关于x的方程
有实数根，则K的取值范围是（ ）．
A．
B．
C．
D．
二、细心填一填（每空5分，共20分）
11、化简
得（
）
12、
的相反数是 ，
的绝对值是 ，
的倒数是 ．
13、小明五次测试成绩如下:91、89、88、90、92，则这五次测试成绩的平均数是 ，方差是
14、写出一个图象经过点(-1,-1),且不经过第一象限的函数表达_____________。
三、（15、16每题8分，17、18每题9分，20、21每题10分，共54分）
15、计算：(
)0+(
)-1-
--1
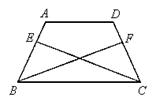16、已知：如图，在梯形ABCD中，AD∥BC，AB＝DC，点E、F分别在AB、DC上，且BE＝2EA，CF＝2FD。 求证：∠BEC＝∠CFB
17、解方程方程：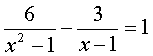
18、如图，点E是正方形ABCD的边CD上一点，点F是CB的延长线上一点，且EA⊥AF.
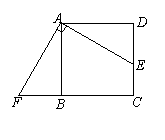求证：DE=BF.
19、有一块三角形的地，现要平均分给四农户种植（即四等分三角形面积）.请你在图上作出分法.（不写作法，保留作图痕迹）
 |
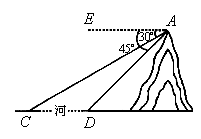20、如图，河旁有一座小山，从山顶A处测得河对岸点C的俯角为30°，测得岸边点D的俯角为45°，又知河宽CD为50米。现需从山顶A到河对岸点C拉一条笔直的缆绳AC，求缆绳AC的长（答案可带根号）。
四、本题12分。
21、若家用电冰箱冷若反比例函数
与一次函数
的图象都经过点A（
，2）
（1）求点A的坐标；
（2）求一次函数的解析式；
（3）设O为坐标原点，若两个函数图像的另一个交点为B，求△AOB的面积。
五、本题12分。
22、在“创优”活动中，我市某校开展收集废电池的活动，该校初二（1）班为了估计四月份收集电池的个数，随机抽取了该月某7天收集废旧电池的个数，数据如下：（单位：个）：48，51，53，47，49，50，52。求这七天该班收集废旧电池个数的平均数，并估计四月份（30天计）该班收集废旧电池的个数。
六、本题12分
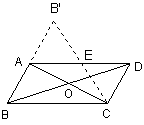
23、如图，在□ABCD的纸片中，AC⊥AB，AC与BD相交于O，将△ABC沿对角线AC翻转180°，得△ABC.
（1）求证：以A、C、D、B’为顶点的四边形是矩形；
（2）若四边形ABCD的面积S＝12cm. 求翻转后纸片重叠部分的面积，即S△ACE.
 |