初三中考复习数学综合测试卷
（满分130分）
一、细心填一填(3′×13=39′)
1.如图所示,AD⊥BC,DE⊥AB,DF⊥AC,D、E、F是垂足,BD=CD, 那么图中的全等三角形有________对.
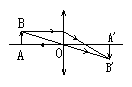
2.如图所示,已知当物体AB距凸透镜为2倍焦距,即AO=2f时,成倒立的等大的像A′B′.则像距OA′与f的关系为 .
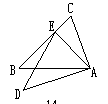
3.如图所示,把△ABC绕点A按逆时针旋转就得△ADE,则∠C=______。
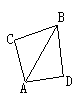
4.如图所示,在△ABC和△ABD中,∠C=∠D=90°,要使△ABC≌△ABD, 还需增加一个条件是__________.
5.将长度为20cm的铁丝折成三边长均为整数的三角形,那么, 不全等的三角形的个数为__________.
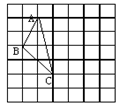
6．如图、在正方形网格上有一个ΔABC，①、作一个与它全等的三角形。②、如每一个小正方形的边长为1，则ΔABC的面积是：
7．抛物线
在
轴上截得的线段长度是
．
8．已知抛物线
与
轴交于点A，与轴的正半轴交于B、C两点，且BC=2，S△ABC=3，则
= ，
= ．
9．把二次函数
配方成顶点式为
。
10． 某人忘记了电话号码的最后一个数字，因而他随意地拨号，假设拨过了的号码不再重复，试求下列事件的概率：
（1）第3次拨号才接通电话； ；（2）拨号不超过3次而接通电话.
二、精心选一选(3′×10=30′)
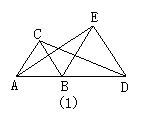
11.如图1所示,△ABC与△BDE都是等边三角形,AB<BD,若△ABC不动,将
△BDE 绕B点旋转,则旋转过程中,AE与CD的大小关系为( )
A.AE=CD B.AE>CD C.AE<CD D.无法确定
12.观察下列图形,并阅读图形下面的相关文字,如图所示:
两条直线相交,三条直线相交,四条直线相交,最多有一个交点,最多有三个交点;最多有6个交点,像这样,10条直线相交,最多交点的个数是( )
A.40个 B.45个C.50个 D.55个
13.下列条件中,不能使两个三角形全等的条件是( )
A.两边一角对应相等; B.两角一边对应相等
C.三边对应相等; D.两边和它们的夹角对应相等
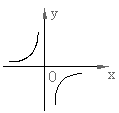14． 求作点P，使P到三角形三边的距离相等的方法是（ ）
A. 作两边的中垂线的交点 B. 作两边上的高线的交点
C. 作两边上的中线的交点 D. 作两角平分线的交点
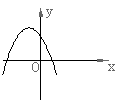
15．已知反比例函数
的图象如右图所示，则二次函数
的图象大致为（ ）
|
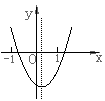
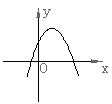
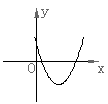
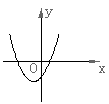16．二次函数
的图象如图所示，则 
，
，
，
这四个式子中，值为正数的有（ ）
A．4个 B．3个 C．2个 D．1个
17．函数
的图象与轴有交点，则
的取值范围是（ ）
A．
B．
C．
D．
18．直角坐标平面上将二次函数y＝-2(x－1)2－2的图象向左平移１个单位，再向上平移１个单位，则其顶点为（ ）
A.(0，0) B.(1，－2) C.(0，－1) D.(－2，1)
19．已知五个数2，3，1，5，4，那么它们的（ ）
（A）方差为
（B）方差为4 （C）平均数为3 （D）平均数为5
20．随机事件发生的概率是( )
A、0 B、0到1之间 C、1 D、无法确定
三、耐心解一解
22．(5′)已知：线段a，b求作：⊿ABC，使AB=AC，BC=a ，高AD=b
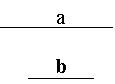
23．(9′)为了调查淮安市今年有多少名考生参加中考，小华从全市所有家庭中随机抽查了200个家庭，发现其中10个家庭有子女参加中考．
⑴本次抽查的200个家庭中，有子女参加中考的家庭的频率是多少？
⑵如果你随机调查一个家庭，估计该家庭有子女参加中考的概率是多少？
⑶已知淮安市约有1.3×106个家庭，假设有子女参加中考的每个家庭中只有一名考生，请你估计今年全市有多少名考生参加中考?
24.(8′)如图所示,AB=AE,∠ABC=∠AED,BC=ED,点F是CD的中点.
(1)求证:AF⊥CD;
(2)在连结BE后,你还能得出什么新结论?请写出三个(不要求证明).
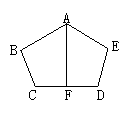
25.(8′)如图所示,已知AB为⊙O的直径,C、D为圆上两点,CE⊥AB,DF⊥AB, 垂足分别为E、F,且
,求证:CE=DF.
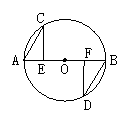
26．(8′)已知△ABC中，∠C = 90°，沿过B的一条直线BE折叠这个三角形，使点C与AB边上的一点D重合。如图所示。要使D恰为AB的中点，还应添加一个什么条件？（请你写出三种不同的添加条件）选择（1）中的某一个添加条件作为题目的补充条件，试说明其能使D为AB中点的理由。
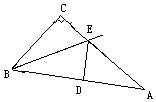解：（1）添加条件：①_____________；
②_______________；③________。
（2）说明：
|
|
|
，二次函数
。
(1)
根据表中给出的的值，计算对应的函数值
、
，并填在表格中：
|
| -3 | -2 | -1 | 0 | 1 | 2 | 3 |
|
| |||||||
|
|
(2)
观察第(1)问表中有关数据，证明如下结论：在实数范围内，对于的同一个值，这两个函数所对应的函数值≤均成立；
27．(12′)如图，在一块三角形区域ABC中，∠C=90°，边AC=8，BC=6，现要在△ABC内建造一个矩形水池DEFG，如图的设计方案是使DE在AB上。
⑴求△ABC中AB边上的高h;
⑵设DG=x,当x取何值时，水池DEFG的面积最大？
⑶实际施工时，发现在AB上距B点1.85的M处有一棵大树，问：这棵大树是否位于最大矩形水池的边上？如果在，为保护大树，请设计出另外的方案，使三角形区域中欲建的最大矩形水池能避开大树。
 |