初中毕业会考数学试卷(新课程)
考生注意：本试卷共十道大题，其中正卷八道题，满分100分；另附加题二道题，共20分，时量120分钟．
一、填空题（本题共12个小题，每小题2分，共24分）
1．函数
中自变量
的取值范围是 ．
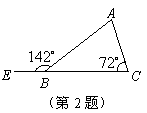
2．如右图，已知
，
，则
，
．
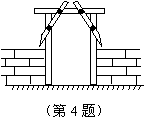3．永州市现共有11个县（区），总地域面积约亩，用科学记数法（保留三个有效数字）表示这一数据为 亩．
4．工人师傅在安装木制门框时，为防止变形常常像图中所示，钉上两条斜拉的木条，这样做的原理是根据三角形的 性．
5．不等式组
的解集是 ．
6． 的平行四边形是菱形（填一个合适的条件）．
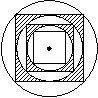
7．如图所示是 体的展开图．
8．在建设社会主义新农村活动中，张村、李村为合理利用资源，优化环境，兴建了一批沼气池，设张村已建沼气池个，李村所建沼气池的数目是张村的2倍少1个，则李村所建沼气池数目为 个（用代数式表示）．
9．如图为九嶷山风景区的几个景点的平面图，以舜帝陵为坐标原点，建立平面直角坐标系，则玉王宫岩所在位置的坐标为 ．
 |
10．如图所示，在等腰三角形
中，
，
，那么底边上的高
cm．
11．在10000株樟树苗中，任意测量20株的苗高，这个问题中，样本容量是 ．
12．如右图所示为农村一古老的捣碎器，已知支撑柱
的高为0.3米，踏板
长为1.6米，支撑点
到踏脚
的距离为0.6米，现在踏脚着地，则捣头点
上升了 米．
二、选择题：（每题只有一个正确选项，请将正确选项的代号填入下表，本题共8个小题，每小题3分，共24分）
13．
在
中，无理数的个数是（ ）
A．1 B．2 C． 3 D．4
14．在下列二次根式中，与
是同类二次根式的是（ ）
A．
B．
C．
D．
15．在下列图形中，既是中心对称又是轴对称的图形是（ ）
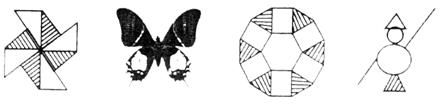
（纸风车） （中国国蝶） （美丽的地板） （稻草人）
A． B． C． D．
16．已知
，下列四个不等式中，不正确的是（ ）
A．
B．
C．
D．
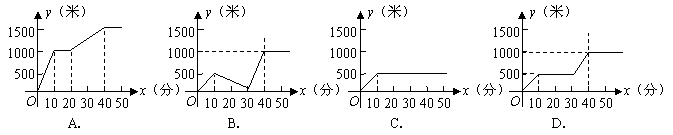17．小慧今天到学校参加初中毕业会考，从家里出发走10分钟到离家500米的地方吃早餐，吃早餐用了20分钟；再用10分钟赶到离家1000米的学校参加考试．下列图象中，能反映这一过程的是（ ）
18．在2，3，4，5，五个数据中，平均数是4，那么这组数据的方差是（ ）
A．2 B．10 C．
D．
19．某市电视台在今年5月举办的“开心就唱”歌手大赛活动中，号召观众发短信为参赛者投支持票，投票短信每1万条为1组，每组抽出1个一等奖，3个二等奖，6个三等奖．张艺同学发了1条短信，她的获奖概率是（ ）
A．
B．
C．
D．
20．如图，在半径为
的圆内作一个内接正方形，然后作这个正方形的内切圆，又在这个内切圆中作内接正方形，依此作到第
个内切圆，它的半径是（ ）
A．
B．
C．
D．
三、（本题含两个小题，每小题6分，共12分）
21．计算：
．
22．化简求值：
，其中
，
．
四、（本题满分6分）
23．请画出已知图形（如图所示）关于直线
的对称图形．（保留作图痕迹，不写画法）
 |
五、（本题满分8分）
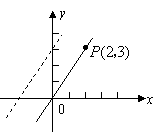
24．已知正比例函数
经过点
．（如图所示）
（1）求这个正比例函数的解析式．
（2）该直线向上平移3个单位，求平移后所得直线的解析式．
 |
六、（本题满分8分）
25．2006年“五一”长假期间，永州市政府在阳明山风景区举办了“阳明山‘和’文化节”，参加人数多达26000人，7天内参加人员按地域来源分类统计的结果是：
一．永州市内人数占50%；
二．湖南省内，永州市外的来客占25%；
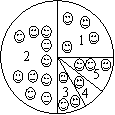三．中国内地，湖南省外的来客占12%；
四．港、澳、台三地同胞占8%；
五．国外游客占5%．
扇形统计图如右图所示：
（一）把各地域代号与扇形区域代号的对应关系，
用线段连接起来：
一
二 三 四 五
1 2 3 4 5
（二）求参加“阳明山‘和’文化节”活动的港、澳、台同胞的人数．
七、（本题满分8分）
26．李大伯承包了一片荒山，在山上种植了一部分优质油桃，今年已进入第三年收获期．今年收获油桃6912千克，已知李大伯第一年收获的油桃重量为4800千克．试求去年和今年两年油桃产量的年平均增长率，照此增长率，预计明年油桃的产量为多少千克？
八、（本题满分10分）
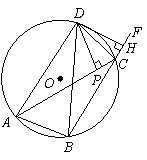
27．如图
的内接
中，外角
的角平分线与相交于点，
，垂足为，
，垂足为
．
问：（1）
与
是否相等？为什么？
（2）图中有哪几组相等的线段？
（3）当满足什么条件时，
，为什么？
 |
（附加题）九、（本题满分10分）
28．已知抛物线
经过点
．
（1）求抛物线的解析式．
（2）设抛物线顶点为
，与
轴交点为．求
的值．
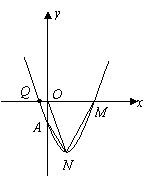（3）设抛物线与轴的另一个交点为
，求四边形
的面积．
（附加题）十、（本题满分10分）
29．如图，以
为圆心的两个同心圆中，大圆的直径
交小圆于
两点，大圆的弦切小圆于点
，过点作直线
，垂足为，交大圆于
两点．
（1）试判断线段
与
的大小关系，并说明理由．
（2）求证：
．
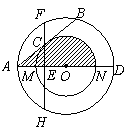（3）若
是方程
的两根（
），求图中阴影部分图形的周长．
初中毕业会考试卷参考答案及评分标准
数 学（新课标）
一、填空题（12个小题，每题2分，共24分）
1．
2．
3．
4．稳定
5．
或
6．对角线互相垂直或（一组）邻边相等
7．六棱锥 8．
9．
10．6 11．20 12．0.8
二、选择题（8个小题，每题3分，共24分）
| 题号 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 答案 | B | C | C | B | D | A | B | A |
三、计算（共2题，每题6分，共12分）
21．解：原式=
···················································································· 3分
．····································································· 6分
22．化简求值：
解：原式
··································································· 2分
．······································································································· 3分
当
时，
······················································································· 4分
．························································································· 6分
四、作图题（共6分）
23．（画出了轴对称图形6分，无作图痕迹扣2分）
 |
五、（共8分）
24．（1）解：由函数经过点
，可得：
，解析式为：
．······· 4分
（2）解：直线向上平移3个单位后，得到的解析式为：
．············· 8分
六、（本题共8分）
25．（1）一 二 三 四 五
1 2 3 4 5
（2）解：
（人）··········································································· 4分
答：参加“和”节的港、澳、台同胞的人数为2080人．················································ 8分
七、（本题共8分）
26．解：设油桃今年和去年的年平均增长率为，依题意得：······································· 1分
．································································································· 3分
解方程得：
或
（舍去负根）得
．··································· 5分
预计明年的产量为：
（千克）．············································ 7分
答：年平均增长率为20%，照此增长率，预计明年的产量为8294.4千克．···················· 8分
八、（本题共10分）
27．（1）答：相等．······································································································ 1分
因为
为的角平分线（已知），
．
，
．
．································································································· 3分
（2）
．（写出一组得1分）··················· 7分
（3）
且
时，，······································· 9分
因为
为直角，所以
为直角，为的角平分线，
，所以．···················································· 10分
附加题 九、（本题共10分）
28．（1）解方程组
得
，
．·················································································· 3分
（2）顶点
．················································· 6分
（3）在
中，令
得
，
，
令
得
或
，
．············································································ 8分
四边形
（面积单位）···················································· 10分
十、（本题满分10分）
29．（1）相等．············································································································· 1分
连结
，则
，故
．····································································· 3分
（2）由
，得
，······································· 4分
又由
，得
．····························································· 5分
．································································································ 6分
（3）解方程得：
，
，··························································· 7分
，
，
在
中，
，
，
．
在
中，
，
，
，
弧
长
，
，······· 9分
阴影部分周长
．················································ 10分