初中毕业暨高中阶段招生考试数学试卷(A)
注意事项:
1.全卷共计150分,考试时间120分钟.考生在答题前务必将毕业学校、报考学校、姓名、准考证号、座位号填写在试卷的相应位置上.
2.答题时请用同一颜色(蓝色或黑色)的钢笔、碳素笔或圆珠笔将答案直接写在考试卷上,要求字迹工整,卷面整洁.
3.不得另加附页,附页上答题不记分.
一、选择题(本题共12个小题,每小题4分,共计48分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.已知相切两圆的半径是一元二次方程![]() 的两个根,则这两个圆的圆心距是( ).
的两个根,则这两个圆的圆心距是( ).
A.7 B.1或7 C.1 D.6
2.为了估计湖中有多少条鱼,先从湖中捕捉50条鱼做记号,然后放回湖里,经过一段时间,等带记号的鱼完全混于鱼群中之后,再捕捞第二次鱼共200条,有10条做了记号,则估计湖里有( )条鱼.
A.400条 B.500条 C.800条 D.1000条
3.某地2004年外贸收入为2.5亿元,2006年外贸收入达到了4亿元,若平均每年的增长率为![]() ,则可以列出方程为( ).
,则可以列出方程为( ).
 A.
A.![]() B.
B.![]()
C.![]() D.
D.![]()
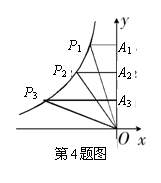
4.如图,![]() ,
,![]() ,
,![]() 是双曲线上的三点,过这三点分别作
是双曲线上的三点,过这三点分别作![]() 轴的垂线,得到三个三角形
轴的垂线,得到三个三角形![]() ,
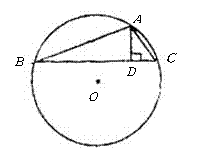
,![]() ,
,![]() ,设它们的面积分别是
,设它们的面积分别是![]() ,
,![]() ,
,![]() 则( ).
则( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.在![]() 中,
中,![]() ,下列各式中正确的是( ).
,下列各式中正确的是( ).
 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.书包里有数学书3本、英语书2本、语文书5本,从中任意抽取一本,则是数学书的概率是( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
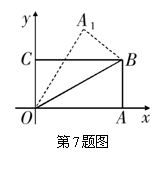
7.如图,在直角坐标系中,将矩形![]() 沿
沿![]() 对折,使点
对折,使点![]() 落在
落在![]() 处,已知
处,已知![]() ,
,![]() ,则点
,则点![]() 的坐标是( ).
的坐标是( ).
A. B.
B.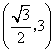 C.
C.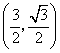 D.
D.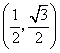
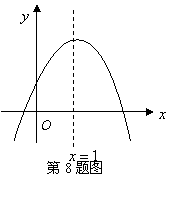 8.已知二次函数
8.已知二次函数![]() 的图象如图所示,对称轴是
的图象如图所示,对称轴是![]() ,则下列结论中正确的是( ).
,则下列结论中正确的是( ).
A.![]() B.
B.![]()
C.![]() D.
D.![]()
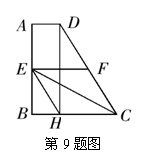 9.如图:在直角梯形
9.如图:在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为梯形的中位线,
为梯形的中位线,![]() 为梯形的高,则下列结论:①
为梯形的高,则下列结论:①![]() ,②四边形
,②四边形![]() 为菱形,③
为菱形,③![]() ,④以
,④以![]() 为直径的圆与
为直径的圆与![]() 相切于点
相切于点![]() ,其中正确结论的个数为( ).
,其中正确结论的个数为( ).
A.4 B.3 C.2 D.1
10.已知![]() 的图象是抛物线,若抛物线不动,把
的图象是抛物线,若抛物线不动,把![]() 轴,
轴,![]() 轴分别向上、向右平移2个单位,那么在新坐标系下抛物线的解析式是( ).
轴分别向上、向右平移2个单位,那么在新坐标系下抛物线的解析式是( ).
A.![]() B.
B.![]()
C.![]() D.
D.![]()
11.若圆锥经过轴的截面是一个正三角形,则它的侧面积与底面积之比是( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.在![]() 中,弦
中,弦![]() 与直径
与直径![]() 相交于点
相交于点![]() ,夹角为
,夹角为![]() ,且分直径为
,且分直径为![]() 两部分,
两部分,![]() 厘米,则弦
厘米,则弦![]() 的长为( )厘米.
的长为( )厘米.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(本题共8个小题,每小题4分,共32分,请把答案填在题中的横线上)
13.在函数![]() 中,自变量
中,自变量![]() 的取值范围是 .
的取值范围是 .
 14.已知
14.已知![]() 是方程
是方程![]() 的两根,则
的两根,则![]() 的值是 .
的值是 .
15.如图,是正方体的平面展开图,每个面上标有一个汉字组成的三个词,分别是兰州人引以自豪的“三个一”(一本书,一条河,一碗面),在正方体上与“读”字相对的面上的字是 .
16.在实数范围内定义一种运算“![]() ”,其规则为
”,其规则为![]() ,根据这个规则,方程
,根据这个规则,方程![]() 的解为 .
的解为 .
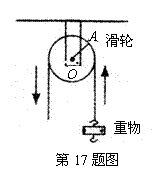 17.一个滑轮起重装置如图所示,滑轮的半径是10cm,当重物上升10cm时,滑轮的一条半径
17.一个滑轮起重装置如图所示,滑轮的半径是10cm,当重物上升10cm时,滑轮的一条半径![]() 绕轴心
绕轴心![]() 按逆时针方向旋转的角度约为 .(假设绳索与滑轮之间没有滑动,
按逆时针方向旋转的角度约为 .(假设绳索与滑轮之间没有滑动,![]() 取
取![]() ,结果精确到
,结果精确到![]() )
)
18.开口向下的抛物线![]() 的对称轴经过点
的对称轴经过点![]() ,则
,则![]() .
.
19.已知等腰![]() 内接于半径为5的
内接于半径为5的![]() ,如果底边
,如果底边![]() 的长为6,则底角的正切值为 .
的长为6,则底角的正切值为 .
20.请选择一组你喜欢的![]() 的值,使二次函数
的值,使二次函数![]() 的图象同时满足下列条件:①开口向下,②当
的图象同时满足下列条件:①开口向下,②当![]() 时,
时,![]() 随
随![]() 的增大而增大;当
的增大而增大;当![]() 时,
时,![]() 随
随![]() 的增大而减小.这样的二次函数的解析式可以是 .
的增大而减小.这样的二次函数的解析式可以是 .
三、解答题(本大题共10道题,共计70分,解答时应写出必要的文字说明、证明过程或演算步骤)
21.(本题满分6分)
随机抽查某城市30天的空气状况统计如下:
| 污染指数( | 40 | 60 | 90 | 110 | 120 |
| 天数( | 3 | 3 | 9 | 10 | 5 |
其中,![]() 时,空气质量为优:
时,空气质量为优:![]() 时,空气质量为良;
时,空气质量为良;![]() 时,空气质量为轻微污染.
时,空气质量为轻微污染.
(1)请用扇形统计图表示这30天中空气质量的优、良、轻微污染的分布情况;
(2)估计该城市一年(365天)中有多少天空气质量达到良以上.
22.(本题满分6分)
小明想测量校园内一棵不可攀的树的高度.由于无法直接度量![]() 两点间的距离,请你用学过的数学知识按以下要求设计一种测量方案.
两点间的距离,请你用学过的数学知识按以下要求设计一种测量方案.
(1)画出测量图案;
(2)写出测量步骤(测量数据用字母表示);
(3)计算![]() 间的距离(写出求解或推理过程,结果用字母表示).
间的距离(写出求解或推理过程,结果用字母表示).
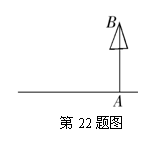 |
23.(本题满分6分)
如图,![]() 是
是![]() 的直径,
的直径,![]() 交
交![]() 的中点于
的中点于![]() ,
,![]()
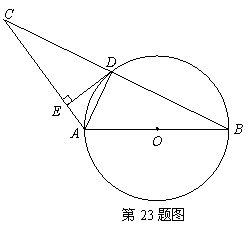 (1)求证:
(1)求证:![]() ;
;
(2)求证:![]() 是
是![]() 的切线.
的切线.
24.(本题满分6分)
如图所示,在![]() 中,
中,![]() 分别是
分别是![]() 和
和![]() 上的一点,
上的一点,![]() 与
与![]() 交于点
交于点![]() ,给出下列四个条件:①
,给出下列四个条件:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.
(1)上述四个条件中,哪两个条件可以判定![]() 是等腰三角形(用序号写出所有的情形);
是等腰三角形(用序号写出所有的情形);
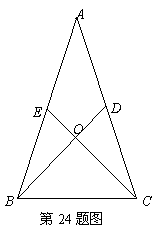 (2)选择(1)小题中的一种情形,证明
(2)选择(1)小题中的一种情形,证明![]() 是等腰三角形.
是等腰三角形.
25.(本题满分6分)
有两个可以自由转动的均匀转盘![]() ,分别被分成4等份,3等份,并在每份内均标有数字,如图所示,丁洋和王倩同学用这两个转盘做游戏,游戏规则如下:
,分别被分成4等份,3等份,并在每份内均标有数字,如图所示,丁洋和王倩同学用这两个转盘做游戏,游戏规则如下:
①分别转动转盘![]() 和
和![]() ;②两个转盘停止后,将两个指针所指份内的数字相加(如果指针恰好停在等分线上,那么重转一次,直到指针指向某一份为止;③如果和为0,丁洋获胜,否则王倩获胜.
;②两个转盘停止后,将两个指针所指份内的数字相加(如果指针恰好停在等分线上,那么重转一次,直到指针指向某一份为止;③如果和为0,丁洋获胜,否则王倩获胜.
(1)用列表法(或树状图)求丁洋获胜的概率;
(2)你认为这个游戏对双方公平吗?请说明理由.
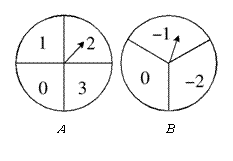 |
26.(本题满分7分)
如图所示,有一座抛物线形拱桥,桥下面在正常水位![]() 时,宽
时,宽![]() ,水位上升
,水位上升![]() 就达到警戒线
就达到警戒线![]() ,这时水面宽度为
,这时水面宽度为![]() .
.
(1)在如图的坐标系中求抛物线的解析式;
 (2)若洪水到来时,水位以每小时
(2)若洪水到来时,水位以每小时![]() 的速度上升,从警戒线开始,再持续多少小时才能到达拱桥顶?
的速度上升,从警戒线开始,再持续多少小时才能到达拱桥顶?
27.(本题满分8分)
已知一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象相交,其中一个交点的纵坐标为6.
的图象相交,其中一个交点的纵坐标为6.
(1)求两个函数的解析式;
(2)结合图象求出![]() 时,
时,![]() 的取值范围.
的取值范围.
28.(本题满分8分)
在![]() 的内接
的内接![]() 中,
中,![]() ,
,![]() ,垂足为
,垂足为![]() ,且
,且![]() ,设
,设![]() 的半径为
的半径为![]() ,
,![]() 的长为
的长为![]() .
.
(1)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)当![]() 的长等于多少时,
的长等于多少时,![]() 的面积最大,并求出
的面积最大,并求出![]() 的最大面积.
的最大面积.
29.(本题满分8分)
 广场上有一个充满氢气的气球
广场上有一个充满氢气的气球![]() ,被广告条拽着悬在空中,甲乙二人分别站在
,被广告条拽着悬在空中,甲乙二人分别站在![]() 处,他们看气球的仰角分别是
处,他们看气球的仰角分别是![]() ,
,![]() ,
,![]() 点与
点与![]() 点的高度差
点的高度差![]() 为1米,水平距离
为1米,水平距离![]() 为5米,
为5米,![]() 的高度为
的高度为![]() 米,请问此气球有多高?(结果保留到
米,请问此气球有多高?(结果保留到![]() 米)
米)
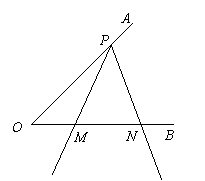
30.如图,已知![]() 为
为![]() 的边
的边![]() 上的一点,以
上的一点,以![]() 为顶点的
为顶点的![]() 的两边分别交射线
的两边分别交射线![]() 于
于![]() 两点,且
两点,且![]() (
(![]() 为锐角).当
为锐角).当![]() 以点
以点![]() 为旋转中心,
为旋转中心,![]() 边与
边与![]() 重合的位置开始,按逆时针方向旋转(
重合的位置开始,按逆时针方向旋转(![]() 保持不变)时,
保持不变)时,![]() 两点在射线
两点在射线![]() 上同时以不同的速度向右平行移动.设
上同时以不同的速度向右平行移动.设![]() ,
,![]() (
(![]() ),
),![]() 的面积为
的面积为![]() .若
.若![]() .
.
(1)当![]() 旋转
旋转![]() (即
(即![]() )时,求点
)时,求点![]() 移动的距离;
移动的距离;
(2)求证:![]() ;
;
(3)写出![]() 与
与![]() 之间的关系式;
之间的关系式;
 (4)试写出
(4)试写出![]() 随
随![]() 变化的函数关系式,并确定
变化的函数关系式,并确定![]() 的取值范围.
的取值范围.
数学参考答案(A)
注:对另解情况均酌情给分.
一、选择题:(本大题共12个小题,每小题4分,共48分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | D | A | D | C | C | A | D | B | B | D | B |
二、填空题:(本大题共有8个小题,每小题4分,共32分)
13.![]() ; 14.
; 14.![]() ; 15.面; 16.
; 15.面; 16.![]() 或
或![]() ; 17.
; 17.![]() ;
;
18.![]() ; 19.
; 19.![]() 或
或![]() ; 20.答案不唯一,只要满足对称轴是
; 20.答案不唯一,只要满足对称轴是![]() ,
,![]() .
.
三、解答题:(本大题共有10道题,共计70分)
21.本题满分6分
解:(1)设![]() 天中空气质量分别为优、良、轻微污染的扇形图的圆心角依次为
天中空气质量分别为优、良、轻微污染的扇形图的圆心角依次为![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]() ··································································································· 3分
··································································································· 3分
扇形统计图为:
···························································· 5分
(2)一年中空气质量达到良以上的天数约为:
![]() (天)·············································································· 6分
(天)·············································································· 6分
 22.本题满分6分
22.本题满分6分
(1)答案不唯一,提供一种方案:
测量平面图如图:
················································· 2分
(2)测量出![]() ································································ 4分
································································ 4分
(3)![]() .····························································································· 6分
.····························································································· 6分
23.本题满分6分
解:(1)![]() 是
是![]() 的半径,
的半径,
![]() ,········································································································· 1分
,········································································································· 1分
又![]() ,
,![]() ,
,![]() ,······························································ 2分
,······························································ 2分
![]() ,
,
![]() ····································································································· 3分
····································································································· 3分
(2)连接![]() ,
,
![]() ,
,![]() ,
,
![]() ,············································································································· 5分
,············································································································· 5分
又![]() ,
,
![]() ,所以
,所以![]() 是
是![]() 的切线·········································································· 6分
的切线·········································································· 6分
24.本题满分6分
(1)①③,①④,②③,②④
每对一组得![]() 分·············································································································· 4分
分·············································································································· 4分
(2)证明:略·············································································································· 6分
25.本题满分6分
解:(1)每次游戏可能出现的所有结果列表如下:
| 转盘 转盘 的数字 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
根据表格,共有![]() 种可能的结果,··············································································· 2分
种可能的结果,··············································································· 2分
其中和为![]() 的有三种:
的有三种:
![]() ,
,![]() ,
,![]()
![]() 丁洋获胜的概率为
丁洋获胜的概率为![]() ·········································· 4分
·········································· 4分
(2)这个游戏不公平
![]() 丁洋获胜的概率为
丁洋获胜的概率为![]() ,王倩获胜的概率为
,王倩获胜的概率为![]() ,
,![]() ,
,![]() 游戏对双方不公平
游戏对双方不公平
······························································· 6分
26.本题满分7分
解:(1)设所求抛物线的解析式为:![]() ································································ 1分
································································ 1分
设![]() 则
则![]() ························································································· 3分
························································································· 3分
![]() ,
,![]()
解得
![]() ··············································································································· 5分
··············································································································· 5分
(2)![]() ,
,![]() 小时
小时
所以再持续![]() 小时到达拱桥顶.····················································································· 7分
小时到达拱桥顶.····················································································· 7分
27.本题满分8分
解:(1)由已知设交点![]()
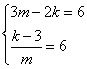 ··············································································································· 2分
··············································································································· 2分
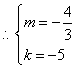 ·················································································································· 3分
·················································································································· 3分
![]() ,
,![]() ····························································································· 4分
····························································································· 4分
(2)由方程组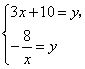 得
得![]() ,
,
![]() ,
,![]() ······································································································· 6分
······································································································· 6分
由图像可知当![]() 或
或![]() 时
时![]() ································································ 8分
································································ 8分
28.本题满分8分
解:(1)作直径![]() ,连接
,连接![]() ,则
,则![]() ························································· 1分
························································· 1分
![]() ,
,![]() ·············································································· 2分
·············································································· 2分
又![]() ,
,![]() ············································································· 3分
············································································· 3分
![]() 即
即![]() ··························································································· 4分
··························································································· 4分
![]() ········································································································· 5分
········································································································· 5分
当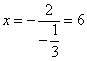 时,
时,![]() 最大为
最大为![]() .················································································ 7分
.················································································ 7分
![]() 的最大面积为
的最大面积为![]() .··························································································· 8分
.··························································································· 8分
29.本题满分8分
解:设![]() 米·········································································································· 1分
米·········································································································· 1分
![]() ,
,![]() ··········································································· 2分
··········································································· 2分
![]() ················································································································ 3分
················································································································ 3分
在![]() 中,
中,![]()
![]() ····································································································· 5分
····································································································· 5分
![]() ,
,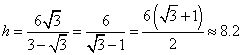 米········································ 6分
米········································ 6分
![]() 气球的高度为
气球的高度为![]() 米·················································· 8分
米·················································· 8分
30.本题满分9分
解:(1)![]() 且
且![]() 为锐角,
为锐角,![]() ,即
,即![]() ,·············· 1分
,·············· 1分
![]() 初始状态时,
初始状态时,![]() 为等边三角形,
为等边三角形,
![]() ,当
,当![]() 旋转到
旋转到![]() 时,点
时,点![]() 移动到
移动到![]() ,
,![]() ,
,
![]() ,
,![]() ,······························································· 2分
,······························································· 2分
在![]() 中,
中,![]() ,
,![]() ,
,
![]() 点
点![]() 移动的距离为
移动的距离为![]() ································································································· 3分
································································································· 3分
(2)在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,
![]() ,································································································· 4分
,································································································· 4分
(3)![]() ,
,![]() ,
,
过![]() 点作
点作![]() ,垂足为
,垂足为![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,
在![]() 中,
中,![]()
![]() ························ 5分
························ 5分
![]() ,即
,即![]() ········································································· 6分
········································································· 6分
(4)在![]() 中,
中,![]() 边上的高
边上的高![]() 为
为![]()
![]() ············································································· 8分
············································································· 8分
![]() ,
,![]() ,即
,即![]() ,
,
又![]() ,
,![]() 的取值范围是
的取值范围是![]() ;
;
![]() 是
是![]() 的正比例函数,且比例系数
的正比例函数,且比例系数![]() ,
,![]() ,即
,即![]()
···························································· 9分