初三数学第27章证明复习
一．知识体系表解
角平分线
基本概念
中线
用
高
推 三
中位线 （三角形的中位线平行于第三边，且等于第三边的一半）
理 角
三边关系定理 （任意两边这和（差）大于（小于）第三边）
的 形 性质 三角形按边分类
方
内角和定理（180º）
三角形按角分类
法
判定（S，S，S； S，A，S； A，S，A； A，A，S
研
全等三角形
直角三角形角形还有特殊的：H L ）
究
性质 （边、角、高、中线、角平分线、面积）
四边形 见背面
二．例题
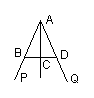
1． 已知，如图，AC平分∠PAQ，点B、D分别在边AP、AQ上，如果
添加一个条件，即可推出AB=AD，那么添加的条件可以是 。
A、BD⊥AC B、BC=DC C、∠ACB=∠ACD D、∠ABC=∠ADC
2．
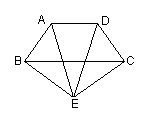如图，在等腰梯形ABCD中，AB=CD，AD//BC，E是
梯形外一点，且EA=ED。求证：EB=EC。
3．已知：△ABC中，AB=10，AC=6，则BC边上的中线的取值范围是 。
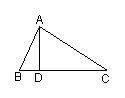
4．如图，在△ABC中，AD⊥BC于点D，∠B=2∠C。求证：AB+BD=DC。
 |
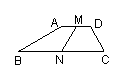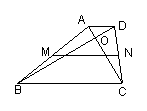
5．如图，在四边形ABCD中，AD//BC，M、N分别是BC、AD的中点，
∠B+∠C=90º，求证：MN =
。
 |
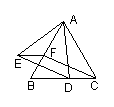
6．如图，在梯形ABCD中，AD//BC，AC⊥BD于点O，
MN是梯形的中位线，∠DBC=30º。求证：AC=MN。
 |
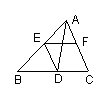
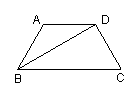
7．如图，△ABC是等边三角形，D、F分别是BC、AB边上的点，
且CD=BF，以AD为边作等边△ADE。求证：四边形CDEF为平行四边形。
 |
8．已知：在△ABC中，AD是∠BAC的平分线，DE//AC交AB于点E，
EF//BC交AC于点F。求证：AE=FC。
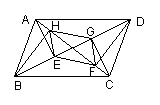
9．已知：如图，从 ABCD的各个项点，向对角线作垂线，
垂足依次为E、F、G、H。求证：四边形EFGH为平行四边形。
 |
10．已知：如图，在等腰梯形ABCD中，AD//BC，AD=AB，
BD⊥CD。求梯形各内角的度数。
 |
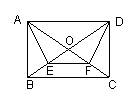11．已知：如图，在矩形ABCD中，对角线交于点O，E、F分别
是OB、OC的中点。求证：（1）AE=DF。（2）四边形AEFD为等腰
梯形。
 |
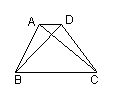12．如图，在在梯形ABCD中，AD//BC，AD=2，BC=8，BD=8，
AC=6，则它的面积为 。
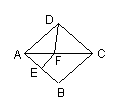13．如图，在菱形ABCD中，∠DAB=80º，EF垂直平分AB于E，
交AC于点F。求：∠CDF的度数。
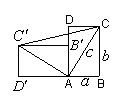14．一个直立的火柴盒在桌面上倒下，启迪人们发现了勾股定理的一种
新的证明方法。如图，火柴盒的一个侧面ABCD倒下到A
的位置，
连结
，设
，
，
，请利用四边形
的
面积说明勾股定理
成立。
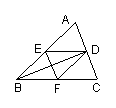15．如图，BD是△ABC的角平分线，EF是BD的垂直平分线。求证：四边形BFDE是菱形。