初三数学第二次模拟考试试卷

初三数学第二次模拟考试试卷

一、选择题（本大题共12小题，1—8题每题2分，9—12题每题3分，共28分。下列各题的

四个结论中，只有一个是正确的。请将正确的答案的字母代号填在下面的表格内。）

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案

一、选择题（本大题共12小题，1—8题每题2分，9—12每题3分，共28分）。下列各题的四个结论中只有一个是正确的，请将正确答案的字母代号填在下面表格内。

1．今年我市二月份某一天的最低气温为—5⁰C，最高气温为12⁰C，那么这一天的最高气温比最低气温高（　 ）

A．—18⁰C　　　　　　B．17⁰C　　　　　　　　C．18⁰C　　　　　　　 D．5⁰C

2．计算等于（　 ）

A．　　　　　　　　 B．　　　　　　　　 C．　　　　　　　 D．

3．若为锐角，则的值是（　 ）

A．　　　　　　　　　B．　　　　　　　　C．　　　　　　　　D．

4．函数 中，自变量的取值范围是（　　）

A．≥0　　　　　　　B．＞0且≠1　　　　C．＞0　　　　　　　D．≥0且≠1

5．已知的值是（　 ）

A．4　　　　　　　　 B．6　　　　　　　　　C．　　　　　　　　　D．

6．要判定“平行四边形ABCD是菱形”只要再加条件（　 ）

A．AB=CD　　　　　 B．AC=BD　　　　　　C．AB⊥BC　 　　　D．AC⊥BD

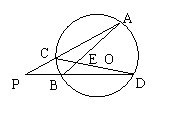
7．如图，⊙O的两条弦AB、CD相交于点E，AC与DB的

延长线交于点P，下列结论中成立的是（　 ）

A．CE·CD=BE·BA　　　　　　　　　　　　B．CE·AE=BE·DE

C．PC·CA=PB·BD　　　　　　　　　　　　D．PC·PA=PB·PD

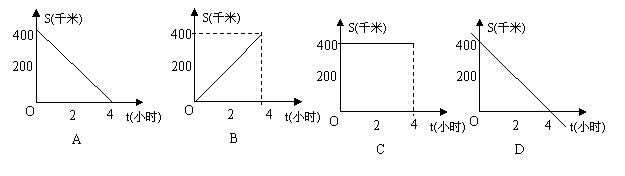
8．汽车由南通驶往相距400千米的杭州，如果汽车的平均速度是100千米/小时，那么汽车距杭州的路程S（千米）与行驶时间t（小时）的函数关系用图象表示为（　 ）

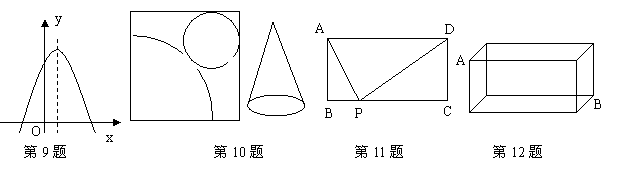
9．已知二次函数的图象如图所示，则不等式＞0的解集为（　）

A．＞　　　　　　　　　B．＞　　　　　　　　C．＜　　　　　　　　　 D．＜—

10．如图在正方形铁皮上剪下一个圆形和扇形，使之恰好围成一个圆锥的模型，设圆的半径为r，扇形的半径为R，则r与R之间的关系是（　 ）

A．R=4r　　　　　　　　　　　B．R=3r　　　　　　　　　　　C．R=r　　　　　　　　　　D．R=2r

11．如图矩形ABCD中，AD=a，AB=b，要使BC边上至少存在一个P，使△ABP、△APD、△CDP两两相似，则a、b间的关系一定满足（　 ）

A．a≥2b　　　　　　　　　　 B．a≥b　　　　　　　　　 C．a≥b　　　　　　　　　　　 D．a≥b

12．如图是一块长、宽、高分别是6cm、4cm和3cm的长方形木块，一只只会爬行的甲虫要从长方体木块的一个顶点A处，沿着长方体的表面爬到长方体上和点A相对的顶点B处吃食物，那么它需要爬行的最短路径长是（　 ）

A．cm　　　　 B．cm　　　　　C．cm　　　　　D．cm

二、填空（本大题共6小题，每题3分，共18分）

13．写出一个3到4之间的无理数________。

14．分解因式：a²+a—b²—b=____________________。

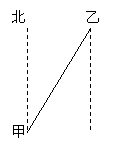
15．如图，在甲、乙两地之间修一条笔直的公路，

从甲地测得乙地在北偏东48⁰的方向，则从乙地

第15题

观察甲地的方向应在_______________度的方向。

16．抛物线开口向下，且经过原点，则的值为_________。

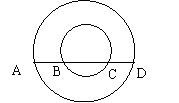17．如图两个同心圆的半径分别是2和4，大圆的弦AD交小圆于

B、C两点，且AB=BC=CD，则AB的长度等于__________。

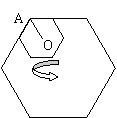
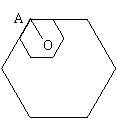
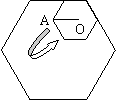
18．如图，小正六边形的边长是1，大正六边形的边长是2。

第17题

A是小正六边形的一个顶点，若小正六边形沿大正六边形内侧

滚动一周，回到原来的位置，则OA旋转过的角度为______度。

　　　　　　　　　　　　　　　　　　　

三、解答题（本大题共10题，共84分）

19．（本题共10分）

（1）计算　　（2）化简

＜5x

20．（本题6分）解不等式组

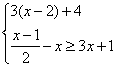
21．已知如图Rt△AOB的顶点A（a，b）是一次函数的图象与反比例函数的图象在第一象限的交点且S_△AOB=3。

（1）求一次函数与反比例函数的解析式。　（2）求A点的坐标。

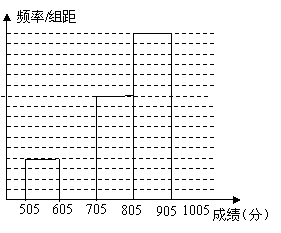22．（本题7分）为了让学生了解环保知识增强环保意识，我校举行了一次“环保知识竞赛”，共有900名学生参加了这次竞赛。为了解本次竞赛成绩情况，从中抽取了部分学生的成绩，（得分取正整数，满分为100分）进行了统计，请你根据下面尚未完成并有局部污损的频率分布表和频率分布直方图，解答下列问题。

频率分布表
分组	频数	频率
50．5—60．5	4	0．08
60．5—70．5	8	0．16
70．5—80．5	10	0．20
80．5—90．5	16	0．32
90．5—100．5
合计

（1）填空频率分布表中的二个空格；　　

（2）补全频率分布直方图；

（3）在该问题中的样本容量是多少？答_______________；

（4）全体参赛学生中，竞赛成绩落在哪组内的人数最多？答_______________；

（5）若成绩在90分以上（不含90分）为优秀，则成绩优秀的约为多少人？答__________。

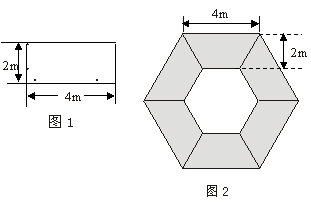
23．（本题7分）现有六块相同的矩形铁皮，如图（1），要焊成如图（2）所示的中空的正六边形广告牌（块与块无间隙不计算焊接面积）

（1）如何切割矩形铁皮，请在图（1）中画出虚线表示，并简要说明理由。

（2）计算这种广告牌的面积。

 

24．（本题8分）已知是关于的一元二次方程的两个实数根，（1）若满足，求m的值；（2）当m为何值时，方程两根的平方和最小。

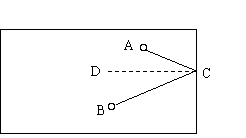
25．（本题8分）中国的“台球神童”丁俊辉2005年12月一举夺得英国斯诺克锦标赛冠军，为中国争得这个比赛项目的第一块金牌。你知道吗，台球在运动时有这样的规律，当球在运动过程中碰到台壁时，将以一定的角度反弹，如图所示∠ACD=∠BCD，现在在球台中有一个白球A要通过打右台壁反弹到红球B，A距离右台壁1.5米，B距离右台壁2米；A距离上台壁0.25米，B距离下台壁0.4米,标准台球桌宽为2.05米,问白球打到右台壁什么位置处，刚好能经过一次反弹击中红球？

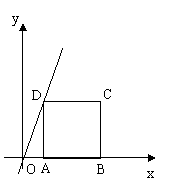
26．（本题8分）如图正方形ABCD的一边AB在x轴正半轴上，点C坐标是（3，2），将直线OD沿x轴正方向平移m个单位。

（1）如果直线OD在移动过程中与边CD有交点，试问m的取值范围，并用m的代数式表示交点坐标；

（2）若将OD在移动过程中扫过的正方形面积设为S，当S=时，求m的值。

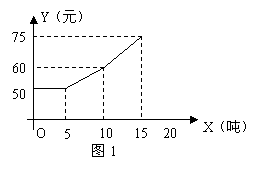
27．（本题12分）通宁公路收费站对货车收费标准为：载重量不超过5吨，收费为50元/辆，为限制过重货车通过，当载重量超过5吨时，超过部分按不同吨位段上浮，支付费用y（元）与载重量x（吨）的函数关系如图1所示。

（1）请写出支付费用y（元）与载重量x（吨）之间的函数解析式；

（2）某公司接受从南通运往泰州甲类货物52吨和乙类货物40吨的任务，计划租用A、B两种型号车10辆，其满载量（同时装载两种货物最多运输量/辆）如图2

满载　　货 　　量　 类 型号	甲（吨/辆）	乙（吨/辆）
A	6	3
B	4	8

（1）问公司经理如何安排车辆能完成任务，共有几种方案；

（2）请选择一种方案计算出过路费用。

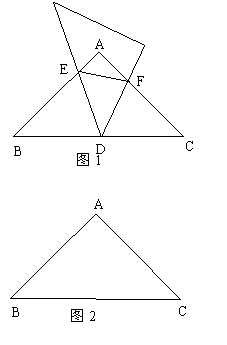
28．（本题12分）在△ABC中AB=AC=，∠A=90⁰，取一块45⁰的直角三角板并将45⁰角的顶点置于BC边的中点D处，其两边分别交AB、AC边于E、F，三角板绕点D旋转。

（1）三角板绕至图（1）位置时，写出图中共有几对相似三角形？并请选一组进行证明；

（2）设BE=x，CF=y，求y与x的函数关系式，并写出x的取值范围；

（3）若以D为圆心的圆与AB相切，①试探究直线EF与⊙D的位置关系，并证明你的结论；②如果E点在BA的延长线上，F点仍在AC上，试问①中探究的结论还成立吗？请简要说明理由。