初三数学第三次联考试题

初三数学第三次联考试题

卷首语：请同学们拿到试卷后，不必紧张，用半分钟整理一下思路，要相信我能行。

一、选择题（本题有12小题，每小题4分，共48分）

1、-2的倒数是（　　　）

A、　　　　B、2　　　　　　　C、　　　　　 D、-2

2、据统计全球每分钟约有吨污水排入江河湖海，这个排污量用科学记数法表示为_______吨。（　　　）

A、8.5×10⁵　　　　　　　　　　　　B、85×10⁵　　　　　

C、8.5×10⁶　　　　　　　　　　　　D、0. 85×10⁶

3、圆柱的高为6cm，它的底面半径为3cm，则这个圆柱的侧面积是（　　　）

A、18cm²　　　　 B、36cm² C、18cm²D、36cm²

4、如图水杯的俯视图是（　　　）

A　　　　　　　 　　B　　　　　　　　　 C　　　　　　　　　 D

5、直角边边长分别为3，4的直角三角形的外接圆半径是（　　　）

A、2　　　　　　　B、　　　　　C、　　　　　 D、1

6、如图的转盘被划分成六个相同大小的扇形，并分别标上1，2，3，4，5，6这六个数字，指针停在每个扇形的可能性相等，四位同学各自发表了下述见解：

甲：如果指针前三次都停在了3号扇形，下次就一定不会停在3号扇形了

乙：只要指针连续转六次，一定会有一次停在6号扇形

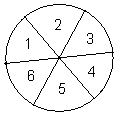丙：指针停在奇数号扇形的概率和停在偶数号扇形的概率相等

丁：运气好的时候，只要在转动前默默想好让指针停

在6号扇形，指针停在6号扇形的可能性就会加大。

你认为哪位同学的见解正确（　　　）

A、甲　　　　　　B、乙　　　　　　C、丙　　　　　　D、丁

7、在下面的四个车标中，是中心对称图形的是(　　)

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 

　　　A　　　　　　　　  B　　　　　　  C　　　　　　　　　 D

8、关于x的方程x²-7x-7k=0有实根，则k的取值范围（　　　）

A、k>　　　　　　　　　 B、k≥且k≠0　

C、k≥　　　　　　　　　 D、k>且k≠0

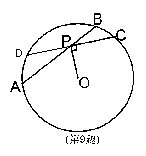
9、如图：弦AB与CD相交于点P，连OP，且OP ⊥CD，

若AP=4，PB=2则PC的长是（　　　）

A、　　　　 B、　　　　　　　C、2　　　　　　　D、3

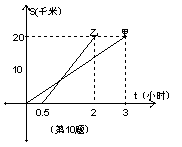10、甲，乙两同学从A地出发骑自行车在同一条路上行驶到距A地20千米的B地，他们离出发地的距离S（千米）和行驶时间t（小时）之间的函数关系的图形如图所示，根据图中提供的信息符合图象描述的说法是（　　 ）

A、甲在行驶过程中休息了一会

B、乙在行驶过程中没有追上甲

C、乙比甲先到达B地

D、甲行驶速度比乙的行驶速度快

11、某服装超市以每套648元的价格卖出两套不同品牌的

西服，其中一套盈利20%，另一套亏本20%,在这次买卖中，

这家商店（　　  ）

A、赔了54元　　　　　　　B、赚了54元　　　　　　　C、不赔不赚　　　　D、赚了50元

12、有一张矩形纸片ABCD，AB=2.5，AD=1.5将纸片折叠，使AD边落在AB边上折痕为AE，再将△AED以DE为折痕向右折叠，AE与BC交于点F，则CF的长为（　　 ）

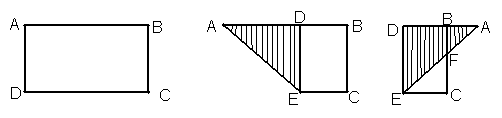
A、0.5　　　　　　　　　B、0.75　　　　　　　　C、1.25　　　　　　　　D、1

二、填空题（本题有6小题，每题5分，共30分）

13、化简3a－5a=_________

14、方程的解为_________

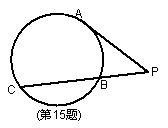
15、如图，PA切⊙O于A，PBC是割线，

已知AP=cm，BC=2cm，则PB=_______

16、汽车刹车距离S­_（m）与速度V_（km/h）之间的函数关系是S=，在一辆车速为100 Km/h汽车前方80m处发现一辆故障车，此时刹车_______有危险。（填会或不会）

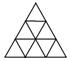
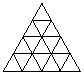
17、请根据下列△叠加的规律，探求小△叠加的层数与小△个数之间的关系，当叠加n层时小△个数有___________（用n的代数式表示）

　　　 ……  

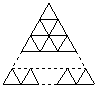
 1层　　 2层　　　　3层　　　　 4层　　　　　 　　　 n层

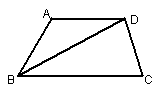18、在梯形ABCD中，AD∥BC，BC=BD，AD=AB=4cm，∠A=120º，

则梯形ABCD的面积等于_____________。

三、解答题（本题有7小题，共72分）

19、（本小题8分）化简

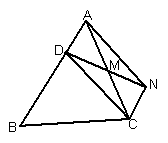20、（本小题8分）如图，已知D是△ABC的边AB上一点，CN∥AB，DN交AC于M，若MA=MC，求证：四边形ADCN为平行四边形。

21、（本小题8分）甲乙两人在相同条件下各射靶10次，每次射靶的成绩情况如图。

（1）请填写下表

	平均数	方差	命中9环及9环以上次数
甲		1.2	1
乙	7	5.4

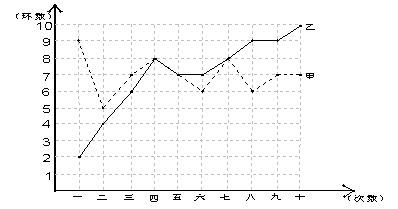（2）请从某一角度对这次测

试结果进行分析，并根据分

析结果选择指派哪位选手参

加比赛。

22、（本小题10分）如图，路灯沿灯罩边缘射出的光线与地面水平线的交点为A，∠A=50 º，A与灯柱底部B的距离为6米，灯柱上方的杠杆ED长1米，EF⊥AB于F，若EF所在直线是灯罩的对称轴，求灯柱上被灯光直接照射的BC的长（精确到0.01米）

(sin50°=0.7660 cos50°=0.6428　tan50°=1.1918 cot50°=0.8391）

23、（本小题12分）如图，在Rt△ABC中∠ACB=90°，BC=4 cm，AC=b cm，且BC、AC是方程的两根，

（1）求m和b的值

（2）若△A´B´C´与△ABC完全重合，当△ABC原定不动，将△A´B´C´沿BC所在直线向右以1厘米/秒的速度移动，设移动x秒后， △A´B´C´与△ABC的重叠部分的面积为y cm²，求y与x之间的函数关系式。

	M

24、（本小题12分）请先阅读下面材料

式子“1+2+3+……+100”表示从1开始到100的连续自然数的和，由于式子较长，书写起来不方便，为了简便起见，我们把“1+2+3+……+100”表示成，这里的“∑”是求和符号，再如“1+3+7+……+2005”（即从1开始到2006的所有奇数和）可以表示成，又如“1³+2³+3³+4³+……+20³”可以表示成，又如b₁+b₂+b₃+……b₁₀₀可以表示成，根据以上材料，回答下列问题。

（1）2+4+6+……+2006（即从2开始到2006的连续偶数的和）用求和符号可以表示成_____________

（2）计算=________　  （填写计算结果）

（3）若有60个数x₁，x₂，x₃，……x₆₀平均数为a

 用求和符号表示a=___________

25、（本小题14分）如图，P为x轴正半轴上一点，半圆P交x轴于A、B两点，交y轴于C点，弦AE分别交OC、CB于D、F，已知弧AC=弧CE。

（1）求证：AD=CD；

（2）若DF=，tan∠ECB=，点C关于x轴的对称点为C´，求经过A、B、C´三点的抛物线的解析式。

P

（3）在（2）条件下，设M为x轴上一点，OM=AE，是否存在过点M直线，使该直线与（2）中所得的抛物线的两个交点到y轴距离相等？若存在，求出这条直线的解析式；若不存在，请说明理由。