初三数学第三次月考
一、选择题:（每题3分，共30分）
1、如果
有意义，则
的取值范围是（ ）
（A）
（B）
（C）
（D）
2、二次函数
的图象向右平移3个单位，得到新的图象的函数表达式是
(A)
(B)
(C)
(D)
3. 如图，A、B、C、是⊙O上的三点，∠BAC=45°，
则∠BOC的大小是
A．90° B．60° C．45° D．22.5°
4、下列二次根式中，最简二次根式是（ ）
（A）
（B）
（C）
（D）
| |
－9＝0的根是(
)
(A)x＝3
(B)x＝
(C) 
(D) 
＝ 
＝－
6．关于x的方程
有两个不相等的实数根，则k的取值范围是 （ ）
A．k＜-1 B．k≥-4 C．k＜1 D．k≥4
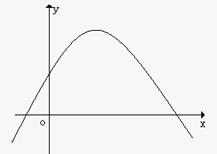
7．二次函数y=ax2+bx+c的图象图所示，则下列结论：
①a＞0，②c＞0，③b2-4ac＞0，其中正确的个数是( )
A、0个 B、1个 C、2个 D、3个
8．点P(2,3)关于x轴的对称点为Q（m,n ）,点Q关于Y轴的对称点为M(x,y)，由点M
关于原点的对称点是
A．(－2,3) B．(2,－3) C．(－2,－3) D．（2，3）
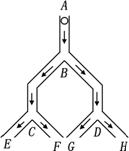9．如图 ，一个小球从A点沿制定的轨道下落，在每个交叉口都有向左或向右两种机会均等的结果，小球最终到达H点的概率是
A．1/2 B．1/4 C．1/6 D．1/8
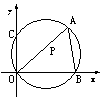10、如图，在平面直角坐标系中，已知⊙P经过原点O，与x轴、y轴分别交于B、C两点，OA与⊙P相交于点A，∠OAB＝60°，则下列结论正确的是（ ）
（A）OB＝2OC
（B）OB＞2OC
（C）
（D）
二、填空，（每题4分 ，共28分）
1、计算：
＝ .
2．抛物线 
的顶点坐标为
3、写出一个根为2,且二次项系数为1的一元二次方程 （只需写出一个方程即可）.
4、化简：
=
5．对于任意实数m、n都有m▼n=m+2n，m▲n：2m-n，
则[2▼（一1)]▲(一2)=_____________
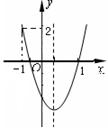6. 如图，二次函数
的图象开口向上,图像经过点（-1，2）和（1，0）且与y轴交于负半轴．
第（1）问：给出四个结论：①＞0；②
＞0；③
＞0； ④a+b+c=0
其中正确的结论的序号是 ▲ （答对得4分，少选、错选
均不得分）．
第（２）问：给出四个结论：①abc＜0；②2a+＞0；③a+c=1；
④a＞1．其中正确的结论的序号是 ▲ （答对得4分，少选、错选均不得分）．
三、解答题
1 、（20分）
（1）、解方程 x2－2x－2 = 0 （2）、计算：
2、
（12分）如图7，⊙O的直径AB=6cm，D为⊙O上一点，∠BAD=30°，过点D的切线交AB的延长线于点C。
求：(1)∠ADC的度数；
(2)AC的长。
3、 （本题满分10分）某种服装，平均每天可销售20件，每件盈利44元.若每件降价1元,则每天可多销售5件.如果每天要盈利1600元，请你帮忙算算，每件应降价多少元？
解:
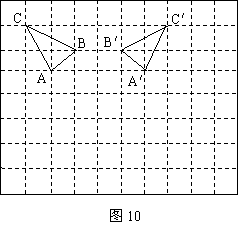
4、（12分）19．如图10，是一个8×10正方形格纸，△ABC中A点坐标为（－2，1）。
（1）△ABC和△A＇B＇C＇满足什么几何变换（直接写答案）？
（2）作△A＇B＇C＇关于x轴对称图形△A＇＇B＇＇C＇＇；
（3）△ABC和△A＇＇B＇＇C＇＇满足什么几何变换？求A＇＇、B＇＇、C＇＇三点坐标（直接写答案）。
 |
5、（本题满分12分）阅读理解：
材料1：设一元二次方程
有两个实根
由求根公式
得到
它描述了一元二次方程的根与系数间的一种必然关系.
材料2：已知关于x的方程：
的两个实数根的平方之和等于56，求m 的值.
小明同学的解答过程如下：
解：设这个方程两个实数根为，由材料1可知：
， 
，
∴ 
由条件有
，即有
∴
解得：
∴当
时，方程的两个实数根的
平方和等于56.
问题：小明同学的解答正确吗？若不正确请指出错误的原因，并写出正确的答案.
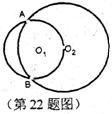
6、（13分）己知：如图，
和
相交于A、B两点，经过点
，点C在
上运动
(点C不与A、B重合)，AC的延长线交于P，连结AB、BC、BP；
(1)按题意将图形补充完整；
（2)当点C在上运动时，图中不变的角有________________________
(将符合要求的角都写上)
(3)线段BC、PC的长度存在何种关系?写出结论，并加以证明：
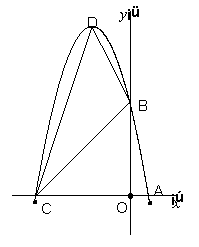
7．（13分）、.已知：
是方程
的两个实数根，且
，抛物线
的图像经过点A(
)、B(
).
(1) 这个抛物线的解析式是_______________________________
(2)
设（1）中抛物线与
轴的另一交点为C,抛物线的顶点为D，试求出点C、D的坐标和△BCD的面积；（注：抛物线
的顶点坐标为（
），）
(3)
P是线段OC上的一点，过点P作PH⊥轴，与抛物线交于H点，若直线BC把△PCH分成面积之比为2：3的两部分，请求出P点的坐标.