初中毕业学业与升学考试数学试卷3新课程)
本试卷满分为150分,考试时间为120分钟.
一、选择题(每小题只有一个正确选项,将正确选项的序号填入题后的括号内.10小题,每小题3分,共30分)
1.![]() 的值是( )
的值是( )
A.1 B.2 C.![]() D.
D.![]()
2.下列运算中,不正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.方程![]() 的解是( )
的解是( )
A.1 B.2 C.3 D.![]()
4.下列物体中,是同一物体的为( )
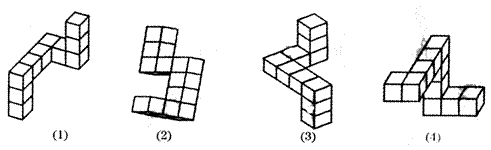
A.(1)与(2) B.(1)与(3)
C.(1)与(4) D(2)与(3)
 5.“数轴上的点并不都表示有理数,如图中数轴上的点
5.“数轴上的点并不都表示有理数,如图中数轴上的点![]() 所表示的数是
所表示的数是![]() ”,这种利用图形直观说明问题的方式体现的数学思想方法叫( )
”,这种利用图形直观说明问题的方式体现的数学思想方法叫( )
A.代入法
B.换元法
C.数形结合的思想方法
D.分类讨论的思想方法
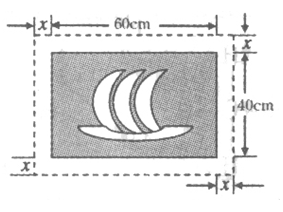
6.在一幅长60cm,宽40cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图所示.如果要使整个挂图的面积是![]() ,设金色纸边的宽为
,设金色纸边的宽为![]() ,那么
,那么![]() 满足的方程是( )
满足的方程是( )
A.![]()
B.![]()
C.![]()
D.![]()
 7.夏天,一杯开水放在桌子上,杯中水的温度
7.夏天,一杯开水放在桌子上,杯中水的温度![]() 随时间
随时间![]() 变化的关系的大致图象是( )
变化的关系的大致图象是( )
 8.如图,
8.如图,![]() 的边长都大于2,分别以它的顶点为圆心,1为半径画弧(弧的端点分别在三角形的相邻两边上),则这三条弧的长的和是( )
的边长都大于2,分别以它的顶点为圆心,1为半径画弧(弧的端点分别在三角形的相邻两边上),则这三条弧的长的和是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 9.一人乘雪橇沿如图所示的斜坡笔直滑下,滑下的距离
9.一人乘雪橇沿如图所示的斜坡笔直滑下,滑下的距离![]() (米)与时间
(米)与时间![]() (秒)间的关系式为
(秒)间的关系式为![]() ,若滑到坡底的时间为2秒,则此人下滑的高度为( )
,若滑到坡底的时间为2秒,则此人下滑的高度为( )
A.24米 B.12米
C.![]() 米 D.6米
米 D.6米
10.某超市(商场)失窃,大量的商品在夜间被罪犯用汽车运走.三个嫌疑犯被警察局传讯,警察局已经掌握了以下事实:(1)罪犯不在甲、乙、丙三人之外;(2)丙作案时总得有甲作从犯;(3)乙不会开车.在此案中,能肯定的作案对象是( )
A.嫌疑犯乙 B.嫌疑犯丙 C.嫌疑犯甲 D.嫌疑犯甲和丙
二、填空题(把答案填在题中的横线上.8小题,每小题4分,共32分)
11.某种感冒病毒的直径是0.米,用科学记数法表示为 米.
 12.如图中两圆的位置关系是 (相交,外切,外离).
12.如图中两圆的位置关系是 (相交,外切,外离).
13.反比例函数![]() 的图象位于 象限.
的图象位于 象限.
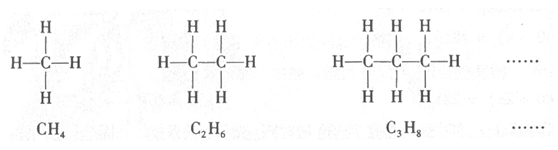
14.下列是三种化合物的结构式及分子式,则按其规律第4个化合物的分子式为 .
15.小明将一把钥匙放进自己家中的抽屉中,他记不清到底放进三个抽屉中的哪一个了,那么他一次选对抽屉的概率是 .
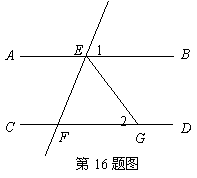
16.如图,![]() ,
,![]() 平分
平分![]() ,若
,若![]() ,则
,则![]() .
.
 17.
17.![]() 为等边三角形,
为等边三角形,![]() 分别在边
分别在边![]() 上,且
上,且![]() ,则
,则![]() 为 三角形.
为 三角形.
18.二次函数![]() 图象上部分点的对应值如下表:
图象上部分点的对应值如下表:
|
|
|
|
| 0 | 1 | 2 | 3 | 4 |
|
| 6 | 0 |
|
|
|
| 0 | 6 |
则使![]() 的
的![]() 的取值范围为 .
的取值范围为 .
三、解答题(解答时,必须写出必要的解题步骤.5小题,共38分)
19.(6分)先化简,再求值:![]() ,其中
,其中![]() .
.
20.(8分)有7名同学测得某楼房的高度如下(单位:米):
29,28.5,30,30,32,31,33.
(1)求这组数据的中位数、众数、平均数;
(2)你认为此楼房大概有多高?

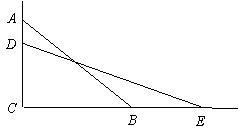
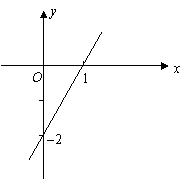 21.(8分)一次函数图象如图所示,求其解析式.
21.(8分)一次函数图象如图所示,求其解析式.
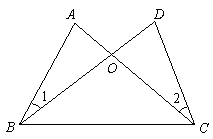
22.(8分)如图,已知![]() .求证:
.求证:![]() .
.
23.(8分)为节约用电,某学校在本学期初制定了详细的用电计划.如果实际每天比计划多用2度电,那么本学期的用电量将会超过2990度;如果实际每天比计划节约2度电,那么本学期的用电量将不超过2600度.若本学期的在校时间按130天计算,那么学校原计划每天用电量应控制在什么范围内?
四、解答题(解答时,必须写出必要的解题步骤.5小题,共50分)
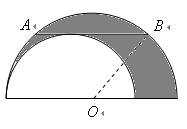
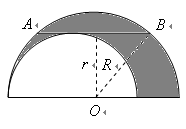
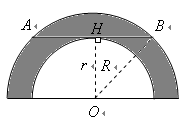
24.(8分)如图是两个半圆,点![]() 为大半圆的圆心,
为大半圆的圆心,![]() 是大半圆的弦关与小半圆相切,且
是大半圆的弦关与小半圆相切,且![]() .问:能求出阴影部分的面积吗?若能,求出此面积;若不能,试说明理由.
.问:能求出阴影部分的面积吗?若能,求出此面积;若不能,试说明理由.
 25.(10分)一架长5米的梯子
25.(10分)一架长5米的梯子![]() ,斜立在一竖直的墙上,这时梯子底端距墙底3米.如果梯子的顶端沿墙下滑1米,梯子的底端在水平方向沿一条直线也将滑动1米吗?用所学知识,论证你的结论.
,斜立在一竖直的墙上,这时梯子底端距墙底3米.如果梯子的顶端沿墙下滑1米,梯子的底端在水平方向沿一条直线也将滑动1米吗?用所学知识,论证你的结论.
26.(10分)如图,![]() 为正方形
为正方形![]() 边
边![]() 的中点,
的中点,![]() 是
是![]() 延长线上的一点,
延长线上的一点,![]() ,且交
,且交![]() 的平分线于
的平分线于![]() .
.
(1)求证:![]() ;
;
(2)若将上述条件中的“![]() 为
为![]() 边的中点”改为“
边的中点”改为“![]() 为
为![]() 边上任意一点”,其余条件不变,则结论“
边上任意一点”,其余条件不变,则结论“![]() ”成立吗?如果成立,请证明;如果不成立,说明理由.
”成立吗?如果成立,请证明;如果不成立,说明理由.

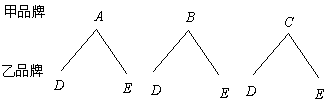
27.(10分)某公司现有甲、乙两种品牌的计算器,甲品牌计算器有![]() 三种不同的型号,乙品牌计算器有
三种不同的型号,乙品牌计算器有![]() 两种不同的型号,新华中学要从甲、乙两种品牌的计算器中各选购一种型号的计算器.
两种不同的型号,新华中学要从甲、乙两种品牌的计算器中各选购一种型号的计算器.
(1)写出所有的选购方案(利用树状图或列表方法表示);
(2)如果(1)中各种选购方案被选中的可能性相同,那么![]() 型号计算器被选中的概率是多少?
型号计算器被选中的概率是多少?
(3)现知新华中学购买甲、乙两种品牌计算器共40个(价格如图所示),恰好用了1000元人民币,其中甲品牌计算器为![]() 型号计算器,求购买的
型号计算器,求购买的![]() 型号计算器有多少个?
型号计算器有多少个?

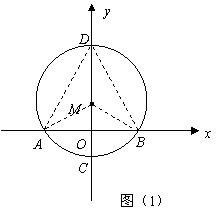
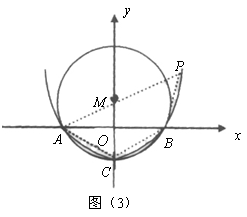
28.(12分)如图,在![]() 中,
中,![]() 所对的圆心角为
所对的圆心角为![]() ,已知圆的半径为2cm,并建立如图所示的直角坐标系.
,已知圆的半径为2cm,并建立如图所示的直角坐标系.
(1)求圆心![]() 的坐标;
的坐标;
(2)求经过![]() 三点的抛物线的解析式;
三点的抛物线的解析式;
(3)点![]() 是弦
是弦![]() 所对的优弧上一动点,求四边形
所对的优弧上一动点,求四边形![]() 的最大面积;
的最大面积;
(4)在(2)中的抛物线上是否存在一点![]() ,使
,使![]() 和
和![]() 相似?若存在,求出点
相似?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

初中毕业学业与升学考试(新课程)
数学试题参考答案与评分标准
一、选择题:每小题3分,共30分
ACDBC ABDBC
二、填空题:每小题4分,共32分
11.![]() 12.外离 13.一,三 14.
12.外离 13.一,三 14.![]()
15.![]() 16.
16.![]() 17.正 18.
17.正 18.![]()
三、解答题:共38分
19.本小题满分6分
解:原式![]() ,······································································································· 4分
,······································································································· 4分
当![]() 时,原式
时,原式![]() .······················································································ 6分
.······················································································ 6分
说明:会运用分配律且对者给2分,会用公式![]() 且对者给1分,若先通分且对者给2分.
且对者给1分,若先通分且对者给2分.
20.本小题满分8分
解:(1)在这组数据中,中位数是30,········································································· 2分
众数是30,··················································································································· 4分
平均数是30.5;············································································································· 6分
(2)该楼房大概高30米(未写单位不扣分)······························································· 8分
21.本小题满分8分
解:设一次函数解析式为![]() ,············································································ 1分
,············································································ 1分
则![]() ··········································································································· 5分
··········································································································· 5分
解得![]()
所以,一次函数解析式为![]() .············································································ 8分
.············································································ 8分
说明:只要求出![]() 无最后一步不扣分.
无最后一步不扣分.
22.本小题满分8分
说明: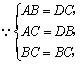 ······································································································· 2分
······································································································· 2分
![]() .····································································································· 4分
.····································································································· 4分
![]() .················································································································ 6分
.················································································································ 6分
又![]() ,
,
![]() .·················································································································· 8分
.·················································································································· 8分
23.本小题满分8分
解:设学校原计划每天用电量为![]() 度,·········································································· 1分
度,·········································································· 1分
依题意得![]() ························································································· 5分
························································································· 5分
解得![]() .
.
即学校每天的用电量,应控制在21~22度(不包括21度)范围内.····························· 8分
说明:只要求出![]() ,无最后一步不扣分.
,无最后一步不扣分.
四、解答题:共50分
24.本小题满分8分
解法1:
能(或能求出阴影部分的面积).·················································································· 1分
设大圆与小圆的半径分别为![]() ,················································································ 2分
,················································································ 2分
作辅助线如图所示(作对),························································································· 4分
可得![]() ,······································································································· 6分
,······································································································· 6分
![]() .··················································································· 8分
.··················································································· 8分
解法2:
能(或能求出阴影部分的面积).·················································································· 1分
设大圆与小圆的半径分别为![]() ··················································································· 2分
··················································································· 2分
平移小半圆使它的圆心与大半圆的圆心![]() 重合(如图).··············································· 3分
重合(如图).··············································· 3分
作![]() 于
于![]() ,则
,则![]() ,
,![]() .··························································· 5分
.··························································· 5分
![]() ,············································································································ 6分
,············································································································ 6分
![]() .······································································· 8分
.······································································· 8分
25.本小题满分10分
是.······························································································································ 2分
证明1:
在![]() 中,
中,![]() 米.·········································· 4分
米.·········································· 4分
![]() 米.········································································································· 6分
米.········································································································· 6分
在![]() 中,
中,![]() 米.········································ 8分
米.········································ 8分
![]() .即梯子底端也滑动了1米.···························································· 10分
.即梯子底端也滑动了1米.···························································· 10分
证明2:
在![]() 中,
中,![]() 米.·········································· 4分
米.·········································· 4分
![]() 米.········································································································· 6分
米.········································································································· 6分
可证![]() .························································································· 8分
.························································································· 8分
![]() 米.
米.
![]() .即梯子底端也滑动了1米.···························································· 10分
.即梯子底端也滑动了1米.···························································· 10分
26.本小题满分10分
证明:(1)取![]() 的中点
的中点![]() ,连结
,连结![]() .······································································ 1分
.······································································ 1分
易证![]() ,
,
![]() ······································································································· 3分
······································································································· 3分
![]() .·············································································································· 4分
.·············································································································· 4分

(2)结论“![]() ”仍成立.················································································ 5分
”仍成立.················································································ 5分
证明如下:
在![]() 上截取
上截取![]() ,连结
,连结![]() .··········································································· 6分
.··········································································· 6分
![]() ,
,
![]() .··············································································································· 7分
.··············································································································· 7分

![]() ,
,
![]() .···································································································· 8分
.···································································································· 8分
又![]() ,
,
![]() .··································································································· 9分
.··································································································· 9分
![]() .············································································································· 10分
.············································································································· 10分
 27.本小题满分10分
27.本小题满分10分
解:(1)树状图表示如下:
····································································································································· 2分
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
列表表示如下:
····································································································································· 2分
有6种可能结果:![]() .··································· 3分
.··································· 3分
说明:用其它方式表达选购方案且正确者,只给1分.
(2)因为选中![]() 型号计算器有2种方案,即
型号计算器有2种方案,即![]() ,所以
,所以![]() 型号计算器被选中的概率是
型号计算器被选中的概率是![]() . 5分
. 5分
(3)由(2)可知,当选用方案![]() 时,设购买
时,设购买![]() 型号,
型号,![]() 型号计算器分别为
型号计算器分别为![]() 个,
个,
根据题意,得![]() 解得
解得![]()
经检验不符合题意,舍去;··························································································· 7分
当选用方案![]() 时,设购买
时,设购买![]() 型号、
型号、![]() 型号计算器分别为
型号计算器分别为![]() 个,
个,
根据题意,得![]() 解得
解得![]() ································································ 9分
································································ 9分
所以新华中学购买了5个![]() 型号计算器.···································································· 10分
型号计算器.···································································· 10分
说明:设购买![]() 型号计算器
型号计算器![]() 台,
台,![]() (或
(或![]() )型号计算器为
)型号计算器为![]() 个,用一元一次方程解答,同样给分.
个,用一元一次方程解答,同样给分.
28.本小题满分12分
解:(1)如图(1),连结![]() .
.
 则
则![]() ,
,
![]() ,
,![]() .···················································································· 2分
.···················································································· 2分
![]() ,
,![]() .······················································································ 3分
.······················································································ 3分
(2)由![]() 三点的特殊性与对称性,
三点的特殊性与对称性,
知经过![]() 三点的抛物线的解析式为
三点的抛物线的解析式为![]() .·················································· 4分
.·················································· 4分
![]() ,
,![]() ,
,
![]() .···································································································· 5分
.···································································································· 5分
![]() .
.
![]() .·············································································································· 6分
.·············································································································· 6分
说明:只要求出![]() ,无最后一步不扣分.
,无最后一步不扣分.
(3)![]() ,又
,又![]() 与
与![]() 均为定值,··································· 7分
均为定值,··································· 7分
![]() 当
当![]() 边
边![]() 上的高最大时,
上的高最大时,![]() 最大,此时点
最大,此时点![]() 为
为![]() 与
与![]() 轴的交点,如图(1).
轴的交点,如图(1).
····································································································································· 8分
![]() .········· 9分
.········· 9分
(4)方法1:
如图(2),![]() 为等腰三角形,
为等腰三角形,![]() ,
,

![]() 等价于
等价于![]() .······················ 10分
.······················ 10分
设![]() 且
且![]() ,则
,则![]() ,
,
![]() .······································································································ 11分
.······································································································ 11分
又![]() 的坐标满足
的坐标满足![]() ,
,
![]() 在抛物线
在抛物线![]() 上,存在点
上,存在点![]() ,
,
使![]() .
.
由抛物线的对称性,知点![]() 也符合题意.
也符合题意.
![]() 存在点
存在点![]() ,它的坐标为
,它的坐标为![]() 或
或![]() .···························································· 12分
.···························································· 12分
说明:只要求出![]() ,
,![]() ,无最后一步不扣分.下面的方法相同.
,无最后一步不扣分.下面的方法相同.
方法2:
如图(3),当![]() 时,
时,![]() ,又由(1)知
,又由(1)知![]() ,
,
![]() 点
点![]() 在直线
在直线![]() 上.
上.
设直线![]() 的解析式为
的解析式为![]() ,
,
将![]() 代入,解得
代入,解得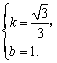
![]() 直线
直线![]() 的解析式为
的解析式为![]() .··········································································· 10分
.··········································································· 10分
解方程组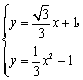 得
得![]() .············································································ 11分
.············································································ 11分
又![]() ,
,![]() .
.
![]() ,
,![]() .
.
![]() 在抛物线
在抛物线![]() 上,存在点
上,存在点![]() ,使
,使![]() .
.
由抛物线的对称性,知点![]() 也符合题意.
也符合题意.
![]() 存在点
存在点![]() ,它的坐标为
,它的坐标为![]() 或
或![]() .···························································· 12分
.···························································· 12分
方法3:
如图(3),![]() 为等腰三角形,且
为等腰三角形,且![]() ,设
,设![]() ,则
,则
![]() 等价于
等价于![]() ,
,![]() .·········································· 10分
.·········································· 10分
当![]() 时,得
时,得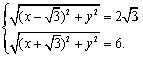
解得![]() .··········································································································· 11分
.··········································································································· 11分
又![]()
![]() 的坐标满足
的坐标满足![]() ,
,
![]() 在抛物线
在抛物线![]() 上,存在点
上,存在点![]() ,使
,使![]() .
.
由抛物线的对称性,知点![]() 也符合题意.
也符合题意.
![]() 存在点
存在点![]() ,它的坐标为
,它的坐标为![]() 或
或![]() .
.