初中毕业会考数学摸拟测试二
总分 120分 时量 90分钟
一、填空题（共10小题，每题5分，合计50分）
1．如果方程x2+(k2-4)x+k+1=0的两实根互为相反数，那么k=______。
2．已知半径为1cm和2cm的两个圆外切于点P，则点P到外公切线的距离为______。
3．今有浓度分别为3%、8%、11%的甲、乙、丙三种盐水50千克、70千克、60千克,现要用甲、乙、丙这三种盐水配制浓度为7%的盐水100千克,则丙种盐水最多可用
千克.
4．已知方程m2x2-(4m+3)x+4=0有两个不相等的实数根x1、x2，设S=
，则S的取值范围是______。
5．在△ABC中，O是外心，I是内心，若∠BOC=100°，则∠BIC的度数是______。
6．已知二次函数已知二次函数y = 2x 2 –px + 5，当x³ -2时，y随x的增加而增加，那么当x = p时，对应的y的值的取值范围为 。
7．已知⊙O为正△ABC的外接圆，OD∥AB(其中D为外接圆上的点)，则∠BCD=______度。
8．有张圆桌放在房间角落，与两面互相垂直的墙壁都接触，飞来一只蝉，停在圆桌边上的的A处，没提防圆桌中心的O处有一只螳螂，如果A点离两墙壁的距离分别是8cm和9cm，则螳螂捕蝉归少需走
cm的路程。（精确到整数）
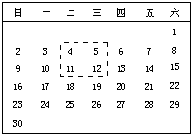
9．如图，这是2006年6月份的日历．现用一个矩形在表中任意框出4个数
，请用一个等式表示
、
、
、
之间的关系：
．
10．观察下列方程：⑴
；⑵
；
⑶
；……按此规律写出关于
的第
个
方程为 ，此方程的解为 ．
二、选择题（共5小题，每题4分，合计20分）
11．已知点P的坐标为(x, y)且
，则点P关于原点的对称点P，的坐标是( )
A、(-1，
) B、(-1，
) C、(1，) D、(1，)
12．设
，
，
，则a，b，c之间的大小关系是( )
A、c＞b＞a B、a＞c＞b C、b＞a＞c D、a＞b＞c
13．制作一个圆锥模型，其侧面是用一个半径为9cm，圆心角为240°的扇形铁皮围成的，则圆锥底面半径为( )
A、4cm B、3cm C、6cm D、12cm
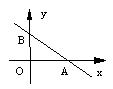
14.右图是一次函数
的图象，那么△AOB的面积等于( )
A、
B、
C、
D、
15．已知△ABC的三边长分别为a、b、c，面积为S；△DEF的三边长分别为d、e、f，面积为M，且a＞d,b＞e,c＞f，则S和M的关系为（ ）。
A、S＞M B、S＜M C、S = M D、不确定
三、解答题（共6小题，其中第16、17题6分，第18题8分，第19、20、21每题10分）
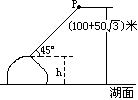16．如图，在山顶A处望见一艘飞艇停留在湖面上空(100+50
)米处，观察到飞艇底部标志P处的仰角为45°，又观其湖中之像的俯角为60°，试求山高h(观察时湖面处于平静状态)。
17．某水库建有10个泄洪闸，现在水库的水位已超过了安全线。上游河水还在按一不变的速度增加，为了防洪，需调节泄洪速度。假设每个闸门泄洪的速度相同，经测算，若打开一个泄洪闸，30个小时可降至安全线以下，现防洪指挥部要求在3个小时内使水位降至安全线以下，问至少同时打开几介闸门？
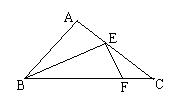
18．如图，在等腰直角△ABC中，AB = 1，∠A = 90°， 点E为腰AC的中点，点F在底边BC上，且FE⊥BE， 求△CEF的面积。
19．已知抛物线y = x 2 －2x＋m与x轴有两个不同交点A(x 1 , 0)、B(x 2 , 0)并且
x 1＜x 2，x 12＋x 22 = 4，①求这条抛物线；②设抛物线的顶点为C，P是抛物线上一点，且∠PAC = 90°，求P点坐标及△PAC内切圆的面积。
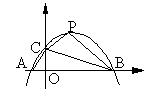
20．如图，抛物线y = －x 2 ＋ax＋b与x轴交于A、B两点，交y轴于点C，且∠BAC =a，∠ABC =b，tana－tanb= 2，∠ACB = 90°。①求抛物线的解析式；②若抛物线顶点为P，求S 四边形ABPC。
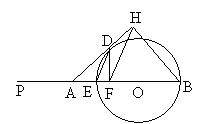
21．已知，如图，EB是⊙O的直径，且EB = 6，在BE的延长线上取点P，使EP = EB，A是EP上一点，过A作⊙O的切线，切点为D，过D作DF⊥AB于F，过B作AD的垂线BH，交AD的延长线于H。当点A在EP上运动，不与E重合时：⑴ 是否总有
，试证明你的结论；⑵设ED = x，BH = y，求y和x的函数关系，并写出x的取值范围。
