初中毕业会考数学摸拟测试一
（总分 120分 时间 90分钟）
一、填空题(共10小题，每题5分，合计50分)
1．已知函数
是反比例函数，则k=
。
2．一次函数y= ax+4(a为常数)，当x增加2时，y的值减少了3，则a= 。
3．已知m、n满足
，则
的值等于 。
4．如果x的不等式组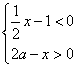
的解集是x<2，那么a的取值范围是
。
5．△ABC中，AB=5，中线AD=7，则AC边的取值范围是 。
6．△ABC中，AB=AC，高AD、BE相交于点H，AH=8，DH=1，则tanC的值是 。
7．如果菱形有一个角是45°，且边长是2，那么这个菱形两条对角线的乘积等于 。
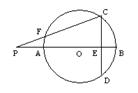8．如图，AB是圆O的直径，弦CD^AB于E，P是BA延长线上一点，连结PC交圆O于F，若PF=7，FC=13，PA:AE:EB=2:4:1，则CD长为
。
9．AB是圆O的直径，以AB为底的圆O的内接梯形对角线交点的轨迹
是 。
10．已知圆O的直径AB=2cm，过A点的两弦AC=
cm，AD=
cm，则ÐCAD所夹圆内部分的面积是 cm2。
二、选择题：(共5小题，每小题4分，共20分)
11．若0<a<1，则化简
的结果是
( )
A、-2a B、2a C、
D、
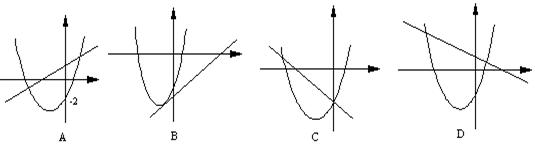
12．抛物线
与直线
的大致图象只可能是 ( )
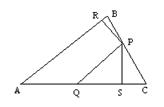13． 如图在△ABC中，P、Q分别是BC、AC上的点，作PR^AB，PS^AC，垂足分别是R、S，若AQ=PQ，PR=PS，下面三个结论① AS=AR ②PQ∥AB ③ △BRP≌△CSP，其中正确的是 ( )
A、① ② B、② ③ C、① ③ D、① ② ③
14．下列命题：① 若a>b>0，则以
为三边的三角形是直角三角形；②
用长为4、5、7、8的四条线段作边，其中以5、8作底可以作梯形；③ 等边三角形是轴对称图形，但不是中心对称图形；④
有两边和第三边上的高对应相等的两个三角形全等。其中假命题的个数是
( )
A、1个 B、2个 C、3个 D、4个
15．商场的自动扶梯在匀速上升，一男孩与一女孩在这自动扶梯上往上爬，已知男孩往上爬的速度是女孩往上爬的速度的2倍，男孩爬了27级到楼上，女孩爬18级到楼上，则从楼下到楼上自动扶梯的级数是 ( )
A、108 B、54 C、45 D、36
三、计算与证明：（每小题6分，共12分）
16．已知
，求
的值。（6分）
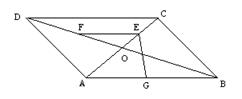
17．如图在平行四边形ABCD中，对角线AC、BD相交于O，BD=2AD，E、F、G分别为OC、OD、AB的中点，求证：(1) BE⊥AC (2) EG=EF （6分）
四、解答与证明（第18题8分，第19，20，21题各10分，共38分）
18．现有24个劳力和1000亩鱼塘可供对虾、大黄鱼、蛏子养殖，所需劳力与每十亩产值如下表所示。另外设对虾10x亩，大黄鱼10y亩，蛏子10z亩。
|
| 每十亩劳力 | 每十亩预计产值（万元） |
| 对 虾 | 0．3 | 2 |
| 大黄鱼 | 0．2 | 8 |
| 蛏子 | 0．1 | 1．6 |
⑴ 用x的式子分别表示y、z。⑵ 问如何安排劳力与养殖亩数收益最大？（8分）
19．已知关于x的方程
的两根的平方和是1，其中∠A为锐角三角形ABC的一个内角。① 求sinA的值。 ②
若△ABC的两边长x、y满足方程组
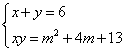(m为实数)，求△ABC的第三边。（10分）
20．已知抛物线
与x轴交于A、B两点，与y轴交于C点。(1) 求m的取值范围；(2) 若m≤0，直线y=kx-1，经过点A，与y轴交于点D，且AD×BD=2
，求抛物线的解析式。(3) 若点A在点B的左边，在第一象限内，(2)中所得抛物线上是否存在一点P，使直线PA平分△ACD的面积？若存在，求出P点坐标，若不存在，请说明理由。（10分）
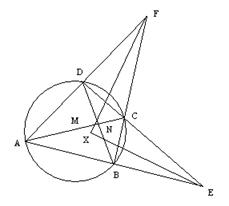
21．已知ABCD四点共圆，AB与DC相交于点E，AD与BC交于F，∠E的平分线EX与∠F的平分线FX交于X，M、N分别是AC与BD的中点，求证：(1) FX⊥EX，
(2) FX、EX分别平分∠MFN与∠MEN。（10分）
