初中毕业会考数学模拟测试（二）
一、选择题（每小题3分，共30分）
[ ]1.
的值等于毛
A．-3 B．3 C．±3 D．±9
[ ]2. 2003年10月15日9时10分,我国“神州”五号载人飞船准确进入预定轨道,16日5时59分,返回舱与推进艇分离,返回地面.其间飞船绕地球共飞行了14圈,飞行距离约为千米,用科学计数法表示为
A.5.91×107千米 B.5.91×108千 C.5.91×109千米 D.5.91×1010千米
[ ]3. 等腰三角形中,若一底角是41°,则它的顶角为
A . 41° B. 96° C. 139° D . 98°
[ ]4. 函数
的自变量x的取值范围是
A．x＜2 B．x≤2 C． x＞2 D．x＜2且x≠0
[ ]5.如果两个圆的半径分别为2cm和3cm,圆心距为4cm,,那么这两个圆的公切线有
A . 4条 B. 3条 C. 2条 D. 1条
[ ]6.下面的图形中,既是轴对称图形,又是中心对称图形的是
A. Q B. ¹ C. µ D. Y
[ ]7.中央电视台“开心辞典”栏目曾有这么一道题:圆的半径增加了两倍,那么圆的面积增加了
A . 4倍 B. 6倍 C. 8倍 D. 9倍
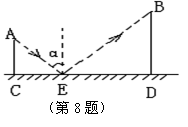[ ]8.如图,光线从A点出发经平面镜反射恰好照射到B点,若AC=2,
BD=4,CD=8,入射角为α,则tanα的值为
A . 
B. 
C. 
D. 2
[ ]9. (针孔成像问题)根据图中尺寸(AB∥A/B/),
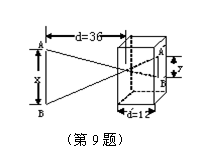那么物像长y (A/B/
的长) 与物长
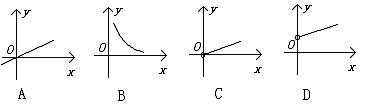
x (AB的长)之间函数关系的图象
大致是
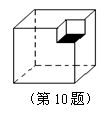[ ]10. 如图,从边长为10的正方体的一顶点处挖去一个边长为1 的小正方体,则剩下图形的表面积为( )
A. 600 B. 599 C. 598 D. 597
二、填空题 (本题共7小题,每小题4分,共28分.)
13.若二次三项式
能够分解为两个一次因式的乘积,且
为整数,则的值为(写出满足条件的一个值即可)________.
14.反比例函数
的图象在第二象限内有一点P(a,b), 且a、b是方程
的两根.若作PA⊥x轴于A,则△AOP的面积是____________.
15.请写出一个元二次方程,使它的两根之和为3,这样的方程可为___________.
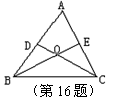16. 如图, △ABC中,D、E分别为AB、AC边的中点,DC、BE相交于点O.若△ABC的面积为6
,那么△BOC的面积为__________.
17.我市某县城为鼓励居民节约用水,对自来水用户按分段计费方式收取水费:若每月用水不超过7立方米,则按每立方米1元收费;若每月用水超过7立方米,则超过部分按每立方米2元收费. 如果某居民户今年5月缴纳了17元水费,那么这户居民今年5月的用水量为________立方米.
18.
对于整数a,b,c,d,规定
表示运算
,已知1<
<3,则
= 。
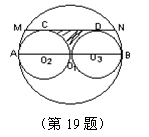
19. 如图，AB是⊙O的直径,O1A是⊙O2的直径,O1B是⊙O3的直径,AB=4,且MN与⊙O2、⊙O3相切于C、D两点,则图中阴影部分的面积是 .
三、解答题（共12分）
21. (1)计算(
－1)－1－(π－3.14)0－
+
sin450 .
(2)先化简,再选你喜爱的一个的值代入求值:
. (4分)
22.解方程
．(4分)
四、解答题(共50分)
23. (5分)已知关于
的不等式组
的整数解只有3个,试求的取值范围.
24.(5分)已知,关于x的方程
(1)当m取何值时,方程有两个不相等的实数根;
(2)设方程的两实根分别为
、
,且
,求m的值.
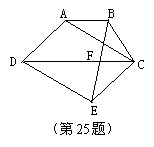25.(5分)如图,已知在梯形ABCD中,AB∥DC,以AD、AC为邻边作平行四边形ACED连结BE交DC于点F.求证:EF=BF.
26.5分)甲、乙两人在相同条件下各射靶10次,每次射靶的成绩情况如图所示.
(1)请填写下表。(2)请从下列四个不同的角度对这次测试结果进行分析.
①从平均数和方差相结合看;②从平均数和中位数相结合看(分析谁的成绩好些);
③从平均数和命中9环以上的次数相结合起来看(分析谁的成绩好些);
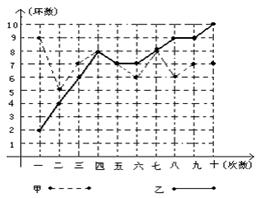④从折线图上两人射击命中环数的走势看(分析谁更有潜力)
| 平均数 | 方差 | 中位数 | 命中9环 以上次数 | |
| 甲 | 7 | 1．2 | 1 | |
| 乙 | 5．4 |
27. (6分) 江苏移动通信有限公司南通分公司新推出全球通“越打越便宜”服务,具
体优惠标准如下:
| 专项服务 | 25元 | ||
| 本地主叫 | 一分钟 | 二分钟 | 三分钟以上 |
| 0.4元/分钟 | 0.25元/分钟 | 0.15元/分钟 | |
| 本地被叫 | 接听电话免费(接听联通0.4元/分钟) | ||
(1)试写出某全球通客户某次本地主叫收费y(元)与本地主叫通话时间x(分钟)的函数关系,并求出某次本地主叫通话10分钟时的收费情况;
(2)若某全球通客户某月接听联通共计66分钟,接听本地电话共计175分钟,本地主叫30次共计345分钟,其中9次通话1分钟,6次通话2分钟,其余15次通话均在3分钟或3分钟以上,问本月此全球通客户共缴费多少元?
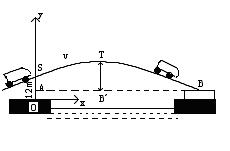
28.(8分)几年前,柯受良驾车飞越黄河的壮举令所有中国人为之骄傲.柯受良此举绝非简
单的狂热和冒险.现在请你来当一回柯受良的技术助手吧.如图,设黄河两岸处于同一水平
线上,汽车飞越的水平距离AB是41米,“起飞”的高度OS为12米,落地点B(事实上,汽车
落在一堆软箱中)的高度是4米.用电脑模拟时,可建立如图直角坐标系
,按某起飞角
度,汽车飞越的路径为抛物线
(其中
为汽车的“起飞”速度,单位:米/秒;h为常数;h、x、y的单位:米)
（1） 求h的值及起飞的速度(精确到1米/秒);
（2） 为保证飞越黄河的安全,汽车飞行的最高点T和落地点B的垂直高度差TB/不得大于10米,问:按(1)中计算出的速度起飞(起飞角度不变),能否安全飞越黄河?
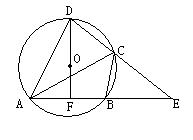
29.(8分)
已知:如图,圆内接四边形ABCD的两边AB、DC的延长线相交于点E,DF过圆心O交AB于点F,AB＝BE,连结AC,且OD＝3,AF＝FB＝
．
求AC的长．
|
30.(8分)在直角坐标系xOy中:
(1)画出一次函数y＝
x＋的图象,记作直线l,l与x轴交点为C;
(2)画△ABC,使BC在x轴上．且BC＝2,点A在直线l上且A在第一象限,∠ABC＝1200
(3)写出点A、B、C的坐标;
(4)将△ABC在直角坐标平面内旋转,使点A落在x轴上,求此时过点A、B、C的抛物线解析式.