初中毕业会考数学模拟测试（四）

初中毕业会考数学模拟测试（四）

一、填空:(每小题3分，共30分)

1．1－=________， (－x²)³÷x²=____________。

2．因式分解：a³－a=___________。

3．不等式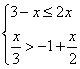的解集是_______。

4．已知y与x²成正比例，当x=－1时，y=2、则当y = 6时，x=________。

5．三角形三个内角的度数之比为1∶2∶3，最小边的长是3cm，则三角形最大边的长是________cm。

6．函数y=中自变量x的取值范围是_________。

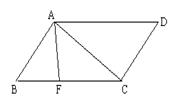
7．如图，已知平行四边形ABCD中，F为BC上一点，AB=2，AD=4，BF∶FC=1∶3，则⊿ABF与⊿ADC的面积比是________。

8．已知正三角形的边长为a，则它的内切圆与处接圆组成的圆环面积是________。

9．一次函数y=x+b的图像与x轴、y轴围成三角形的面积为4，则b=________。

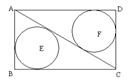10．如图，已知在矩形ABCD中，AB=6，BC=8，⊙E和⊙F分别是⊿ABC和⊿ADC的内切圆，与对角线AC分别切于E、F，则EF=_________。

二、选择:(每小题3分，共15分)

11．若(2a+3b)²=(2a－3b)²+(　 )成立，则括号内的式子是(　　)。

(A)6ab　　(B)　　24ab　　(C)12ab　　(D)18ab

12．下列四个函数中，当x>0时，随x增大而增大的函数是(　　)。

(A)　 (B)y=－2x+1　 (C)　 (D)y=－2x－1

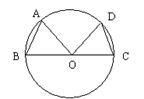
13．如图，已知在⊙O中，BC是直径，= ，∠AOD=80⁰，则　∠ABC等于(　　)。

(A)40⁰(B)65⁰ (C)100⁰(D)105⁰　　

14．当0＜x＜1时，化简的结果是　(　　)。

　 (A)　－2x　　(B)　　(C)2x　　(D)

15．半径为1cm的两个圆外切，能与这两个圆都相切，且半径为2cm的圆共有(　　)。

(A)　　5个　　(B)4个　　(C)3个　　(D)2个

三、　　 解答与作图:(共55分)

16．(5分)计算：.

17．(6分)先化简下面代数式，再求值：其中.

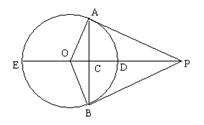18．(6分)如图，已知PA、PB是⊙O的两条切线，A、B为切点，直线OP交⊙O于点D、E，交AB于C，请你根据已知条件，写出图中五个成立的结论.(半径相等除外)

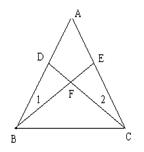
19．(6分)如图，已知：⊿ABC中，∠1=∠2，且AE=AD，BE和CD相交于F。求证：BF=CF。

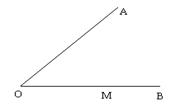20．(6分)已知∠AOB和OB上点M，求作：⊙P，使它与OA、OB都相切，且与OB的切点为M。（要求尺规作图，保留作图痕迹，并写出作法）

21．(6分)解方程：

22．(6分)已知一元二次方程x²+2x+m=0的两个实根为x₁、x₂，且，求m的值。

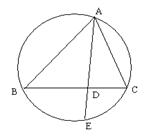23．(6分)如图，已知∠BAC的平分线与⊿ABC的边BC和外接圆分别相交于D、E。

求证：AB·AC=AD·AE.

24．(8分)列方程解应用题：

甲、乙两件服装的成本共500元，商店老板为获取利润，决定将甲服装按50%的利润定价，乙服装按40%的利润定价。在实际出售时，应顾客要求，两件服装均按9折出售，这样商店共获利157元，求甲、乙两件服装的成本各是多少元？

四、附加题（每题10分，共20分）

25．(10分)如图，已知AB是⊙O的直径，过⊙O上的点C的切线交AB的延长线于E，

AD⊥EC于D且交⊙O于F。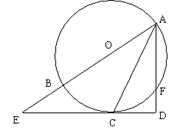⑴求证：AD+DF=AB；⑵若CE=，EB=，求⊿ADE的面积。

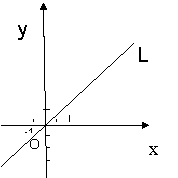
26．(10分)如图，在平面直角坐标系中，直线L的解析式为，关于x的一元二次方程2x²-2(m+2)x+(2m+5)=0(m>0)有两个相等的实数根。

（1）试求出m的值，并求出经过点A（0，-m）和点D（m，0）的直线解析式；

（2）在线段AD上顺次取两点B、C，使AB=CD=-1，使判断△OBC的形状；

（3）设直线L与直线AD交于点P，图中是否存在与△OAB的三角形？如果存在，请直接写出；如果不存在，请说明理由。