初中毕业会考数学模拟测试（五）

初中毕业会考数学模拟测试（五）

一、填空题（10小题，共30分）

⒈如果(－2) ⁿ 是一个负数，则(－1)¹＋(－1)²＋…(－1) ⁿ＋1 =　　　　　　　　　 ;

⒉已知等腰三角形中，底边长20，面积为，则其底角的正切值为　　　 ；

⒊⊙O中，弦AB、AC分别是圆内接正三边形和正六边形的边，则∠BAC =　　　　　　  ；⒋已知，则=　　　　 ；

⒌已知两圆的圆心距为8，两圆的直径分别是x ²－16x＋1 = 0的两个根，则这两圆位置关系为　　　　；

⒍若a、b满足4a ² ＋12a＋b ²－2b＋10 = 0，则y = x ^2a＋4b ＋b＋2是　　　　 函数；

⒎反比例函数的图像在第一、三象限，则m= 　　　 ；

⒏抛物线y = x² －(m－4)x－m与x轴的两交点关于y轴对称，则其顶点为　　　　　　 ；⒐在离树10米处用测角仪测得树顶的仰角为30°，测角仪高1.5米，则树高　　　　　  ；⒑三角形的边a、b满足，则其最大边c的取值范围为　　　 ；

二、选择题（10小题，共30分）

⒈若= 153.6， = 1.536，则x为（　　　　），

A、2360　　　　　　　 B、23600　　　　　　　C、23.6　　　　 D、2.36　

⒉下列关系成立的是（　　　　）

A、　<<　　　　　　　　　　　　 B、<<

C、<<　　　　　　　　　　　　　 D、<<

⒊若分式的值不为0，则（　　　　）

A、x≠2　　　　　　　 B、x≠±2　　　　　　C、x ≠- 4　　　　　 D、x≠±2且x≠ - 4

⒋已知圆锥的轴与母线的夹角是30°，底面圆的半径是1，则它的表面积是（　　　　）

A、π　　　　　　　　　 B、2π　　　　　　　　 C、3π　　　　　　　　 D、4π

⒌若多项式(x ² ＋px＋2)(x－q)不含关于x的二次项，则p与q的关系为（　　　　）

A、相等　　　　　　　 B、互为相反数　　 C、互为倒数　　　　D、乘积等于－1

⒍一台微波炉成本价是a元，销售价比成本价增加22%，因库存按销售价的60%出售，

则每台微波炉的实际售价为（　　　　）

A、a(1＋22%)(1＋60%)　　　　　　 B、a(1＋ 22%)60%

C、a(1＋22%)(1－60%)　　　　　　 D、a(1＋22%＋60%)

⒎如果圆外切等腰梯形的中位线长为5，梯形两底长的差为6，则圆的直径为（　　　　）

A、1　　　　　　　　　　 B、2　　　　　　　　　　 C、3　　　　　　　　　　 D、4

⒏已知BE、CF是锐角△ABC的两条高，且S_△ABC = 36，S_△AEF = 16，则cosA（　　　　）

A、 　　　　　　　　 B、　　　　　　　　　 C、　　　　　 D、  或

⒐下面图形中，不可能是一次函数y = mx－(m－3)的图像的是（　　　　）

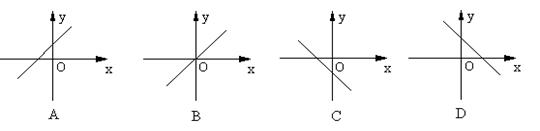
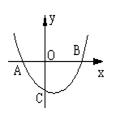⒑二次函数y = ax ²＋bx＋c的图像如图，且OA = OC，则下列结论正确的有（　　　　）

①abc＜0；②4ac－b 2＜0；③ac＋b＋1 = 0；④OA·OB = －

A、4个　　　　 B、3个　　　　　C、2个　　　　 D、1个

三、证明：（8分）

四、已知一个二次函数图像的顶点坐标为(3，－2)，且图像与x轴两交点间的距离为4，求此二次函数。（8分）

五、某厂今年一月份生产甲种机床64台，乙种机床若干台，从二月份起，甲种机床的增加率每月相同，乙种机床每月增加6台，已知二月份生产的甲种机床是乙种机床的4倍，三月份甲、乙两种机床共生产105台，求甲种机床的增加率及一月份生产乙种机床的台数。（8分）

六、如图，M（1，4）是反比例函数y = 上一点，直线y = kx＋b和双曲线y = 交

于P、Q两点，与x轴、y轴交于C、D两点，（8分）

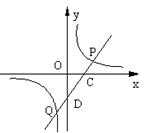① 求k的值；② 当b = －2时，求S_△COD和S_△OPQ　

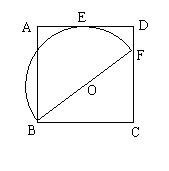
七、如图，正方形ABCD中，F在CD上，O是BF中点，以BF为直径的半圆与AD切于点E。①求证：E是AD中点。②设BF = 5，求正方形ABCD的边长。（8分）

附加题（每题10分，共20分）

⒈如图，已知以△ABC的BC边为直径的半圆交AB于D，交AC于E，　　

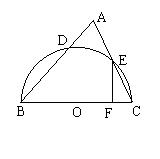 EF⊥BC于F，且BF = 5OF，AB = 8，AE = 2，求AD的长。

⒉已知如图，抛物线y = －x ² ＋4(m－1)x＋2m＋1交x轴的负半轴于A，正半轴于B。线段OA与OB的乘积等于5。

①　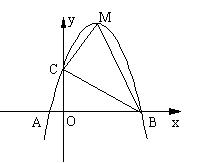　 求抛物线；②设①中抛物线的顶点为M，交y轴于C，求S_△BCM。