初中毕业会考数学模拟测试（一）
一、选择题（本大题共10个小题；每小题3分，共30分.）
1. 
的值是 ( )
A．
B．
C．
D．
2．已知数轴上的A点到原点的距离为2，那么在数轴上到A点的距离是3的点所表示的数有 ( )
A . 1个 B .2个 C.3个 D4个
3. 下列计算中，正确的是 ( )
A．2a+3b=5ab B．a·a3=a3 C．a6÷a2=a3 D．(-ab)2=a2b2
4. 第五次全国人口普查结果显示，我国的总人口已达到1 300 000 000人，用科学记数法表示这个数，结果正确的是.( )
A．1.3×108 B．1.3×109 C．0.13×1010 D．13×109
5. 如图2，天平右盘中的每个砝码的质量都是1g，则物体A的质量m(g)的取值范围，在数轴上可表示为 ( )
 | |||||||||
 | |||||||||
 | |||||||||
 | |||||||||
 | |||||||||
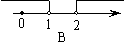6.
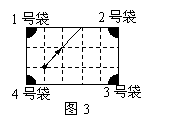图3是一个经过改造的台球桌面的示意图，图中四个角上的阴影部分分别表示四个入球孔.如果一个球按图中所示的方向被击出（球可以经过多反射），
那么该球最后将落入的球袋是.( )
A．1 号袋 B．2 号袋
C．3 号袋 D．4 号袋
7. 小明把自己一周的支出情况，用图4所示的统计图来表示，
下面说法正确的是( )
A．从图中可以直接看出具体消费数额
B．从图中可以直接看出总消费数额
C．从图中可以直接看出各项消费数额占总消费额的百分比
D．从图中可以直接看出各项消费数额在一周中的具体变化情况
8. 把一个小球以20m/s的速度竖直向上弹出，它在空中的高度h(m)
与时间t(s)满足关系：h=20t-5t2.当h=20时，小球的运动时间为 ( )
A．20s; B．2s; C．
; D．
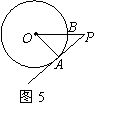
9. 如图5，PA为⊙O的切线，A为切点，PO交⊙O于点B，PA=4， OA=3，则cos∠APO的值为.( )
A．
B．
C．
D．
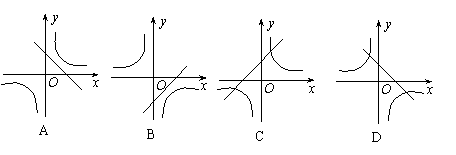10. 在同一直角坐标系中，函数y=kx-k与
(k≠0)的图象大致是( )
二、填空题（本题共6个小题；每题4分，共24分.）
11. (-3)2-1= .
12.
函数
的自变量x的取值范围是 .
13.
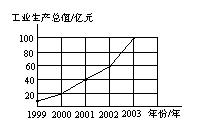
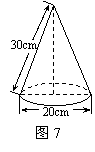图6是根据某市1999年至2003年工业生产总值绘制的折线统计图.观察统计图可得：增长幅度最大的年份是 年，比它的前一年增加 亿元.
14. 图7是小明制作的一个圆锥形纸帽的示意图.围成这个纸帽
的纸的面积为 cm2(π取3.14).
15. 在关于x1，x2，x3的方程组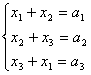
中，已知
，
那么将x1，x2，x3从大到小排起来应该是____________.
16. 扑克牌游戏：小明背对小亮，让小亮按下列四个步骤操作：
第一步 分发左、中、右三堆牌，每堆牌不少于两张，且各堆牌现有的张数相同；
第二步 从左边一堆拿出两张，放入中间一堆；
第三步 从右边一堆拿出一张，放入中间一堆；
第四步 左边一堆有几张牌，就从中间一堆拿几张牌放入左边一堆.
这时，小明准确说出了中间一堆牌现有的张数.你认为中间一堆牌现有的张数是 .
三、解答题（本大题共10个小题；共66分）
17. （本小题满分6分）当
时，求
的值.
18. （本小题满分5分）
已知，如图8，AB和DE是直立在地面上的两根立柱.AB=5m，某一时刻AB在阳光下的投影BC=3m.（1）请你在图8中画出此时DE在阳光下的投影；
（2）在测量AB的投影时，同时测量出DE在阳光下的投影长为6m，请你计算DE的长.
19. （本小题满分5分）
观察下面的点阵图和相应的等式，探究其中的规律：
（1）在④和⑤后面的横线上分别写出相应的等式；
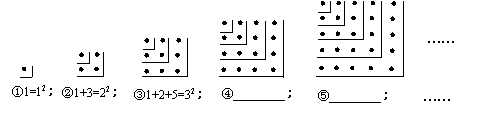
（2）通过猜想写出与第n个点阵相对应的等式____________________________.
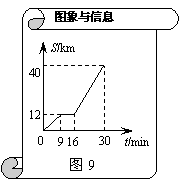
20. （本小题满分6分）图9是某汽车行驶的路程S(km)与时间t(min)的函数关系图.观察图中所提供的信息，解答下列问题：（1）汽车在前9分钟内的平均速度是多少？
（2）汽车在中途停了多长时间？（3）当16≤t≤30时，求S与t的函数关系式.
| 印数a (单位：千册) | 1≤a＜5 | 5≤a＜10 |
| 彩色 (单位：元/张) | 2．2 | 2．0 |
| 黑白（单位：元/张） | 0．7 | 0．6 |
21. （本小题满分6分）某中学为筹备校庆活动，准备印制一批
纪念册。该纪念册每册需要10张8K大小的纸，其中4张为彩页，6张为黑白页。印制该纪念册的总费用由制版费和印刷费两部分组成，制版费与印数无关，价格为：彩页300元/张，黑白页50元/张；印刷费与印数的关系见下表（1）印制这批纪念册的制版费为 元；（2）若印制2千册，则共需多少费用？
（3）如果该校希望印数至少为4千册，总费用至多为60 000元，求印数的取值范围。
22. （本小题满分8分）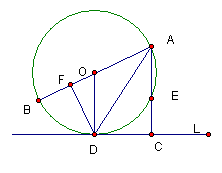
如图，以知AB为⊙O的直径，直线L与⊙O相切于点D，AC⊥L，垂足为C，AC交⊙O于点E，DF⊥AB，垂足为F。
（1） 图中哪条线段与BF相等？试证明你的结论。
（2） 若AE=3，CD=2，求⊙O的直径。
23. （本小题满分10分）
用两个全等的等边三角形△ABC和△ACD拼成菱形ABCD.把一个含60°角的三角尺与这个菱形叠合，使三角尺的60°角的顶点与点A重合，两边分别与AB，AC重合.将三角尺绕点A按逆时针方向旋转.
（1）当三角尺的两边分别与菱形的两边BC，CD相交于点E，F时，（如图13—1），通过观察或测量BE，CF的长度，你能得出什么结论？并证明你的结论；
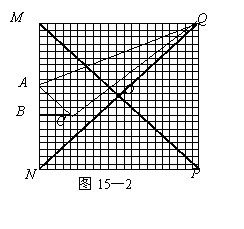
（2）当三角尺的两边分别与菱形的两边BC，CD的延长线相交于点E，F时（如图13—2），你在（1）中得到的结论还成立吗？简要说明理由.
24. （本小题满分10分）
如图14—1是某段河床横断面的示意图.查阅该
河段的水文资料，得到下表中的数据：
| x/m | 5 | 10 | 20 | 30 | 40 | 50 |
| y/m | 0.125 | 0.5 | 2 | 4.5 | 8 |
|
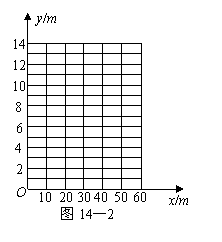
12.5（1）请你以上表中的各对数据（x，y）作为点的坐标，
尝试在图14—2所示的坐标系中画出y关于x的
函数图象；
（2）①填写下表：
| x | 5 | 10 | 20 | 30 | 40 | 50 |
|
|
②根据所填表中数据呈现的规律，猜想出用x表
示y 的二次函数的表达式： .
（3）当水面宽度为36米时，一艘吃水深度（船底部到水面的距离）为1.8米的货船能
否在这个河段安全通过？为什么？
25. （本小题满分10分）
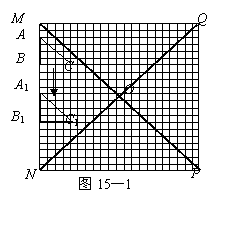
如图15—1和15—2，在20×20的等距网格（每格的宽和高均是1个单位长）中， Rt△ABC从点A与点M重合的位置开始，以每秒1个单位长的速度先向下平移，当BC边与网的底部重合时，继续同样的速度向右平移，当点C与点P重合时，Rt△ABC停止移动.设运动时间为x秒，△QAC的面积为y.
（1）如图15—1，当Rt△ABC向下平移到Rt△A1B1C1的位置时，请你在网格中画出Rt△A1B1C1关于直线QN成轴对称的图形；
（2）如图15—2，在Rt△ABC向下平移的过程中，请你求出y与x的函数关系式，并说明当x分别取何值时，y取得最大值和最小值？最大值和最小值分别是多少？
（3） 在Rt△ABC向右平移的过程中，请你说明当x取何值时，y取得最大值和最小值？最大值和最值分别是多少？为什么？
 | |||
 | |||