初三数学
第一学期期末考试试卷
（满分：150分；考试时间：120分钟） 得分___________
一、选择题（每小题3分，计36分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
1. 点P（2，－1）关于
轴对称点Q的坐标为
A. （－2，－1） B. （2，1） C. （－2，1） D. （－1，2）
2. 已知：正比例函数
中，
随的增大而减小，则
A.
＜
B.
＞ C.
＜且≠0 D. ＞2
3. 已知：⊙O中，直径AB＝4，弦CD⊥AB于E点，且OE＝
，则弦CD的长为
A.
1 B.
D. 2
4. 已知：与－1成反比例，且＝2时，＝－1，则关于的函数关系为
A. 
B.
C.
D.
5. 已知：⊙O的外切梯形的中位线长为10
，则该梯形的周长为
A.
40 B.
20 C.
30 D.
45
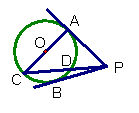
6. 已知：如图，A、B、C在⊙O上，点D在AB延长线上，
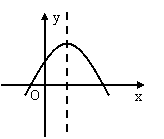且∠AOC＝110°，则∠CBD等于
A. 45° B. 50° C. 55° D. 65°
7. 某班七个学习兴趣小组人数如下：5、5、6、、7、7、8，已知
这组数据的平均数为6，则这组数据的中位数是
A. 7 B. 6 C. 5.5 D. 6.5
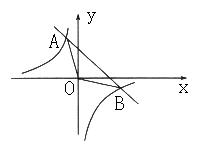
8. 二次函数
的图象如图，则点M（
，
）在
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
9. 小强家最近装修房子，选了正三角形地砖铺地面，发现花样太单调，决定再买一
种边长与正三角形边长相等的正多边形进行平面镶嵌，以下几种正多边形中，不
能选的正多边形为
A. 正方形 B. 正八边形 C. 正六边形 D.正十二边形
10. 秋千拉绳长2米，静止时踩板离地面0.5米，某小朋友荡秋千时，秋千在最高处
踩板离地面1.5米（左、右对称），则该秋千中一根绳子所荡过的扇形的面积为
A. 
B.
C.
D.
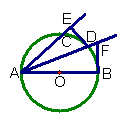
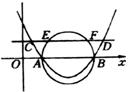11. 抛物线过点A（2，0），B（6，0），C（1，），平行于轴
的直线CD交抛物线于点C、D，以AB为直径的圆交直线CD于
点E、F（如图），则CE＋FD的值是
A. 2 B.
4 C.
5 D.
2
12. 已知：两圆的圆心距
＝4，它们的半径是一元二次方程
的两根，则
它们的公切线有
A. 0条 B. 1条 C. 2条 D. 3条
二、填空题（每小题4分，计32分）
13. 函数
的自变量的取值范围为____________.
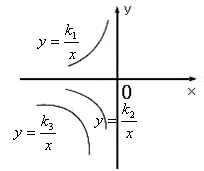14. 如果点A（－3，
）在直线
上，则点A到轴的距离为_________.
15. 已知：三个反比例函数
在轴左侧的图象如图所示，则
的大
小关系为_______________.
16. 已知：正六边形的面积为6，则它的内切圆与外接
圆所组成的圆环面积为______________。（结果保留
）
17. 已知：
、
、
……
是直线
上的点，且
的方差为8，则
的方差为_____________.
18. 二次函数
与轴的两个交点，以及抛物线的顶点构成等边三角
形，且开口向上，则它的解析式为__________________.
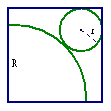
19. 如图，在正方形铁皮上剪下一个圆形和一个扇形，
使之恰好围成一个圆锥模型，设圆的半径为
，
扇形半径为R，则圆的半径与扇形半径之间的函
数关系为______________________.
20. 已知：如图，PA、PB与⊙O分别相切于A、B点，AC为
⊙O的直径，PC交⊙O于D，且∠APB＝60°，AC＝2，
则CD＝___________.
三、解答题
21.（本题满分8分）
已知：如图，一次函数
的图象与反比例函数
的图象交于A、B
两点，且点A的横坐标与点B的纵坐标都是－2，
求：（1）一次函数解析式；
（2）△AOB的面积。
22.（本题满分8分）
已知：如图，⊙O中，AB为直径，半径为R，且AC＝
R，
（1）求∠AOC的度数；
（2）若D为劣弧BC上的动点，且弦AD交半径OC于E，
试探求△AEC≌△DEO时，D点的位置。
23.（本题满分8分）
已知：二次函数的关系如下表：
|
| －1 |
| 0 |
| 1 | 2 |
|
| 0 |
| －4 |
| －6 | －6 |
－
（1）求二次函数的解析式；
（2）在何范围内时，＜0？
24.（本题满分10分）
已知：如图，AB为⊙O的直径，D是BC的中点，DE⊥AC
交AC延长线于E，⊙O的切线BF交AD延长线于F，
（1）求证：DE是⊙O的切线；
（2）若DE＝3，⊙O的半径为5，求BF的长。
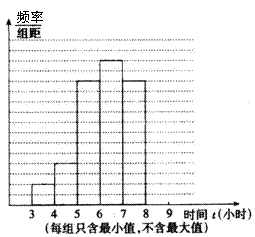
25.（本题满分10分）某校课外活动小组为了解本校初三学生睡眠时间情况，对学校
若干名初三学生的睡眠时间进行了抽样调查，所得数据整理后，画出了频率分布
直方图的一部分（如图），已知从左到右前五个小组的频率分别为0.04，0.08，0.24，
0.28，0.24，第二小组的频数为4，请回答：
（1）这次被抽查的学生人数是多少？并补全频率分布直方图；
（2）被抽查的学生中，睡眠时间在哪个范围内的人数最多？这一范围内的人数是
多少？
（3）如果该校有900名初三学生，若合理睡眠时间范围为7≤
＜9，那么请你估
计一下这个学校初三学生中睡眠时间在此范围内的人数是多少？
26.（本题满分12分）润扬机械设备有限公司生产某种产品，每件产品的出厂价为100
元，其原材料成本价（含设备损耗等）55元，同时生产过程中平均每生产一件产品
有2吨的废渣产生，为了达到国家环保要求，需要对废渣进行脱硫、脱氮等处理，
现有两种方案可供选择：
方案一：由公司对废渣直接处理，每处理1吨废渣所用原料费为5元，并且每月设
备维护及损耗费为2000元；
方案二：公司将废渣集中到废渣处理厂统一处理，每处理1吨废渣需付10元处理费；
问：（1）设备公司每月生产件产品，方案一的月利润为
，方案二的月利润为
，
分别求出、与之间的函数；
（2）若你作为公司负责人，如何根据月生产量选择处理方案，既可达到环保要
求又最合算？
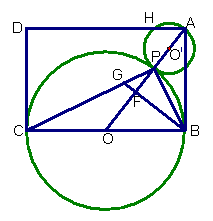
27.（本题满分12分）已知：如图，矩形ABCD，以BC为直径作⊙O交AO于P，连PC、
PB，过B作BF⊥AO于F交PC于G，
（1）求证：PB2＝PG·PC；
（2）若PF＝
，
∠OAB＝
，求OA的长；
（3）在（2）的条件下，若以AP为直径的⊙O′交AD于H，求AH:HD的值。
28.（本题满分14分）已知抛物线
开口向下，与轴交于
A（
，0）和B（
，0）两点，（其中＜）
（1）求
的取值范围；
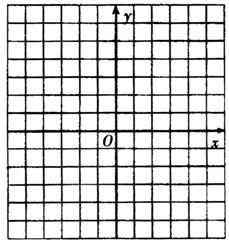
（2）若OA·OB＝3，求抛物线的解析式，并在给出的直角坐标系中画出抛物线的草
图；
（3）在（2）的条件下，设抛物线的顶点为C，延长CA交轴于点D，在轴上是
否存在点P，使以P、O、B为顶点的三角形与△BCD相似？若存在，直接写出P
点的坐标，若不存在，请说明理由；
（4）在（3）的条件下，连OC，求△COD外接圆的半径。