初三数学模拟试卷A
一、选择题(本题共有10个小题,每小题4共40分)
1.-![]() 的绝对值是
的绝对值是
A.-![]() B.
B.![]() C.5 D.-5
C.5 D.-5
2.下列运算正确的是
A.a2+a3=a5
B.(-2x)3=-2x3
C.(a-b)(-a+b)=-a2-2ab-b2
D.![]()
3.南京长江三桥是世界上第一座弧线形钢塔斜拉桥.全长15600m,用科学记数法表示为
A.1.56×104m B.15.6×103 m C.0.156×104m D.1.6×104m
 4.下列图形既是轴对称图形,又是中心对称图形的是
4.下列图形既是轴对称图形,又是中心对称图形的是
5.两圆的半径R、r分别是方程x2-3x+2=0的两根,且圆心距d =3,则两圆的位置关系为
A.外切 B.内切 C.外离 D.相交
6. 抛物线![]() 的顶点坐标是( ).
的顶点坐标是( ).
A.(0,-2) B.(-2,0) C.(0,2) D.(2,0)
7577.不等式组![]() 的正整数解的个数是
的正整数解的个数是
A.1个 B.2个 C.3个 D.4个
8.一根蜡烛经凸透镜成一实像,物距u,像距v和凸透镜的焦距f满足关系式:+ = .若u =12㎝,f =3㎝,则v的值为
A.8㎝ B.6㎝ C.4㎝ D.2㎝
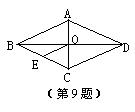
9.已知:如图,菱形ABCD中,对角线AC与BD相交于点O,
OE∥DC交BC于点E,AD=6cm,则OE的长为 ( )
A、6 cm B、5 cm
C、4 cm D、3 cm
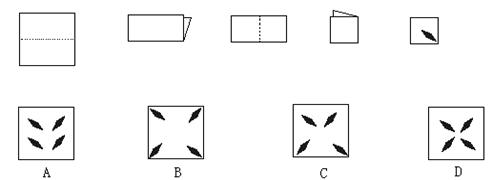
10.如图,将一张正方形纸片经两次对折,并剪出一个菱形小洞后展开铺平,得到的图形是( )
![]()
二、填空题(本题共有6个小题。每小题5分共30分)
11.、函数y=![]() 中,自变量x的取值范围是_________________
中,自变量x的取值范围是_________________
12.在实数内分解因式:x4-4x2= .
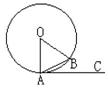
13.如图,A、B是⊙O上的两点,AC是⊙O的切线,∠B=65º,则∠BAC=______________
14.袋中有5个黑球,3个白球和2 个红球,球的形状.大小都一样.那么摸出红球的概率为__________.
15.如果圆柱的母线长为5cm,底面半径为2cm,那么这个圆柱的侧面积是____________
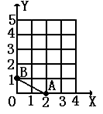
16.如图,在网络交点上找一点C,使ΔOAB与由A、B、C三点构成的三角形相似,但不全等,则C点坐标可以是 。(网络不能扩大)
 .
.
|
|
三、解答题(本题有8个小题80分)
17.(本题8分)(1)计算:![]() ;
;
(2)解方程
![]()
18.(本题8分)如图,平行四边形ABCD中,AE⊥BD,CF⊥BD,垂足分别为E、F。
(1) 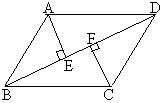 写出图中你认为全等的一对三角形_____________________
写出图中你认为全等的一对三角形_____________________
(2) 并加以证明。
19.(本题8分)
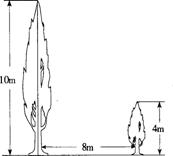
如图,有两棵树,一棵高10米,另一棵高4米,两树相距8米. 一只小鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行多少米?
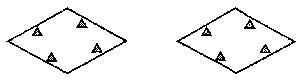
20.(本题8分)如图,菱形公园内有四个景点,请你用两种不同的方法,按下列要求设计成四个部分:⑴用直线分割;⑵每个部分内各有一个景点;⑶各部分的面积相等。(可用铅笔画,只要求画图正确,不写画法)
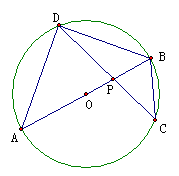
21.(本题10分)已知如图AB为⊙O直径,弦DC交AB于P。
(1)求证:ΔAPD∽ΔCPB;
(2)若 BD=BO,求:sinC 的值.
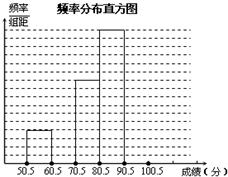
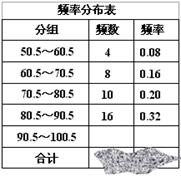
22.(本题12分)为了让学生了解环保知识,增强环保意识,红星中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题:
(1)填充频率分布表中的空格; (2)补全频率分布直方图;
(3)全体参赛学生中,竞赛成绩落在哪组范围内的人数最多?答: 。
 (4)若成绩在90分以上(不含90分)为优秀,则该校成绩优秀的约为多少人?答:
。
(4)若成绩在90分以上(不含90分)为优秀,则该校成绩优秀的约为多少人?答:
。
 |
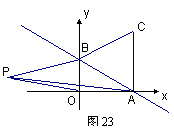 23.(本题12分).如图12,一次函数
23.(本题12分).如图12,一次函数![]() 的图象与
的图象与![]() 轴、
轴、![]() 轴分别交于点A、B,以线段AB为边在第一象限内作等边△ABC,
轴分别交于点A、B,以线段AB为边在第一象限内作等边△ABC,
(1) 求△ABC的面积;
(2) 如果在第二象限内有一点P(![]() ),试用含
),试用含![]() 的式
的式
子表示四边形ABPO的面积,并求出当△ABP的面
积与△ABC的面积相等时![]() 的值;
的值;
(3) 在![]() 轴上,存在这样的点M,使△MAB为等腰三角形.
轴上,存在这样的点M,使△MAB为等腰三角形.
请直接写出所有符合要求的点M的坐标.
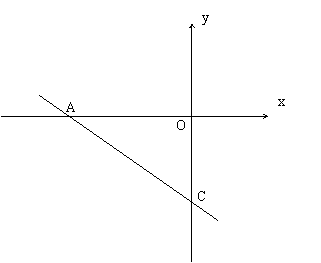
24、(14分)函数y=-![]() 的图象分别交x轴,y轴于A,C两点,
的图象分别交x轴,y轴于A,C两点,
(1) 求出A、C两点的坐标。
(2) 在x轴上找出点B,使ΔACB∽ΔAOC,若抛物线经过A、B、C三点,求出抛物线的解析式。
 (3)在(2)的条件下,设动点P、Q分别从A、B两点同时出发,以相同的速度沿AC、BA向C、A运动,P到C时整个运动过程结束,连结PQ,设AP=m,是否存在m值,使以A、P、Q为顶点的三角形与ΔABC相似,若存在,求出所有的m值;若不存在,请说明理由。
(3)在(2)的条件下,设动点P、Q分别从A、B两点同时出发,以相同的速度沿AC、BA向C、A运动,P到C时整个运动过程结束,连结PQ,设AP=m,是否存在m值,使以A、P、Q为顶点的三角形与ΔABC相似,若存在,求出所有的m值;若不存在,请说明理由。