初三数学上学期第一次月考试题
时间：120分钟 分值：150分
第Ⅰ卷（选择题 共48分）
一、选择题：（每小题4分，共48分）
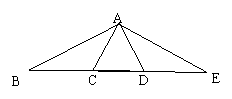
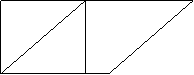
1、把两个一样大的含30°的直角三角板，按如图方式拼在一起，
其中等腰三角形有（ ）
A、1个 B、2个 C、3个 D、4个
2、到三角形三边距离相等的点是（ ）
A、三条中线的交点 B、三条高线的交点
C、三条角平分线的交点 D、不确定
3、关于x的方程（m－2）x│m│+3mx+1＝0是一元二次方程，则m的值为（ ）
A、m＝±2 B、m＝2 C、m＝－2 D 、m≠±2
4、下列方程中，是一元二次方程的是（ ）
A、
+
－2＝0 B、3（m+1）2 ＝2(m+1)
C、ax+bx+c＝0 D、n2+2n＝n2－1
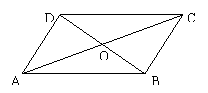5、如图，ABCD中，对角线AC和BD相交于点O，如果AC＝14，
BD＝10，AB＝m，那么m的取值范围是（ ）。
A、10< m<14 B、4< m<24
C、2< m<12 D、5< m<7
6、某钢铁厂今年1月份钢产量为4万吨，三月份钢产量为4.84万吨，每月份的增长率相同，问2、3月份平均每月的增长率是（ ）
A、7℅ B、8℅ C、9℅ D、10℅
7、一个小组有若干人，新年互送贺年片一张，已知全组共送贺年片90张，则这个小组共有（ ）
A、9人 B、9或10人 C、10人 D、不能确定
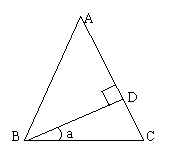
8、如图，△ABC中，AB＝AC，BD⊥AC于D，
则∠a与∠A的关系是（ ）
A、∠a ＝
∠A B、∠a ＝∠A
C、∠a ＝90°－∠A D、∠a ＝90°－∠A
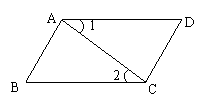9、如图，在四边形ABCD中，AB＝CD，要使AD＝BC
只要（ ）
A、∠1＝∠2 B、∠BAC＝∠DCA
C、∠B＝∠D D、AB＝AD
10、顺次连接等腰梯形各边中点所得的四边形一定是（ ）
A、梯形 B、矩形
C、菱形 D、正方形
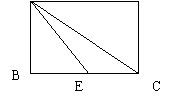11、如图，矩形ABCD中E为BC的中点，∠BAE＝30° A D
AE＝2，则AC等于（ ）
A、3 B、2
C、
D、
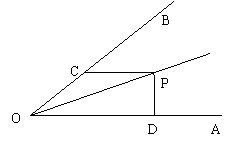12、如图，∠AOP＝∠BOP＝15°，PC∥OA，PD⊥OA，
若PC＝4，则PD等于（ ）
A、1 B、2 C、3 D、4
一、选择题答案：
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
第Ⅱ卷（非选择题 共102分）
二、填空题：（共5个小题，每小题4分）
1、在△ABC中，∠A、∠B、∠C的对边分别为a、b、c，若∠B＝60°，且满足条件
a2－2ac+c2＝0，则△ABC的形状是＿＿＿＿＿＿＿＿。
2、方程（x+2）（x－2）＝x－2的解是＿＿＿＿＿＿＿＿。
3、用配方法把一元二次方程x2－2x－5=0化成（x+a）2＝b的形式为＿＿＿＿＿则此方程的根为＿＿＿＿。
4、一等腰三角形腰长为4cm，腰上的高为2cm，则等腰三角形的顶角为＿＿＿＿＿。
5、如图，以正方形ABCD的对角线AC为一边， D C F
延长AB到E，使AE＝AC，以AE为一边
作菱形AEFC，若菱形的面积为16，
则正方形的边长＿＿＿＿＿＿。 A B E
三、解答题：（本题共8小题，共82分）
1、解方程：（本题共4小题，共20分）
① 3x(x+2)＝5x+10 ② (x－1)(x+2)＝70
③ －3x2－4x+4＝0 ④ 2x2－4x－5＝0
 |
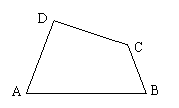2、（6分）如图，已知四边形ABCD，求做一点P，
使点P到AB、AD的距离相等，且PD＝PC。
（不写作法，保留作图痕迹）
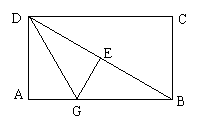3、（10分）折叠矩形纸片ABCD，先折出折痕BD，再折使AD边与对角线BD重合，得折痕DG，如图，若AB＝2，BC＝1，求AG。
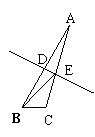4、（10分）如图所示，在△ABC中，AB的垂直平分线交AB于D，交AC于点E，△ABC的周长为76，BD＝8，求△BCE的周长。
5、（12分）如图所示，要建一个面积为130m2的仓库，仓库有一边靠墙（墙长16 m），并在与墙平行的一边开一道宽1m的门，现有能围成32 m的木板，求仓库的长与宽？
 |
6、（12分）某种商品，按标价销售每件可盈利50元，平均每天销售24件，根据市场信息，若每件降价2元，则每天可多销售6件，如果经销商想保证每天盈利2160元，同时考虑不过分增加营业员的工作量，每件应降低多少元？
7、（12分）阅读下题及其证明过程：
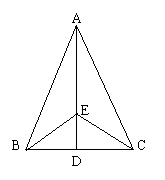已知：如图，D是△ABC中BC边上一点，EB＝EC，
∠ABE＝∠ACE，求证：∠BAE＝∠CAE
证明：在△AEB和△AEC中，
EB＝EC
∠ABE＝∠ACE
AE＝AE
∴△AEB≌△AEC （第一步）
∴∠BAE＝∠CAE （第二步）
问：上面证明过程是否正确？若正确，请写出每一步推理根据；若不正确，请指出错在哪一步？并写出你认为正确的推理过程。