初三数学上学期年期中试卷

初三数学上学期年期中试卷　

 班级　　　　  　 姓名　　　　　　　　　　　　　　　　　　　　

一、选择题：（本题共10小题，每题3分，共30分）　　　　　　

1、已知⊙O₁的半径是3，⊙O₂的半径是4，O₁O₂=8，则这两圆的位置关系是

　 A、相交　　　　  B、相切　　　　C、内含　　　　　 D、外离

2．若抛物线y=a(x-k)²+h的开口向下，顶点是（1，3），y随x的增大而减小，则x的取值范围是（ 　）

（A）x＞3； （B）x＜3； （C）x＞1；　（D）x＜1。

3、一等腰直角三角形的内切圆与外接圆的半径之比为（　　）

　　A、　　B、　　C、＋1　　　D、－1

4．在同一时刻的阳光下，小明的影子比小强的影子长，那么在同一路灯下（　　 ）

A．小明的影子比小强的影子长　　  B.小明的影长比小强的影子短

C.小明的影子和小强的影子一样长　 D.无法判断谁的影子长

6．若反比例函数的图象经过（2，-2），（m，1）,则m=（　　　）

A．　1　　　 B．　 -1　　　　C．　 4　　　D．　 -4

7．如图，两个同心圆中，大圆的半径是小圆半径的2倍，把一粒

大米抛到圆形区域中，则大米落在小圆内的概率为（　　　）　　　　　　　　

A． 　　　　　　B．　　　　　　　　　 

C． 　　　　　　D．无法确定

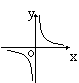
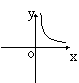
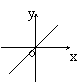
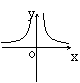
8．如果矩形的面积为6cm²，那么它的长cm与宽cm之间的函数关系用图象表示大致　（　　　）

A　　　　　　　　 B　　　　　　　　 C　　　　　　 D

9．设“○”、“□”、“△”分别表示三种不同的物体，　　　　　　　　　　　　 

用天平比较它们质量的大小，两次情况如图所示，　　　　　　　　　　 

那么每个“○”、“□”、“△”这样的物体，　　　　　　　　　　　　　　　　

按质量从小到大的顺序排列为（　　　）　　　　　　　　　　　　　　　　　　

A、○□△　  B、○△□　  C、□○△　  D、△□○　　　　　　　　 

10．某地区为估计该地区黄羊的只数，先捕捉20只黄羊给它们分别作上标志，然后放回，待有标志的黄羊完全混合于黄羊群后，第二次捕捉40只黄羊，

发现其中两只有标志。从而估计该地区有黄羊（　　　 ）

A．200只　　　　  B 400只　　　　 C800只　　　　　  D1000只

二、填空。（本题共10小题，每题3分，共30分）

11.直线y=kx+6与x轴的交点的横坐标为-3，则k的值是　　　　 ．　　

12．函数中，自变量x的取值范围是　　　 　　；函数中，

自变量x的取值范围是　　　　　 。

13．若函数的图象经过点（－1，2），则k的值是　　　 。

14、函数y=x²-2x+3的图象顶点坐标是　　　　　

15．已知⊙O₁与⊙O₂内切，它们的半径分别为2和3，则这两圆的圆心距d满足　　　　　　 

16、已知圆锥的母线长是5㎝，底面半径是2㎝，则这个圆锥的侧面积是　　 ㎝².

17、在一幅长80cm，宽50cm的矩形风景画的四周镶一条金色纸边，制成一幅矩形挂画，

设整个挂画总面积为ｙcm²，金色纸边的宽为ｘcm，则ｙ与ｘ的关系式是_________________．

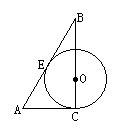
18．如图,∠C=15°，且，则∠E的度数为　　　　　　　 　　  

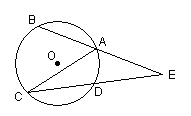19. 如图,RtΔABC中,∠C=90⁰,AC=6,BC=8,CD为直径的⊙O与AB相切于E,则⊙O的半径是　　　　　  　　 

（18　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （ 19 ）　

20、观察下表中三角形个数变化规律，填表并回答下面问题．

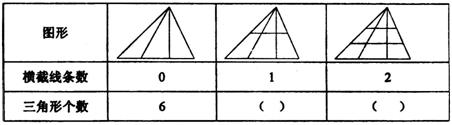
问题：如果图中三角形的个数是102个，则图中应有_______条横截线．

三、（本题共6题，，共30分）

21．（4分）如图中的图象（折线ABCDE）描述了一汽车在某一直线上的行驶过程中，

汽车离出发地的距离s（千米）和行驶时间t（小时）之间的函数关系，

根据图中提供的信息，回答下列问题：

①　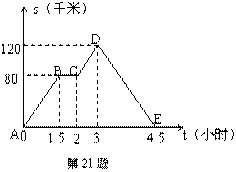　 汽车共行驶了多少千米？

②　　 汽车在行驶途中停留了几小时？

③　　 汽车在整个行驶过程中的平均速度为多少千米/时？

④　　 汽车自出发后3小时至4.5小时之间行驶的速度发生怎样的变化？（减少还是增大？）

22．（4分）三根垂直地面的木杆甲、乙、丙，

在路灯下乙、丙的影子如图所示。

试确定路灯灯炮的位置，再作出甲的影子。

（不写作法，保留作图痕迹）

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　 

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

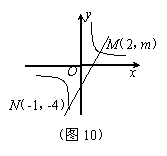
24、如图，一次函数的图象与反比例函数的图象交于M、N两点.

（1）求反比例函数和一次函数的解析式；（4分）

（2）根据图象写出使反比例函数的值大于一次函数的值的x的取值范围.（4分）

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　 

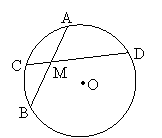
25、如图，⊙O的两弦AB、CD相交于点M，AB=8cm，M是AB的中点，CM：MD=1：4，

则弦CD的长是多少？（本题满分6分）

　

四、某影碟出租店开设两种租碟方式：一种是零星租碟，每张收费1元；另一种是会员卡租碟，

办卡费每月12元，租碟费每张0.4元 . 小彬经常来该店租碟，若每月租碟数量为x张.

（1）写出零星租碟方式应付金额y₁(元)与租碟数量x（张）之间的函数关系式；（2分）

（2）写出会员卡租碟方式应付金额y₂(元 )与租碟数量x(张)之间的函数关系式；（2分）

（3）小彬选取哪种租碟方式更合算？（4分）

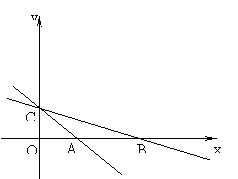五、直线y= -x+m与直线y=x+2相交于y轴上的点C，与x轴分别交于点A、B。

　（1）求A、B、C三点的坐标；（3分）

解：

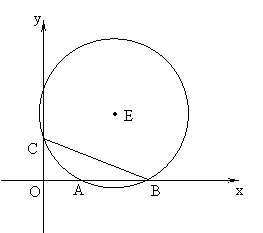（2）经过上述A、B、C三点作⊙E，求∠ABC的度数，圆心E的坐标和⊙E的半径；（7分）

解：

附加题：(可算入总分,全卷满分100分)

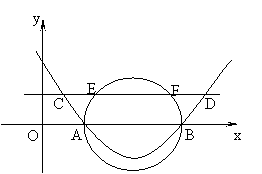
1、　如图，抛物线过点A（2，0）、B（6，0）、C（1，），

平行于x轴的直线CD交抛物线于点C、D，

以AB为直径的圆交直线CD于点E、F，

则CE+FD的值是　　　　　 (4分)

　

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　 

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

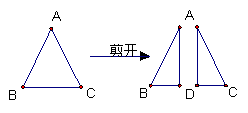
2、　如图，已知在△ABC中，AB=AC，AD⊥BC于D，且AD=BC=4，若将三角形沿AD

剪开成为两个三角形，在平面上把这两个三角形拼成一个四边形，你能拼出所有的

不同形状的四边形吗？画出所拼四边形的示意图（标出图中的直角），并分别写出

所拼四边形的对角线的长．（只需写出结果即可）