中等学校招生统一考试数学试题卷(非课改区)
注意:
1.考试时间120分钟,满分120分;
2.本试卷分为试题卷和答题卷两部分,请把答案写在答题卷上,若写在试题卷上无效.
 一、填空题:本大题共10小题,每小题2分,共20分.
一、填空题:本大题共10小题,每小题2分,共20分.
1.![]() 的相反数是_____________.
的相反数是_____________.
2.分解因式:![]() _____________.
_____________.
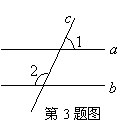
3.如图,已知直线![]() ,
,![]() ,则
,则![]() _____________.
_____________.
4.不等式组![]() 的解集是_____________.
的解集是_____________.
5.据报道:2005年全国财政收入达到![]() 亿元,用科学计数法表示为__________元(保留三个有效数字).
亿元,用科学计数法表示为__________元(保留三个有效数字).
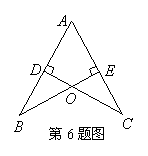 6.如图,
6.如图,![]() ,
,![]() ,请你再添加一个条件:__________,使
,请你再添加一个条件:__________,使![]() .
.
7.若反比例函数![]() 的图像经过点
的图像经过点![]() ,则
,则![]() 的值为_____________.
的值为_____________.
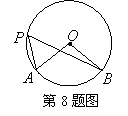 8.如图,在
8.如图,在![]() 中,
中,![]() .点
.点![]() 是优弧上一动点(不与
是优弧上一动点(不与![]() ,
,![]() 重合),则
重合),则![]() 的度数是_____________.
的度数是_____________.
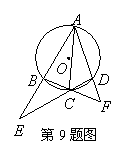 9.如图,四边形
9.如图,四边形![]() 内接于
内接于![]() ,
,![]() ,
,![]() 的延长线交于点
的延长线交于点![]() ,
,![]() ,
,![]() 的延长线交于点
的延长线交于点![]() ,请你写出图中所有的相似三角形_____________.
,请你写出图中所有的相似三角形_____________.
10.观察下面用棋子摆成的一列图案,每个图案棋子的个数记为![]() .
.
 |
按此规律,可推断出![]() 与
与![]() 的关系式为_____________.
的关系式为_____________.
二、选择题:本大题共8小题,每小题3分,共24分.在每小题给出的四个选项中,只有一项是符合题目要求的.
11.下列运算中,正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
12.某农村贫困家庭的孩子读书,今年享受“两免一补”(即免学杂费、免课本费,补助寄宿生活费),加上免收农业税,该家庭现在平均每月可减少![]() 的费用支出.若该家庭原来平均每月支出
的费用支出.若该家庭原来平均每月支出![]() 元,则现在每月的支出为( )
元,则现在每月的支出为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
13.已知关于![]() 的方程
的方程![]() 有实数根,则
有实数根,则![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
14.已知两圆的半径分别为![]() 厘米和
厘米和![]() 厘米,若圆心距为
厘米,若圆心距为![]() 厘米,那么这两个圆的公切线共有( )
厘米,那么这两个圆的公切线共有( )
A.![]() 条 B.
条 B.![]() 条 C.
条 C.![]() 条 D.
条 D.![]() 条
条
15.在四边形![]() 中,
中,![]() 是对角线交点,下列条件中,不能判定四边形
是对角线交点,下列条件中,不能判定四边形![]() 是平行四边形的是( )
是平行四边形的是( )
A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]() ,
,![]()
16.函数![]() 的自变量
的自变量![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() 且
且![]() C.
C.![]() D.
D.![]() 且
且![]()
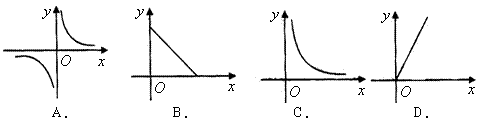 17.一块长方形花圃的面积为
17.一块长方形花圃的面积为![]() ,则它的长
,则它的长![]() 与宽
与宽![]() 之间的关系用图像大致可表示为( )
之间的关系用图像大致可表示为( )
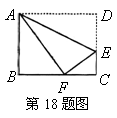
18.如图,沿![]() 折叠矩形纸片
折叠矩形纸片![]() ,使点
,使点![]() 落在
落在![]() 边的点
边的点![]() 处.已知
处.已知![]() ,
,![]() ,则
,则![]() 的值为( )
的值为( )
 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
三、解答题:本大题共9小题,满分76分.解答应写出文字说明、证明过程或演算步骤.
19.(本小题满分6分)
计算:![]() .
.
20.(本小题满分6分)
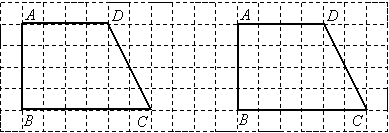 用一条直线将一个直角梯形分成面积相等的两部分,请你在下面的图中分别画出两种不同的分割图形.
用一条直线将一个直角梯形分成面积相等的两部分,请你在下面的图中分别画出两种不同的分割图形.
21.(本小题满分8分)
为了从甲、乙两名同学中选拔一个参加校运会比赛,在相同条件下对他们进行了8次体能测试,测试成绩如下:(注:成绩80分以上(含80分)为合格)
甲:60 70 75 75 80 75 80 85
乙:55 60 65 65 80 90 90 95
(1)请你根据上述提供的信息填写下表:
| 平均分 | 中位数 | 成绩合格次数 | |
| 甲 |
| ||
| 乙 |
|
|
(2)根据平均分和成绩合格次数比较,_____________的成绩较好;
根据平均分和中位数比较,_____________的成绩较好;
(3)结合所学的统计知识分析,你认为应选拔哪位同学去参赛较合适,并简述理由.
22.(本小题满分8分)
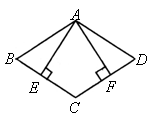 在菱形
在菱形![]() 中,
中,![]() ,
,![]() ,垂足分别为
,垂足分别为![]() ,
,![]() .
.
求证:![]() .
.
23.(本小题满分8分)
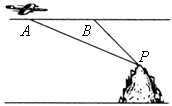 航空测量飞机在与地面平行的直线上飞行,且与一座山的山顶在同一铅垂平面内,已知飞机的飞行高度为
航空测量飞机在与地面平行的直线上飞行,且与一座山的山顶在同一铅垂平面内,已知飞机的飞行高度为![]() 米,速度为
米,速度为![]() 米/秒,飞机在点
米/秒,飞机在点![]() 处观测山顶
处观测山顶![]() 的俯角为
的俯角为![]() ,经过
,经过![]() 分钟后到达
分钟后到达![]() 处,这时观测山顶
处,这时观测山顶![]() 的俯角为
的俯角为![]() ,求山的高度.(精确到
,求山的高度.(精确到![]() 米)
米)
24.(本小题满分8分)
我市某县要在2006年通过自治区“两基”达标验收,县内一初级中学有![]() 套旧课桌椅需要修理,现有甲、乙两个木工小组都想承接这项修理业务.经商谈知:甲小组单独修理这批桌椅比乙小组多用
套旧课桌椅需要修理,现有甲、乙两个木工小组都想承接这项修理业务.经商谈知:甲小组单独修理这批桌椅比乙小组多用![]() 天;乙小组每天比甲小组多修理
天;乙小组每天比甲小组多修理![]() 套.求甲、乙两小组每天各修理桌椅多少套?
套.求甲、乙两小组每天各修理桌椅多少套?
25.(本小题满分10分)
某水果店为了尽快销售一种水果,按以下方法进行促销:购买这种水果不超过![]() 千克的,每千克
千克的,每千克![]() 元;超过
元;超过![]() 千克的,超出部分每千克
千克的,超出部分每千克![]() 元.
元.
某人两次到该店购买这种水果的数量![]() (千克)与付款
(千克)与付款![]() (元)如下表:
(元)如下表:
| 付款 |
|
|
| 水果重量 |
|
|
(1)求![]() ,
,![]() 的值,并写出当
的值,并写出当![]() 和
和![]() 时,
时,![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)若购买这种水果![]() 千克,应付款多少元?
千克,应付款多少元?
26.(本小题满分10分)
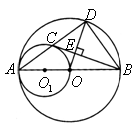 如图,已知
如图,已知![]() 为
为![]() 的直径,
的直径,![]() 以
以![]() 为直径,
为直径,![]() 的弦
的弦![]() 交
交![]() 于点
于点![]() ,
,![]() 于点
于点![]() .
.
(1)求证:![]() 为
为![]() 的切线;
的切线;
(2)若![]() ,求
,求![]() 的半径及
的半径及![]() 的长.
的长.
27.(本小题满分12分)
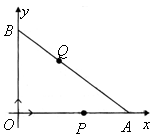
如图,在平面直角坐标系中,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() .点
.点![]() ,点
,点![]() 同时从原点出发作匀速运动,点
同时从原点出发作匀速运动,点![]() 沿
沿![]() 轴正方向运动,点
轴正方向运动,点![]() 沿
沿![]() 方向运动,并同时到达点
方向运动,并同时到达点![]() .点
.点![]() 运动的速度为
运动的速度为![]() 厘米/秒.
厘米/秒.
(1)求点![]() 运动的速度;
运动的速度;
(2)当点![]() 运动到线段
运动到线段![]() 上时,设点
上时,设点![]() 运动的时间为
运动的时间为![]() (秒),
(秒),![]() 的面积为
的面积为![]() (平方厘米),那么用
(平方厘米),那么用![]() 的代数式表示
的代数式表示![]() _____________;并求
_____________;并求![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)若将(2)中所得函数的自变量![]() 的取值范围扩大到任意实数后,其函数图象上是否存在点
的取值范围扩大到任意实数后,其函数图象上是否存在点![]() ,使得点
,使得点![]() 与该函数图象和
与该函数图象和![]() 轴的两个交点所组成的三角形面积等于
轴的两个交点所组成的三角形面积等于![]() 的面积?若存在,求出点
的面积?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
 |